1. 引言
对流扩散方程是一类重要的模型方程,在流体力学数值计算中有着重要的意义。对流扩散方程中对流项是描述流体流动过程的物理量,可以用关于空间的一阶导数来表示。对流项的数值计算在流体数值计算中起着重要的作用。数值格式离散对流项时要求在解的光滑区域具有较高的精度,在大梯度附近稳定且有界,关系到对流扩散方程数值解的精度、稳定性和收敛性。因此,对流项的数值格式的研究对减少数值解过度耗散起着关键作用。
目前已经提出了很多经典的低阶数值格式,例如一阶迎风格式FOU (First-Order Upwind)和Lax- Friedrichs格式[1] ,但是这些格式会产生数值耗散。为了弥补这一不足,人们又提出了高阶数值格式,例如,中心差分格式CD (Central Difference)、二阶迎风SOU (Second-Order Upwind)、Lax-Wendroff [2] 、QUICK (Quadratic Upstream Interpolation for Convective Kinematics) [3] 和CUI (Cubic Upwind Interpolation)格式 [4] 。但是,根据Godunov [5] 中的结论,高阶格式(High-Order Scheme)对于对流项的离散,不满足有界性,会造成间断解的非物理震荡。因此,如何消减数值耗散仍是一项极具挑战性的任务。
针对上述问题,人们提出了高分辨率格式(High Resolution Scheme) [6] [7] 。高分辨率格式是高阶格式与某些有界性准则的结合,它能很好地解决间断解的问题,消除数值解的非物理震荡。高分辨率早期的相关研究就是利用Harten提出的TVD (Total Variational Diminishing Constraint)性质构造一个通量限制函数,然后将它和高阶格式结合形成高分辨格式 [6] 。另外一个重要的构造高分辨率格式是结合Leonard提出的NVF (Normalized Variable Formulation)方法 [8] 与Gaskell和Lau [1] 提出的CBC (Convection Boundness Criterion)准则,格式离散对流项时,需要计算界面值,用到相邻的三个节点值,如图1所示,CBC准则能控制对流项的界面插值位于两相邻节点值之间,使得格式局部有界。在此基础上,出现了不同的高分辨率格式,如SMART [9] 、MUSCL [10] 和HOAB格式 [11] 等。在科学计算和工程应用上,利用这些高分辨率格式,人们已经取得了较理想的数值计算格式和模拟结果。

Figure 1. Three neighboring mesh points and the mesh face
图1. 三个相邻结点及单位边界
本文通过利用Newton插值多项式的方法结合TVD和CBC-BAIR条件构造了一个全新的高分辨率格式(NPUS),并且利用这一新格式进行了数值模拟及计算。本文安排如下:第二节介绍对流有界性准则;第三节建立对流项的高分辨率格式;第四节给出时间离散方法;第五节给出典型算例及计算结果讨论;第六节得出结论。
2. 对流有界性准则
经典的高分辨格式大都是通过将某种对流有界性准则与高阶格式结合而得到的。而高阶格式是通过对 格式的赋值得到的。
格式的赋值得到的。 格式公式化后为:
格式公式化后为:
 (2.1)
(2.1)
其中,参数的范围为 ,赋予
,赋予 不同的值就可以得到一些不同的高阶格式。根据Leonard [2] 中的思想,将初始变量
不同的值就可以得到一些不同的高阶格式。根据Leonard [2] 中的思想,将初始变量 转化到标准的格式下,我们通常在重构步中选取界面处相邻的控制单元。正则化过程可以写为
转化到标准的格式下,我们通常在重构步中选取界面处相邻的控制单元。正则化过程可以写为
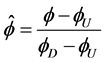
则 格式(2.1)可以正则化为
格式(2.1)可以正则化为
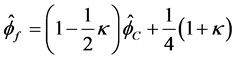
这表明正则变量 的变化只依赖于
的变化只依赖于 和
和 。
。
在数值求解过程中,对流项的处理要求在解的光滑区域具有较高的精度,在激波或大梯度附近稳定且有界。根据Godunov的结论 [5] ,传统高阶数值格式对于对流项的离散,不满足有界性,容易产生非物理震荡。线性对流格式及其NV形式如表1所示。因此想要消除震荡,必须将有界性准则和高阶格式结合构成高分辨格式来离散对流项。Gaskell和Lau [1] 利用NVF构造了对流有界性准则CBC,在NVF形式下CBC可以写为
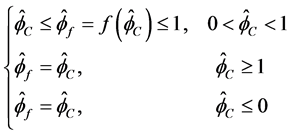

Table 1. The linear convection schemes and the NV formulations
表1. 线性对流格式及其NV形式
由于CBC准则对于格式的精度没有保证,为此Yu等人 [12] 和Hou等人 [13] 进一步提出了BAIR准则

另外,TVD格式的NVF形式为
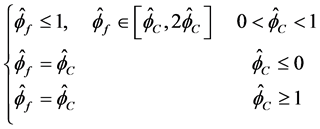
图2中的重叠阴影部分为TVD条件和BAIR条件的重合区域。如果一个数值格式的NVF曲线落入此重叠区域,就意味着此格式同时满足TVD和BAIR条件,则数值格式具有对流有界性。
3. 格式的构造
根据HR格式的标准化形式: 。在图2中,所构造的高分辨率有限体积格式的NV线必须落在TVD、CBC和BAIR的交集阴影区域内,才能满足对流有界性。则:
。在图2中,所构造的高分辨率有限体积格式的NV线必须落在TVD、CBC和BAIR的交集阴影区域内,才能满足对流有界性。则:
1) 由图2可知 ;
;
2) ,参数的范围为
,参数的范围为 而且
而且 。
。
这样可以保证格式满足TVD和BAIR等准则,本文中令 。选取
。选取 和
和 是因
是因
为这两个点是CBC、TVD和BAIR的NV线边界的交点值,控制这两个点的取值能更好地防止格式的落在阴影区域的外部。根据以上的条件,我们利用五点的Newton插值多项式可以构造出格式
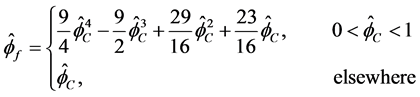
图3中红色的曲线为构造的NPUS格式在NVF意义下的曲线。通过图3可以看出,格式很好地满足CBC、TVD、BAIR等准则。
4. 时间离散格式
经过对空间离散之后,我们可以得到关于时间 的常微分方程。对于该常微分方程的求解主要有两种方法:第一种是Lax-Wendroff型方法,即对时间
的常微分方程。对于该常微分方程的求解主要有两种方法:第一种是Lax-Wendroff型方法,即对时间 进行Talyor展开,然后利用原PDE把时间导数转换成空间导数,再离散这些空间导数。但对多维问题这种时间离散方法太复杂。第二种方法是利用通常的ODE方法,如Runge-Kutta方法或多步方法,这是有限体积方法主要采取的时间离散方法,特别是Shu所提出的TVD型Runge-Kutta时间离散方法,对于间断解和稳定的空间离散组合是非线性稳定的 [14] 。
进行Talyor展开,然后利用原PDE把时间导数转换成空间导数,再离散这些空间导数。但对多维问题这种时间离散方法太复杂。第二种方法是利用通常的ODE方法,如Runge-Kutta方法或多步方法,这是有限体积方法主要采取的时间离散方法,特别是Shu所提出的TVD型Runge-Kutta时间离散方法,对于间断解和稳定的空间离散组合是非线性稳定的 [14] 。
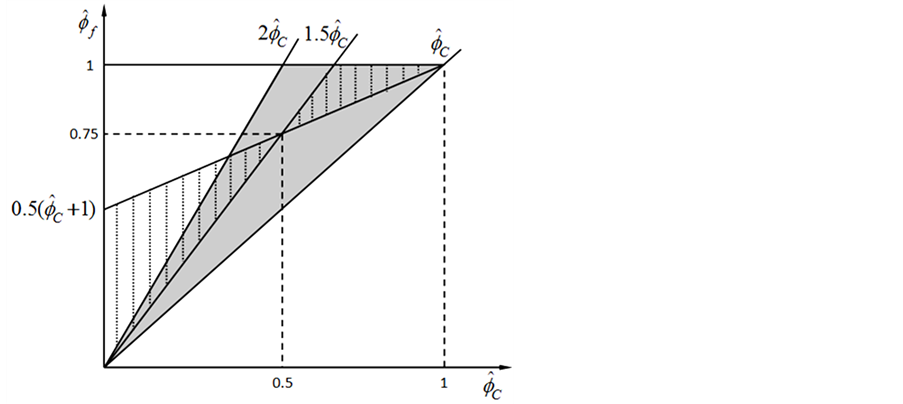
Figure 2. The regions of the TVD (shaded) and BAIR (hatched)
图2. TVD条件和BAIR条件
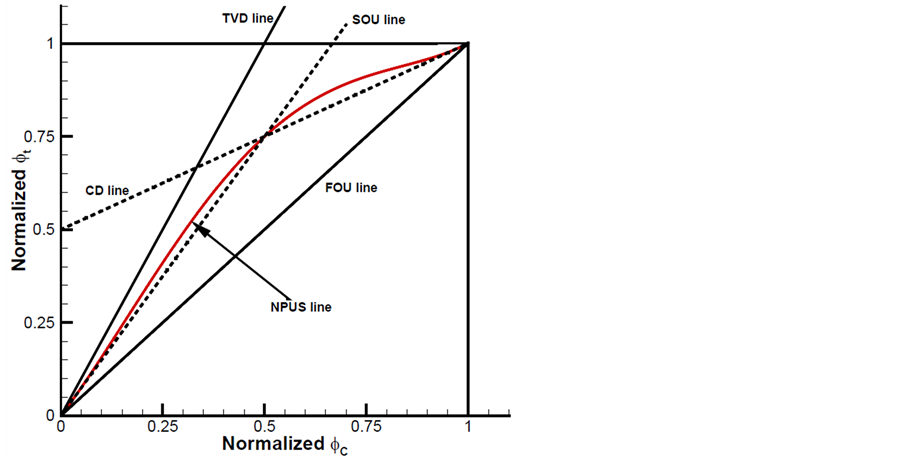
Figure 3. The NV line of the NPUS scheme in the BAIR and TVD region
图3. NPUS曲线与BAIR和TVD区域
二阶TVD型Runge-Kutta时间离散格式是:
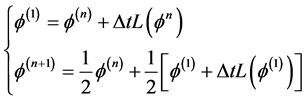
其中 是空间离散算子。
是空间离散算子。
5. 数值结果及讨论
为了更好地说明Newton插值条件下的高分辨率格式(NPUS)在离散对流项时所具有的性质,我们对以下算例进行了数值计算并与MUSCL格式进行了对比。数值计算过程中,选取了具有二阶精度的TVD二阶Runge-Kutta方法 [14] 且稳定性条件要求 。
。
5.1. 一维线性对流方程
线性对流方程为
 (5.1)
(5.1)
对于给定以下三中不同的初始条件得到相应的数值结果。
5.1.1. 情形1
给定初值条件为光滑初值条件 以及
以及 时,求解方程(5.1)得到的数值解。格式的精度计算公式为:
时,求解方程(5.1)得到的数值解。格式的精度计算公式为:

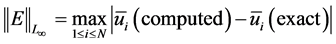
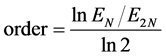
在区间[−1, 1]上求解方程(5.1),CFL选取0.5,通过计算NPUS格式,MUSCL格式及SMART格式在等距剖分20、40、80、60和320份的情形下数值解,利用上述的公式分别计算出 、
、 和
和 下的误差,同时得到数值精度阶(如表2)。
下的误差,同时得到数值精度阶(如表2)。
由表2,我们可以看到三个格式在 范数的意义下,都可以达到二阶精度。
范数的意义下,都可以达到二阶精度。
5.1.2. 情形2
同样对于上述简单的对流方程,依然选取速度为 使得标量
使得标量 沿着
沿着 以速度
以速度 移动。若选取初值为如下的非光滑初值条件
移动。若选取初值为如下的非光滑初值条件

Table 2. Errors and orders for several selected schemes
表2. 格式误差与数值精度阶对比
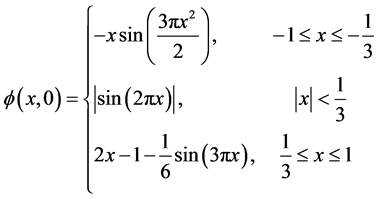
选取计算的区间为[−2, 2],且800等分,计算时间为T = 0.5,CFL条件选取0.2和0.5分别得到图4(a)和图4(b)。图4利用NPUS格式的结果对比于经典格式MUSCL在同样条件下的结果。图4中NPUS为牛顿插值下的高分辨率格式的结果。通过观察,我们发现NPUS格式与其余的二阶格式具有相近的逼近效果。
5.1.3. 情形3
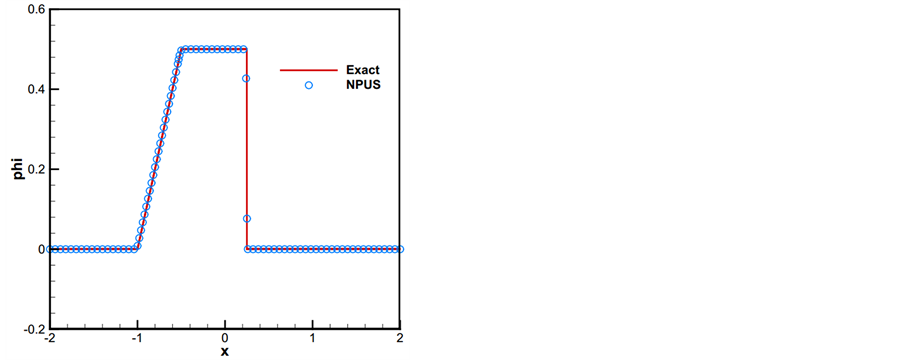
对于上述对流方程,选取如下的非光滑初值条件

该初值为W形的间断方波。计算过程中将区间[−0.5, 2.5]剖分为800个区间,时间选取T = 1.0,图5(a)表示CFL = 0.2时MUSCL和NPUS格式数值结果的对比图。图5(b)中CFL = 0.5。
5.2. 一维非线性Burgers方程
本节,我们利用NPUS求解一维非线性的无粘性Burgers方程,对于带有粘性的方程:
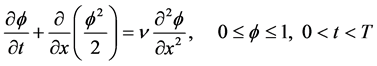
当 时,方程会产生光滑解。当
时,方程会产生光滑解。当 ,方程会的解会出现非物理震荡。所以,如果令
,方程会的解会出现非物理震荡。所以,如果令 ,方程为
,方程为
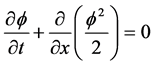
5.2.1. 情形1
首先,我们选取光滑的初始条件:

 (a) CFL = 0.2, T = 0.5, N = 800 (b) CFL = 0.5, T = 0.5, N = 800
(a) CFL = 0.2, T = 0.5, N = 800 (b) CFL = 0.5, T = 0.5, N = 800
Figure 4. Comparison of MUSCL and NPUS scheme for the linear equation with nonsmooth initial distribution
图4. 非光滑初值条件1:MUSCL与NPUS对比

 (a) CFL = 0.2, T = 1.0, N = 800 (b) CFL = 0.5, T = 1.0, N = 800
(a) CFL = 0.2, T = 1.0, N = 800 (b) CFL = 0.5, T = 1.0, N = 800
Figure 5. Comparison of MUSCL and NPUS scheme for the linear equation with nonsmooth initial distribution
图5. 非光滑初值条件2:MUSCL与NPUS对比
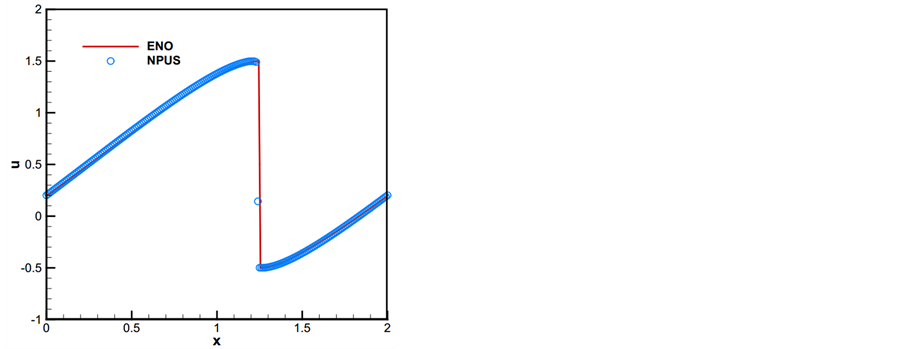
Figure 6. One-dimensional inviscid Burgers equation: comparison of the numerical solutions by the NPUS with 400 cells at CEL = 0.5 with the exact solution
图6. 一维无粘性Burgers方程光滑初值条件NPUS的数值解CFL = 0.5, N = 400
5.2.2. 情形2
初值条件为非光滑的无粘性Burgers方程,选取如下的初值条件进行模拟:
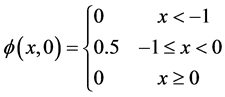
计算区间为 ,并400等分。由于无粘性Burgers方程的特性,在上述初值的条件下,选取T = 1.0得到图7(a)和图7(b),选取T = 2.0得到图7(c)和图7(d)。为了更好的分析格式对该类问题的求解,选取CFL = 0.2得到图7(a)和图7(c)、CFL = 0.5得到图7(b)和图7(d)。从图中可以看到对于间断处,格式NPUS能够有效地抑制震荡的产生,并且对于精确解有较好的逼近效果。
,并400等分。由于无粘性Burgers方程的特性,在上述初值的条件下,选取T = 1.0得到图7(a)和图7(b),选取T = 2.0得到图7(c)和图7(d)。为了更好的分析格式对该类问题的求解,选取CFL = 0.2得到图7(a)和图7(c)、CFL = 0.5得到图7(b)和图7(d)。从图中可以看到对于间断处,格式NPUS能够有效地抑制震荡的产生,并且对于精确解有较好的逼近效果。
5.3. 一维非线性Buckely-Leverett方程
一维情形下,非线性非凸的标量Buckely-Leverett方程形式如下

初始条件为
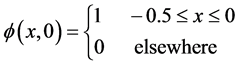
选取常CFL = 0.5,时间步长 ,并将区间
,并将区间 等分为400份。利用ENO格式可
等分为400份。利用ENO格式可
以得到该方程在上述初值条件下的数值解,如图8中的实线。我们利用格式NPUS数值计算该方程到时间为T = 0.4时,得到逼近结果如图8的圆圈。从图形可以看出:数值计算结果很好的逼近ENO格式的数值解,在大梯度附近很好地抑制震荡。
5.4. 二维线性对流方程
利用格式NPUS求解二维对流方程,我们选取Doswell问题的数学模型
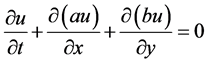
其中在速度场中有稳定的切向速度
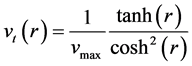
在计算中 ,而且在该场中
,而且在该场中
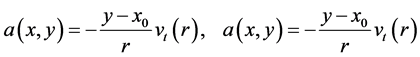
其中 为旋转中心,
为旋转中心, 表示区域内任意一点与中心的距离。定义角速度为
表示区域内任意一点与中心的距离。定义角速度为 。计算时我们选取计算区域为
。计算时我们选取计算区域为 的方形区域内。该问题的精确解
的方形区域内。该问题的精确解
 (a) CFL = 0.2, T = 1.0, N = 400 (b) CFL = 0.5, T = 1.0, N = 400
(a) CFL = 0.2, T = 1.0, N = 400 (b) CFL = 0.5, T = 1.0, N = 400
 (c) CFL = 0.2, T = 2.0, N = 400 (d) CFL = 0.5, T = 2.0, N = 400
(c) CFL = 0.2, T = 2.0, N = 400 (d) CFL = 0.5, T = 2.0, N = 400
Figure 7. One-dimensional inviscid Burgers equation with nonsmooth initial distribution: comparison of the numerical solutions by the NPUS with the exact solution
图7. 一维无粘性Burgers方程非光滑初值条件NPUS数值解
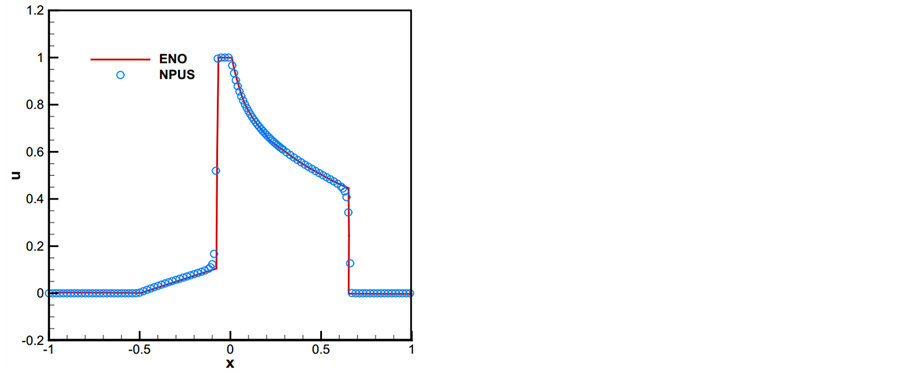
Figure 8. Comparison of numerical and exact results of the Buckley-Leverett equation
图8. 一维非线性Buckely-Leverett方程NPUS数值解
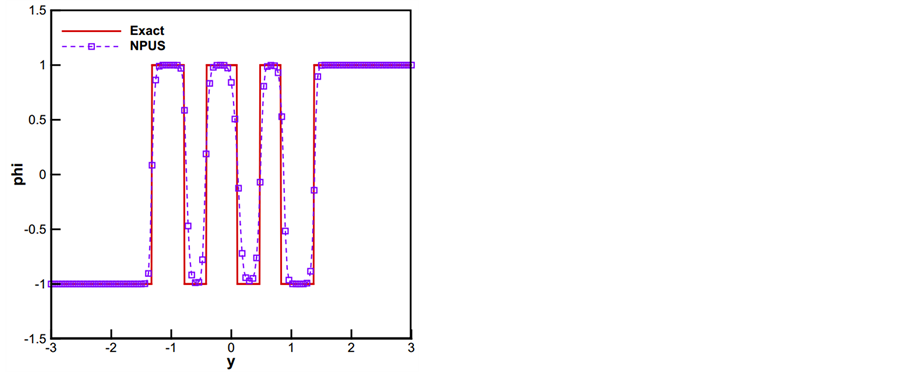
 (a) 1-D case: x = 0 (b) 2-D case
(a) 1-D case: x = 0 (b) 2-D case
Figure 9. Exact and numerical solutions of Doswell frontogenesis at t = 4. The meshes of 200 × 200 are used
图9. Doswell frontogenesis数值解 T = 4, N × N = 200 × 200
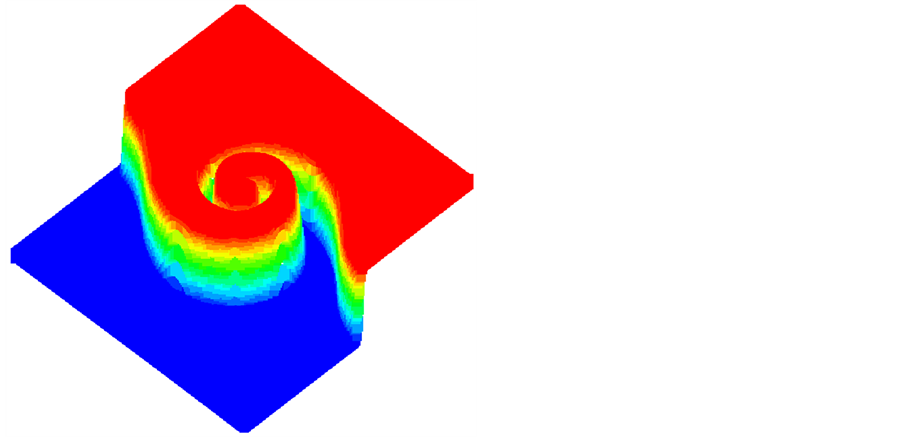
Figure 10. The numerical solution of Doswell frontogenesis in 3D view
图10. Doswell frontogenesis数值解3-D情形
参数 象征了锋面的梯度。初值条件可以令t = 0得到
象征了锋面的梯度。初值条件可以令t = 0得到 ,同时计算中选取
,同时计算中选取 。计算区域为[−3, 3] × [−3, 3],将其等距剖分为200 × 200的网格。CFL = 0.45的条件下,计算到时间T = 4,利用NPUS得到数值结果如图9所示。图9(a)是选取
。计算区域为[−3, 3] × [−3, 3],将其等距剖分为200 × 200的网格。CFL = 0.45的条件下,计算到时间T = 4,利用NPUS得到数值结果如图9所示。图9(a)是选取 时,数值解关于
时,数值解关于 的图像。图9(b)显示了数值解的2D图。由图9(a)可以清晰地看到NPUS格式能够很好的逼近精确解。图9(b)反应了锋面生成漩涡的形状。图10展示了数值解的三维图。
的图像。图9(b)显示了数值解的2D图。由图9(a)可以清晰地看到NPUS格式能够很好的逼近精确解。图9(b)反应了锋面生成漩涡的形状。图10展示了数值解的三维图。
6. 总结
本文以CBC (BAIR)准则为基础,通过结合TVD条件,在NVD下利用牛顿插值形式,构造高分辨率(NPUS)格式。此格式在离散对流项时计算方案简洁,多个经典算例表明,本文的计算格式具有较高的数值分辨率以及优良的计算稳定性。
致谢
本文由教育部科学技术研究重点项目(12024)与内蒙古自治区人才开发基金项目(12000-1300020240)支持。