1. 引言
一维Sine-Gordon方程是重要的非线性数学物理方程,可以用来描述流体力学、气象学、场论等领域很多物理现象。例如,传播中的磁通量子两个超导体之间的约瑟夫逊结[1] ,严格的钟摆的运动在拉伸线[2] 、固体物理、非线性光学、流体运动的稳定性。人们对此已经用一些方法作了研究。例如,显式有限差分格式和隐格式离散能量守恒方法[3] 。Strauss and Vázquez [4] ,使用经典的有限差分格式[5] [6] ,计算了Klein-Gordon方程。而[7] 的作者提出了一个使用基函数的方法。Ramos [8] 使用五点隐式有限差分方法。[9] 提出了一种通用的解决Sine-Gordon方程的辛方法。Batiha et al. [10] 给出了一个变分迭代法来获得Sine-Gordon方程的近似解。[11] 是将Sine-Gordon方程转化为一阶非线性初值问题,然后利用递归矩阵在时间和空间近似的二阶方法。Bratsos [12] 提出了一种二阶的空间精度和四阶的时间精度的方法。
在本文中,我们利用紧致四阶有限体积方法离散空间导数,用稳定的三阶Runge-Kutta方法求解一阶常微分方程组。文章框架如下,第一节为引言。第二节构造求解Sine-Gordon方程所使用的4阶紧致有限体积方法。第三节给出时间离散方法,即Runge-Kutta方法;第四节两个典型算例及计算结果讨论。
一维Sine-Gordon方程如下:
 (1)
(1)
初始条件为
 (2)
(2)
边界条件为
 (3)
(3)
为了方便研究能量守恒关系,代入
 (4)
(4)
其中 是一个常数,那么方程(1)可以变化为非线性常微分方程
是一个常数,那么方程(1)可以变化为非线性常微分方程
 (5)
(5)
由文献[1] 可知,方程(1)的非平凡解为
 (6)
(6)
我们常用孤立子方程的守恒性质来检验对方程数值离散的精度[13] 。一个具体的孤立子波的能量表达式为
 (7)
(7)
2. 紧致有限体积方法
考虑计算区域为 ,将其剖分成
,将其剖分成 个区域,那么共有
个区域,那么共有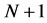 个结点,每个小区间的长度为
个结点,每个小区间的长度为

对(1)式在第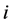 个小区间单元上对上式求积分,并对等式两边同时除以
个小区间单元上对上式求积分,并对等式两边同时除以 ,可以得到
,可以得到
 (8)
(8)
记 ,称
,称 为
为 在第
在第 个单元上的单元平均值,那么(8)式可以简记为
个单元上的单元平均值,那么(8)式可以简记为

首先,要对上式 、
、 进行估计,通过参考文献我们可以得到如下的估计式
进行估计,通过参考文献我们可以得到如下的估计式
 (9)
(9)
对应4阶精度的系数为[14]
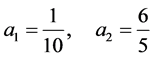
这些系数的确定,可以通过在点 泰勒展开得到,例如
泰勒展开得到,例如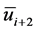 在点
在点 的泰勒展开为
的泰勒展开为

并且在Sine-Gordon方程中对应的边界条件为Dirichlet边界条件,那么对应的左边界处格式为
 (10)
(10)
通过Taylor展开计算出对应的系数为
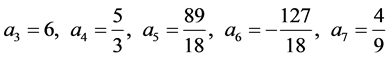
相应的右边界格式只是左边界格式的一个镜面映射。令

那么可以得到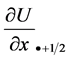 和
和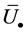 之间的关系如下
之间的关系如下
 (11)
(11)

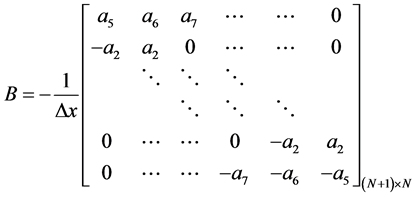 ,
, 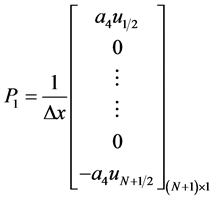
这样,我们就可以得到关于一阶导数离散格式为
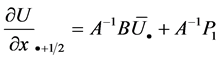 (12)
(12)
对于右端项的非线性项,我们选取了常用的辛普森公式近似计算其定积分
 (13)
(13)
此时仍需要对上式中的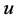 利用单元平均值进行近似。对于
利用单元平均值进行近似。对于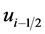 和
和 可以利用下面的格式近似
可以利用下面的格式近似
 (14)
(14)
其中4阶格式的相应系数为[14]

对于Dirichlet边界条件,该格式也可以直接应用。下面令

那么在对于空间离散的过程中,可以得到 和
和 之间的关系,如下
之间的关系,如下

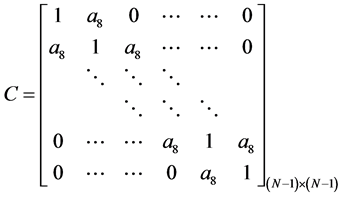 ,
,  ,
, 
得到空间离散格式为
 (15)
(15)
这样就将数值积分中的单元边界值处理完毕。下面要解决 在
在 点的数值近似,其中一种方法就是利用上文已经处理的单元边界值对其进行近似,从而得到一个4阶数值近似格式
点的数值近似,其中一种方法就是利用上文已经处理的单元边界值对其进行近似,从而得到一个4阶数值近似格式
 (16)
(16)
对应的Dirichlet边界条件的左边界格式为
 (17)
(17)
对应的系数为

右边界也是类似的格式。我们令


那么可以得到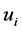 和
和 之间的关系,如下
之间的关系,如下

 ,
, 
这样就可以得到空间离散格式为
 (18)
(18)
将整个离散后的右端项记为 ,就有
,就有 ,这是一个常微分方程,从而空间离散完成。
,这是一个常微分方程,从而空间离散完成。
3. Runge-Kutta时间离散
在将右端项进行空间半离散之后,再考虑初始条件和边界条件,用3阶强稳定Runge-Kutta (a third- order strong stability preserving Runge-Kutta,即SSP-RK3)方法进行下一步处理。3阶的SSP-RK3的一般形式为[15]
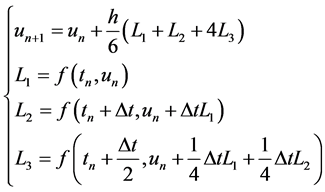 (19)
(19)
对于Sine-Gordon方程,需要将其转换成一阶常微分方程组,再用Runge-Kutta方法进行时间离散。如下

R,P分别定义为空间上的线性和非线性的微分算符。时间格式的选取依赖于所要的精度阶,要考虑储存、计算、稳定性。尤其是当R,P是非线性的时候,更没有依据说明全离散后的格式是稳定的,这时就更需要强稳定时间格式,常见的高阶稳定离散可见[16] 。
2阶方程对应初值问题的一般形式为

引进变量 ,可化为1阶方程组的初值问题
,可化为1阶方程组的初值问题
 (20)
(20)
(20)式对应的Runge-Kutta格式为

 (21)
(21)
4. 数值算例
例1:考虑如下的一维sine-Gordon方程
 (22)
(22)
将其改写为1阶方程组
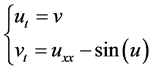
该方程的精确解为 [17]

通过下列的范数定义来计算所得的格式误差收敛阶,记

精度阶计算公式为

在区间[−6,6]上求解方程(22),取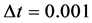 ,
, ,
, (见表1)。图1为在
(见表1)。图1为在 的时候精确解和数值解的曲线拟合情况。可以看到在不同的范数意义下,阶数都达到了4阶左右,从图像和误差上,都能看出准确解和数值解有着较好的吻合程度。
的时候精确解和数值解的曲线拟合情况。可以看到在不同的范数意义下,阶数都达到了4阶左右,从图像和误差上,都能看出准确解和数值解有着较好的吻合程度。
例2:一维sine-Gordon方程
 (23)
(23)
精确解为


Table 1. Errors and orders for 4-order CFVM
表1. 4阶紧致有限体积方法下的误差和精度阶

Figure 1. Curve: numerical and exact solution of the first experiment numerical (square); exact (solid line)
图1. 例1数值解和精确解的比较

Table 2. Errors and orders for 4-order CFVM
表2. 4阶紧致有限体积方法下的误差和精度阶

Figure 2. Curve: numerical and exact solution of the second experiment numerical (square); exact (solid line)
图2. 例2数值解和精确解的曲线拟合
在区间[−6,6]上求解方程(24),取 ,
,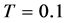 (见表2),在
(见表2),在 的时候精确解和数值解的曲线拟合情况(如图2)。从图像和误差上,准确解和数值解有着较好的吻合程度。因为初值条件相对于例1较为简单,从而在误差和精度阶上有着更好的结果。
的时候精确解和数值解的曲线拟合情况(如图2)。从图像和误差上,准确解和数值解有着较好的吻合程度。因为初值条件相对于例1较为简单,从而在误差和精度阶上有着更好的结果。
基金项目
本文由教育部科学技术研究重点项目(12024),内蒙古自治区人才开发基金项目(12000-1300020240)和内蒙古自然科学基金(2015MS0101)支持。