1. 引言
理论和实验是分不开的,彼此相互联系,现实中有很多不能用科学技术马上解决的实际问题,只有通过数值模拟得到实际应用所需要的数值结果,揭示其本质规律,从而来解决实际问题[1] [2] 。数值模拟在各门自然科学(物理学、气象学、地质学和生命科学)和技术科学与工程科学(核技术、航空航天和打下土木工程等等)中起着巨大的作用,在很多重要的领域成为不可缺少的工具。而科学与工程计算中最重要的内容就是求解在科学研究和工程技术中出现的各种各样的偏微分方程或方程组,而有限元方法就是在解决这些问题的基础上产生的[2] [3] 。
有限元法(finite element method)是一种高效能、常用的计算方法。有限元法是一种基于变分原理的方法,它适合于较复杂的区域和不同粗细的网格,正是具有这些特性,20世纪60年代以来,有限元方法的理论和应用得到迅速的发展,所以它广泛地应用于以拉普拉斯方程和泊松方程等偏微分方程所描述的各类物理现象之中[4] 。
本文正是通过偏微分方程中的对流扩散方程的有限元方法来如何模拟实际的科学研究和工程技术中的一些问题。对流扩散方程被广泛地应用于许多自然现象的表达之中,例如水和大气中的污染物质浓度的扩散、海水盐度、流体流动与传热、电化学反应等,还应用于环境科学、能源开发、电子科技等[5] 。
一般的稳态对流扩散方程方程形式如下[6] :
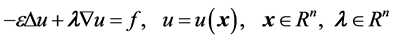 (1)
(1)
其中 为给定的常向量,(1)是n维稳态对流扩散方程,当n = 1时,我们得到:
为给定的常向量,(1)是n维稳态对流扩散方程,当n = 1时,我们得到:
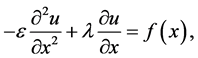 (2)
(2)
方程(2)是一维稳态对流扩散方程的一个基本形式,解决实际问题的时候还要加上边界条件才能模拟实际问题。因此对于方程(2),我们附加边界条件,于是得到对流扩散方程的边值问题:
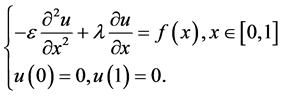 (3)
(3)
其中 为大于零的微小常数,
为大于零的微小常数, 为已知常数,方程(3)就是本文要研究的对流扩散方程,它是求解很多复杂微分问题的基础。并且小参数
为已知常数,方程(3)就是本文要研究的对流扩散方程,它是求解很多复杂微分问题的基础。并且小参数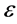 很小时会给一般的数值计算方法带来困难。
很小时会给一般的数值计算方法带来困难。
2. 有限元方法概述
常见的离散偏微分方程的数值方法有:有限元法、有限差分法和有限体积法。下面我们简单介绍有限元法的思想、有限元法的解题步骤。
2.1. 有限元法简介
有限元法(finite element method)的含义:有限元方法是一种高效能、常用的离散计算方法,它的基础是变分原理和加权余量法,选择特殊的基函数,其基本求解思想是把计算域划分为有限个互不重叠的单元,在每个单元内,选择一些合适的节点作为求解函数的插值点,将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式,借助于变分原理或加权余量法,将微分方程离散求解,从而使一个连续的无限自由度问题变成离散的有限自由度问题。有限元法有许多优点,包括适用于较一般的区域,也适用于较复杂的区域和不同粗细的网格,离散方程一般都满足积分守恒[5] [7] 。
2.2. 有限元法设计的基本思路
有限元法首先根据变分原理或方程余量与权函数正交化原理,建立与微分方程初边值问题等价的积分表达式[2] 。
对积分表达式,通过采用不同的权函数和插值函数形式,可构成不同的有限元法。有限元法有一鲜明特点:通常把计算域剖分为有限个互不重叠且相互连接的单元,再在每个单元内选择基函数,用单元基函数的线形组合来逼近未知函数在单元中的真解。如果整个计算域上总体的基函数可以由每个单元基函数组成,那么整个计算域内的解可以看作是由所有单元上的近似解构成。在有限元法中,单元基函数通过插值函数来构造。而插值函数分通常分为两大类,一类只要求插值多项式本身在插值点取已知值,称为拉格朗日多项式插值;另一种不仅要求插值多项式本身,还要求它的导数值在插值点取已知值,称为哈密特多项式插值[2] [3] [8] 。
2.3. 有限元方法的解题基本步骤 [4]
1) 通过变分原理将微分方程转化为变分形式的方程
2) 单元剖分:将待解区域进行分割,离散成有限个子区间的集合,每一个子区间就称为一个单元,单元的形状原则上可以是任意的,二维问题一般采用三角形单元或矩形单元,三维空间可采用四面体或多面体等,每个单元的顶点称为节点。
3) 有限元离散:在单元剖分的基础上,然后分割单元中任意点的未知函数用该分割单元中形状函数及离散网格点上的函数值展开,即建立一个插值函数,最后利用分段插值函数构造有限维子空间,通过它来离散变分形式的方程,构造有限元方程。
4) 求解近似变分方程:在前两部分的基础上最后进行约束处理,形成有限元法的代数方程组,再从该方程组求解函数在各节点上的近似值。
特别地,利用有限元法求解方程(3)的整个过程可用如下图示表示:
给定对流扩散方程边值问题→变分形式→有限元离散→代数方程组
3. 对流扩散问题变分化
我们先将对流扩散边值问题(3)转换为变分问题。
为了求解,在这里,我们先引入如下两个函数空间:
1)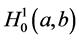 表示所有定义在区间[a,b]上具有一阶连续导数的函数;
表示所有定义在区间[a,b]上具有一阶连续导数的函数;
2) 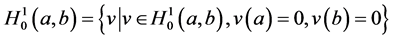
于是,利用变分法,求解关于方程(3)的边界问题就等价于下面形式的变分问题:
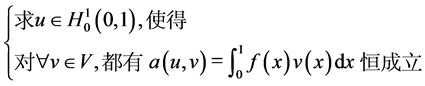 (4)
(4)
这里V表示 ,
,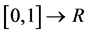 ,积分函数
,积分函数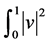 和
和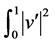 在边界条件
在边界条件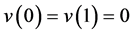 上有意义,我们要求解函空间数v,而a是定义在双线性空间
上有意义,我们要求解函空间数v,而a是定义在双线性空间 上的一个函数,具体表示如下:
上的一个函数,具体表示如下:
 (5)
(5)
可以证明:问题(4)的解正好是问题(3)的解,问题(3)的解正好是(4)的解。
为进一步离散变分问题(4),下面先做单元剖分:给定一正整数n,我们把区间[0,1]分成n + 1个子区间 。再对给定的正整数
。再对给定的正整数 ,我们假设
,我们假设 为定义在区间
为定义在区间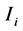 上的次数不超过
上的次数不超过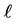 的多项式所形成的集合。
的多项式所形成的集合。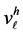 也是一定义在区间[0,1]上的函数组成的集合,图1是关于函数空间
也是一定义在区间[0,1]上的函数组成的集合,图1是关于函数空间 的两个实例。
的两个实例。
于是,有限元法是在 的条件下寻找近似的函数u,与(4)相比较,下面也是解决问题的一种方法:
的条件下寻找近似的函数u,与(4)相比较,下面也是解决问题的一种方法:
 (6)
(6)
在实际计算当中我们利用如下两个求积准则来离散变分问题(6):
1) 梯形法法(求积)准则:
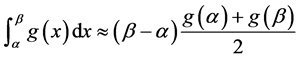 (7)
(7)
2) 辛普森正交法(求积)准则:
 (8)
(8)
对每个子区间 使用这些基本求积公式,我们得到一个在整个区间
使用这些基本求积公式,我们得到一个在整个区间 的求积公式。
的求积公式。
4. 两种有限元方法的求解过程
在本节中,我们设计两种不同的有限元法(FEM)来解决稳态对流–扩散问题,第一种方法是一次元(线性)法,记为P1,函数记为 ;第二种方法是二次元变分法,记为P2,函数近似空间记为
;第二种方法是二次元变分法,记为P2,函数近似空间记为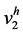 。
。
1) 基于一次元的有限元法,简记为P1,它在每个单元上用一次多项式来近似
当整数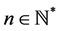 ,我们定义下列节点:
,我们定义下列节点:

定义间隔区间为:

网格比为 。给定整数k,我们可以定义帽子函数
。给定整数k,我们可以定义帽子函数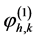 ,
, ,图2就是一个基本的帽子函数。
,图2就是一个基本的帽子函数。
其中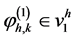 ,且
,且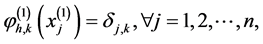 。
。
(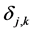 是Kronecker符号),需要注意的是
是Kronecker符号),需要注意的是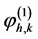 是作用于相连的两个区间
是作用于相连的两个区间 和
和 。在有限元方法中,点
。在有限元方法中,点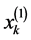 被称为节点,区间
被称为节点,区间 被称为单元格。
被称为单元格。
于是我们在 条件下,寻找近似的函数u,使其能在
条件下,寻找近似的函数u,使其能在 的情况下求解(6)。于是用这样的一次元,我们得到问题(6)变分问题的推论形式:
的情况下求解(6)。于是用这样的一次元,我们得到问题(6)变分问题的推论形式:
 (9)
(9)
因为 是函数空间
是函数空间 的一组基,我们可以用基
的一组基,我们可以用基 来代替(9)式中的
来代替(9)式中的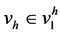 ,所以推论(9)等价于下面形式的变分问题:
,所以推论(9)等价于下面形式的变分问题:
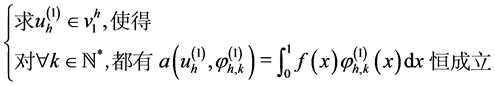 (10)
(10)
在 的基础上我们也可以展开函数
的基础上我们也可以展开函数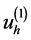 ,得到近似
,得到近似

这里 。当我们再定义向量
。当我们再定义向量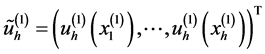 ,那么从方程(10),我们还可以得到:
,那么从方程(10),我们还可以得到:
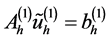 (11)
(11)
这里 是在
是在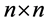 上的一个可逆的矩阵,它的基本元定义为:
上的一个可逆的矩阵,它的基本元定义为: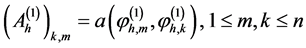 。
。 ,它是一个向量,它的每一个分量的定义如下:
,它是一个向量,它的每一个分量的定义如下: 。并且线性方程组(11)可以被分割成为下面这个矩阵方程:
。并且线性方程组(11)可以被分割成为下面这个矩阵方程:

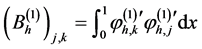 ,
, ,
,
其中 是对称三对角矩阵,
是对称三对角矩阵, 是反对称三对角矩阵。
是反对称三对角矩阵。
2) 基于一次元的有限元法,简记为P2,它在每个单元上用二次多项式来近似当整数 ,我们先定义下列节点:
,我们先定义下列节点:
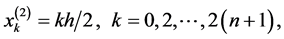
再定义单元区间为:
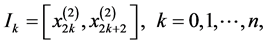
网格长度为:
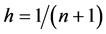 ,
,
这些定义都跟前面的有限元法P1相似,换句话说,在保持相同的数值间隔的同时,P2的不同是在每个间隔之间都添加一个中心节点,并将此节点取名为中心节点。采用P2的方法是为了得到更加精确的近似解。
我们在寻找在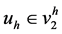 时,函数u的近似解,在
时,函数u的近似解,在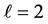 时有如下解决问题的方法:
时有如下解决问题的方法:
 (12)
(12)
(12)是我们建立 的基础。对于每一个单元格区间
的基础。对于每一个单元格区间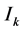 ,基于节点
,基于节点 ,
,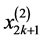 和
和 这三个相连点,我们定义如下三个二次拉格朗日多项式来联系:
这三个相连点,我们定义如下三个二次拉格朗日多项式来联系:
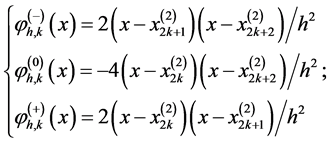 (13)
(13)
对于每一个节点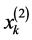 的网格,联系函数
的网格,联系函数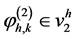 ,我们可以得到如下定义:
,我们可以得到如下定义:
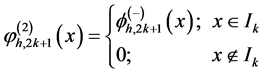

图3就是一个基本的实例。
根据奇偶校验观察k值变化,可以注意到函数 跟区间间隔
跟区间间隔 或者两个间隔的结合都没有关系,所以函数
或者两个间隔的结合都没有关系,所以函数 仅仅依赖于
仅仅依赖于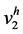 ,所以问题(12)就等价于下面这个变分问题:
,所以问题(12)就等价于下面这个变分问题:
 (14)
(14)
同样基于基函数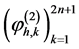 ,我们可以得到
,我们可以得到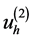 的一个展开:
的一个展开:

这里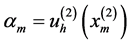 。再记向量
。再记向量 ,那么问题(14)可以化简为:
,那么问题(14)可以化简为:
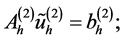 (15)
(15)
其中 是一个
是一个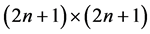 的矩阵,它的基本元定义为:
的矩阵,它的基本元定义为:

 是向量空间
是向量空间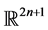 上的一个向量,它的基本元定义为:
上的一个向量,它的基本元定义为:
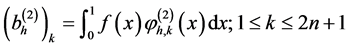
并且,线性方程组(16)之中的系数矩阵可以被分割成为下面这两个矩阵之和:

其中矩阵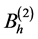 和
和 是五对角矩阵,与P1中一样,我们可以证明
是五对角矩阵,与P1中一样,我们可以证明 是正定的对称矩阵,
是正定的对称矩阵, 是反对称矩阵,而且矩阵
是反对称矩阵,而且矩阵 是可逆的。
是可逆的。
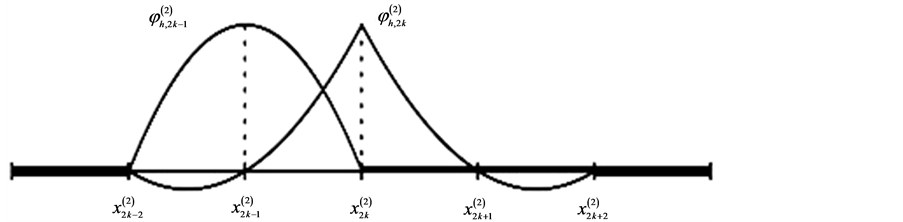
Figure 3. A hat function on Function Spaces 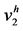
图3. 关于函数空间 的一个帽函数
的一个帽函数
5. 数值计算结果
在函数f为恒定常数的情况下,问题(2)具有如下解析解:

我们通过编写MATLAB程序计算未知函数u的一些离散点集,在定点条件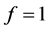 ,
, ,
,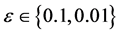 和
和 已知的情况下,画出函数
已知的情况下,画出函数 的精确解与近似解的图象,最后经过分析做出初步的结论。
的精确解与近似解的图象,最后经过分析做出初步的结论。
下面我们基于P1有限元法编写Matlab程序,先考虑 的情形。
的情形。
1) 当n = 10的情况下运行Matlab程序,其画图结果如图4;
2) 当n = 20的情况下运行Matlab程序,其画图结果如图5。
再考虑 的情形。
的情形。
1) 当n = 10的情况下运行Matlab程序,其画图结果如图6;
2) 当n = 20的情况下运行Matlab程序,其画图结果如图7。
这里的图4至图7是通过P1法计算得到的。通过计算结果我们可以发现:当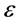 较大时(例如
较大时(例如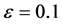 ),增大
),增大 的值(分别参见图4与图5),我们可以得到一个更好的近似解;当
的值(分别参见图4与图5),我们可以得到一个更好的近似解;当 较小时(例如
较小时(例如 ),虽然增大
),虽然增大 的值(分别参见图6与图7),我们并不能得到一个更好的近似解。原因在于在x = 1附近有一边界层(boundary layer),它给一般的数值离散方法(包括有限元法)带来困难。可以预见,当
的值(分别参见图6与图7),我们并不能得到一个更好的近似解。原因在于在x = 1附近有一边界层(boundary layer),它给一般的数值离散方法(包括有限元法)带来困难。可以预见,当 的数值(比如在区间[0.005, 0.02]变化)变得更小时,x = 1附近的边界层会给计算带来更大的困难。
的数值(比如在区间[0.005, 0.02]变化)变得更小时,x = 1附近的边界层会给计算带来更大的困难。
其次,我们基于P2有限元法编写Matlab程序,先考虑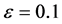 的情形。
的情形。
1) 当n = 10的情况下运行Matlab程序,其画图结果如图8;
2) 当n = 20的情况下运行Matlab程序,其画图结果如图9。
再考虑 的情形。
的情形。
1) 当n = 10的情况下运行Matlab程序,其画图结果如图10;
2) 当n = 20的情况下运行Matlab程序,其画图结果如图11。
这里的图8至图11是通过P2有限元法计算得到的。通过计算结果我们发现:当 较大时(例如
较大时(例如 ),增大
),增大 的值(分别参见图8与图9),我们可以得到一个更好的近似解;当
的值(分别参见图8与图9),我们可以得到一个更好的近似解;当 较小时(例如
较小时(例如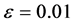 ),虽然增大
),虽然增大 的值(分别参见图10与图11),我们虽然得到一个较好的近似解(相对于一次有限元),但是依然有误差。原因同样在于在x = 1附近有一边界层。我们还同样可以预见,当
的值(分别参见图10与图11),我们虽然得到一个较好的近似解(相对于一次有限元),但是依然有误差。原因同样在于在x = 1附近有一边界层。我们还同样可以预见,当 的数值(比如在区间[0.005, 0.02]变化)变得更小时,x = 1附近的边界层会带来更大的计算误差。
的数值(比如在区间[0.005, 0.02]变化)变得更小时,x = 1附近的边界层会带来更大的计算误差。
6. 方法的改进
从上面计算分析可以看出:1) 两种有限元法在求解微分方程边值问题时的求解思路大致相同,P1有限元法是基于线性插值多项式得到的求解方法,P2有限元法基于是二次拉格朗日插值多项式得到的求解方法;2) 在间隔区间[0, 1]上,其他条件不变得情况下,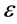 值从
值从 ,函数
,函数 的值在x = 1处有一边界层。当有边界层时,有限元法得到的近似解与精确解的误差较大(在x = 1附近)。
的值在x = 1处有一边界层。当有边界层时,有限元法得到的近似解与精确解的误差较大(在x = 1附近)。
我们注意到,在前面几节中所采用的有限元法(P1与P2)中,所用的小区间长度都是相等的(h = 1/10或1/20),它们是基于均匀网格得到的。为使得P1与P2这两种有限元法能够处理此类含有边界层的问题,建议采用基于非均匀网格的有限元法(nonuniform finite element method),这样做可更好地得到边界层附近的近似值。基于非均匀网格的有限元法可以在边界层(x = 1处)增加节点:例如在区间[0, 0.8]附近取h = 1/10,
在区间[0.8, 1]附近取h = 1/40;或者在区间[0, 0.8]附近取h = 1/20,在区间[0.8, 1]附近取h = 1/80;我们注意到,基于非均匀网格的有限元法算法求解过程与传统的有限元法大致相同,因而在编写程序时,并不会遇到更大的困难。
7. 总结
在本文中,我们研究了两种有限元法(P1与P2)求解稳态对流扩散方程边值问题的方法,并给出详细的算法过程与数值计算结果。这里P1是基于线性插值多项式得到的求解方法,P2基于是二次拉格朗日插值多项式得到的求解方法。我们发现当稳态对流扩散方程边值问题之中的微小元变得很小时,在端点附近会有一边界层。边界层的出现会给有限元计算带来较大的误差。为解决此问题,我们建议采用基于非均匀网格的有限元法,它是一种能求解含边界层的问题的高效数值方法。
致谢
本文受到云南省科技厅中青年学术带头人后备人才基金、教育部新世纪优秀人才基金与国家自然科学基金(11261065)等资助。