1. 引言
实际应用中的许多数学物理边值问题都能转化为积分方程来解决 [1] - [3] ,本文研究下列非线性第二类Hammerstein积分方程
 (1)
(1)
其中核函数 和
和 及自由项
及自由项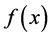 是已知函数,
是已知函数, 是待求的未知函数。对于具体的问题和背景,它们都有非常清晰的物理意义,所以找到求解第二类Hammerstein积分方程的数值解法显得十分必要。尽管求解Hammerstein积分方程的方法种类繁多,如Sinc-Collocation方法 [4] ,退化核方法 [5] ,Toeplitz Matrix方法 [6] 。常用的方法还有迭代法、Galerkin法、级数法和正交展开法等 [7] [8] ,由于非线性Hammerstein方程的求解方法有着重要的应用前景,其有效的数值解法一直是一个活跃的研究课题。
是待求的未知函数。对于具体的问题和背景,它们都有非常清晰的物理意义,所以找到求解第二类Hammerstein积分方程的数值解法显得十分必要。尽管求解Hammerstein积分方程的方法种类繁多,如Sinc-Collocation方法 [4] ,退化核方法 [5] ,Toeplitz Matrix方法 [6] 。常用的方法还有迭代法、Galerkin法、级数法和正交展开法等 [7] [8] ,由于非线性Hammerstein方程的求解方法有着重要的应用前景,其有效的数值解法一直是一个活跃的研究课题。
本文针对具有一般核函数的第二类Hammerstein积分方程给出一种新的数值解法,给出了数值解的收敛性和误差分析,最后举出数值实例说明该方法的可行性和有效性。
2. 新的数值方法
首先考虑方程(1)解的唯一性,在Banach空间上有下列定理:
定理1:假设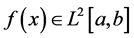 并且
并且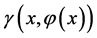 满足以下Lipschitz条件:
满足以下Lipschitz条件:
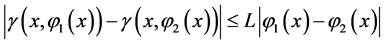 (2)
(2)
其中Lipschitz常数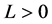 ,在以下约束条件:
,在以下约束条件:
 (3)
(3)
其中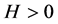 ,当
,当
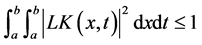 (4)
(4)
非线性积分方程(1)在 有唯一解。
有唯一解。
证明:因为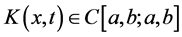 且
且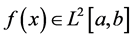 ,所以易知
,所以易知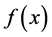 在
在 上有界,假设
上有界,假设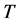 是一个算子且有
是一个算子且有 并且
并且 ,这里
,这里
 (5)
(5)
因为 ,易证
,易证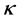 是
是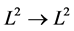 上的一个有界算子。
上的一个有界算子。
对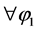 ,
, ,应用Lipschitz条件和Cauchy-Schwarz不等式有:
,应用Lipschitz条件和Cauchy-Schwarz不等式有:
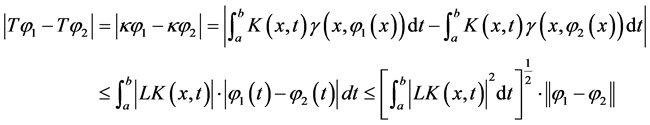 (6)
(6)
又因为
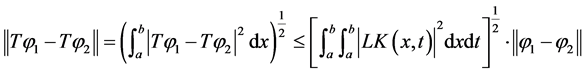 (7)
(7)
所以当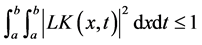 时,
时,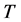 是一个压缩算子。故根据Banach空间上的不动点原理,易知
是一个压缩算子。故根据Banach空间上的不动点原理,易知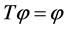 在
在 上有唯一解。
上有唯一解。
其次,采用积分中值定理和分段逼近的思想,我们给出一种新的数值方法。这里我们假设 ,
,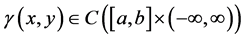 ,为了方便我们选取一系列等距分割点
,为了方便我们选取一系列等距分割点
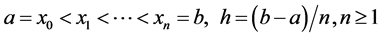
然后(1)式能改写成如下形式
 (8)
(8)
应用积分中值定理,(8)式能进一步写成
 (9)
(9)
这里 。通常
。通常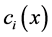 是关于
是关于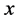 的函数,它是很难确定的,故在(9)式中我们用常数
的函数,它是很难确定的,故在(9)式中我们用常数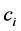 代替
代替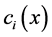 ,然后得到具有一般核的非线性第二类Hammerstein积分方程的近似解为
,然后得到具有一般核的非线性第二类Hammerstein积分方程的近似解为
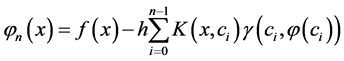 (10)
(10)
其中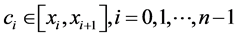 ,为了确定
,为了确定 和
和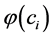 ,我们把(10)式代入到(1)式得到
,我们把(10)式代入到(1)式得到
 (11)
(11)
在(10)和(11)式中, 用
用 代,又会得到
代,又会得到
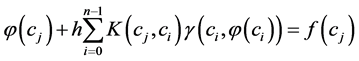 (12)
(12)
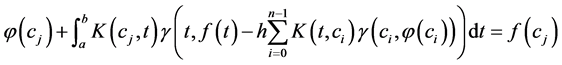 (13)
(13)
这样方程(12)和(13)形成一个关于 和
和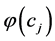 的非线性系统,它能用一些数值方法来求解,比如说复化辛普森方法、牛顿法等,一旦获得了非线性系统(12)和(13)的解,
的非线性系统,它能用一些数值方法来求解,比如说复化辛普森方法、牛顿法等,一旦获得了非线性系统(12)和(13)的解,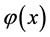 就能用(10)式表示出来。
就能用(10)式表示出来。
特别地,当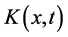 是退化核时,我们能给出非线性第二类Hammerstein积分方程(1)准确解的一种新方法。一般的,退化核
是退化核时,我们能给出非线性第二类Hammerstein积分方程(1)准确解的一种新方法。一般的,退化核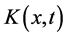 能表示成如下形式:
能表示成如下形式:
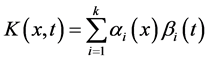 (14)
(14)
其中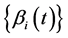 是一个线性无关的函数列,当
是一个线性无关的函数列,当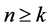 时,我们能得到方程(1)的准确解为:
时,我们能得到方程(1)的准确解为:
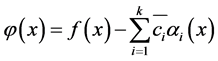 (15)
(15)
其中
 (16)
(16)
方程(9)能进一步表示成:
 (17)
(17)
从方程(15)和(17)中可以得出
 (18)
(18)
从而方程(18)形成一个含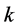 个方程和
个方程和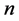 个未知函数
个未知函数 的系统,当
的系统,当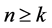 时,方程(18)总是可求解的,并且存在常数
时,方程(18)总是可求解的,并且存在常数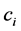 使得
使得
 (19)
(19)
从而准确解(17)能进一步写成:
 (20)
(20)
关于退化核的积分方程求解也显得非常重要的,因为一般核的积分方程可以采用退化核积分方程来逼近求解 [5] [8] 。
3. 近似解的收敛性和误差分析
下面分析近似解(10)的收敛性并进行误差估计。
定理2:若我们有以下的条件:
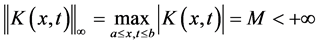 ,
,
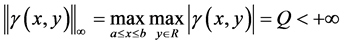 ,
,
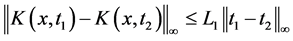 ,
,
 ,
,
其中 ,
, 和
和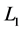 ,
,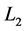 是常数,则有
是常数,则有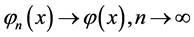 ,即
,即

且误差估计可写成如下形式:
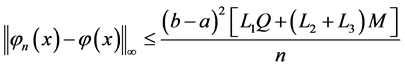 (22)
(22)
证明:从方程(9)和(10)中,我们可以得到:
 (23)
(23)
从(23)中很容易得出
 (24)
(24)
因此数值方法求得的近似解是收敛的。
4. 数值实例
本节通过几个数值实例验证方法的有效性。
例1:考虑以下的线性积分方程 [9] [10] :
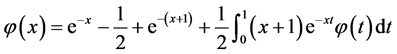
这里 ,准确解为
,准确解为 。基于新的数值方法,其近似解和准确解的绝对误差如下表1所示。
。基于新的数值方法,其近似解和准确解的绝对误差如下表1所示。
其中T和S分别表示使用复化的Trapezoid方法和复化的Simpson方法在 [10] 中求的结果。从表1中可以看出,本文方法得到的近似解和准确解的绝对误差的收敛速度更快,比 [9] 和 [10] 中的数值结果更精确。当 增大时,
增大时, 的绝对误差逐渐减小,所得的近似解很好的符合了定理2的分析。
的绝对误差逐渐减小,所得的近似解很好的符合了定理2的分析。
例2:考虑具有退化核的Hammerstein积分方程 [11] - [13] :
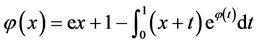
这里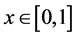 ,准确解为
,准确解为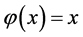 。当
。当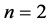 时,使用本文方法有:
时,使用本文方法有:
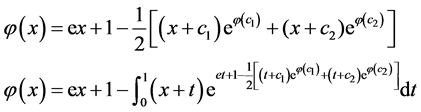

Table 1. The absolute errors of approximate and exact solutions for Example 1
表1. 关于例1的近似解和准确解的绝对误差
这里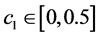 ,
, 。通过把
。通过把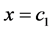 和
和 分别代入以上两个方程,经过计算后得到:
分别代入以上两个方程,经过计算后得到:
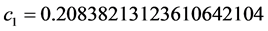 ,
,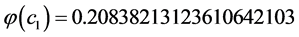
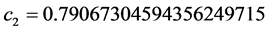 ,
,
因此 ,由于
,由于 ,故当
,故当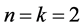 时,经过以上的计算我们便能得到准确解,这也很好的符合了核函数为退化核时的分析。把该例子计算得到的结果和在 [11] - [13] 中的结果进行比较后,能发现本文的新方法更简单。
时,经过以上的计算我们便能得到准确解,这也很好的符合了核函数为退化核时的分析。把该例子计算得到的结果和在 [11] - [13] 中的结果进行比较后,能发现本文的新方法更简单。
非线性积分方程的边值问题可以化为积分方程进行求解和分析,下面基于本文方法,举例说明非线性Duffing方程的三点边值问题数值求解的新方法。
例3:考虑下面Duffing方程的三点边值问题:
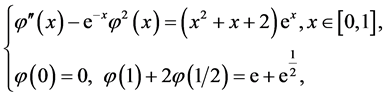
这里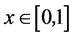 ,
,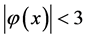 ,准确解为
,准确解为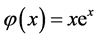 ,非线性边值问题可通过积分的方法化为如下等价的第二类Hammerstein积分方程
,非线性边值问题可通过积分的方法化为如下等价的第二类Hammerstein积分方程
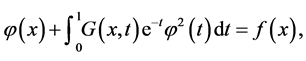
这里

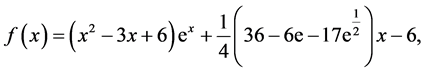
我们首先证明该Hammerstein积分方程解的唯一性,选择如下Lipschitz常数:

Table 2. The absolute errors of approximate and exact solutions for Example 3
表2. 关于例3的近似解和准确解的绝对误差
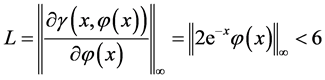
又因为:

即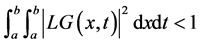 ,所以根据定理1可知该非线性三点边值问题有唯一解。使用本文的新方法求解此第二类Hammerstein积分方程,这里我们选择
,所以根据定理1可知该非线性三点边值问题有唯一解。使用本文的新方法求解此第二类Hammerstein积分方程,这里我们选择 分别进行计算,得到的近似解和准确解的绝对误差如上表2所示。从表格2中我们可以看到随着
分别进行计算,得到的近似解和准确解的绝对误差如上表2所示。从表格2中我们可以看到随着 的增大,近似解和准确解的绝对误差在逐渐减小,所得结果很好的符合了定理2的分析。
的增大,近似解和准确解的绝对误差在逐渐减小,所得结果很好的符合了定理2的分析。
5. 结语
本文给出了一种非线性Hammerstein积分方程数值解的新方法,分析了近似解的误差和收敛性。非线性Duffing方程的三点边值问题可以转为该类非线性Hammerstein积分方程。与已有的方法比较并通过数值计算表明本文方法简单和有效。
基金项目
本工作受国家自然科学基金项目(11362002),广西高校优秀中青年骨干教师培养工程项目和广西研究生教育创新计划项目(YCSZ2015030)经费支助。