1. 引言
十九世纪三十年代造船工程师John Scott Russell首次观察到了孤波,这也是人类历史上第一次观察到这种非常奇特的自然现象,随后Russell进行了一系列的实验并在1840年的报告中谈到他发现的孤波。在孤波的概念提出之后随即就引发了科学家的争论,直到1895年Diederik Johannes Korteweg和Gustav de Vries从流体动力学的角度得到浅水波方程(即KdV方程)和它的行波解,这场争论才得以结束,因为当KdV的行波解的波长趋于无限的时候,这个行波就变成了罗素所说的孤波,至此孤波这一概念才被学术界普遍接受。
再经过之后的60年的平静期之后,1955年,Enrico Fermi,John Pasta和Stan Ulam提出了著名的Fermi- Pasta-Ulam (FPU)问题,并且他们用MANIAC I计算机进行数值计算得到了出乎意料的结果:当系统运动充分长的时间之后并没有达到能量均分的状态,反而回到了系统的初始状态。为了解释和理解这个实验结果,1965年Martin D. Kruskal和Norman J. Zabusky通过对FPU问题的数学模型进行简化和运算发现FPU问题与KdV方程联系,并且他们对两个波速不同的孤波进行研究发现:孤波在碰撞前后保持高度不变,仅仅是波的轨迹发生偏离,于是他们引入了“孤立子”的概念来描述这种具有粒子性的孤波。
2. 非线性物理现象的发现和FPU问题的研究历史
2.1. 孤立子的发现
人们最初注意到非线性物理现象是在十八世纪三十年代。名为John Scott Russell的工程师在苏格兰联盟运河研究如何提高船舶的运输效率时,发现了一个保持形状的水团,该水团在一两英里之外的河道转弯处消失了。当时他对此现象十分震惊,Russell描述了他的发现过程 [1] :
I was observing the motion of a boat which was rapidly drawn along a narrow channel by a pair of horses, when the boat suddenly stopped—not so the mass of water in the channel which it had put in the channel which it had put in motion; it accumulated round the prow of the vessel in a state of violent agitation, then forward with great velocity, assuming the form of a large solitary elevation, a rounded, smooth and well-defined heap of water, which continued its course along the channel apparently without change of form or diminution of speed. I followed it on horseback, and overlook it still rolling on at a rate of some eight or nine miles an hour, preserving its original figure some thirty feet long and a foot to a foot and a half in height. Its height gradually diminished, and after a chase of one or two miles I lost it in the windings of the channel.
在观察到这个现象之后,Russell在实验室模拟了一系列实验,并在1844年发表了有关孤立波的文章并提出一种非线性的物理现象:具有较大振幅的孤立波比具有较小振幅的孤立波传播的更快。
2.2. KdV方程的提出
1895年荷兰物理学家Diederick Korteweg和他的学生Gustav de Vries提出了一个描述水波运动的非线性发展方程即KdV方程。他们导出了此微分方程的一个行波解来解释Russell所观察到的现象,同时他们也找到了周期性的解,但是并没有找到此非线性微分方程通解。
2.3. FPU问题的研究历史和孤立子的提出
1955年著名物理学家Fermi,计算机科学家Pasta和数学家Ulam提出了著名的FPU问题,并且他们借助第一台电子计算机MANIAC I进行数值实验,Mary Tsingou完成了其编程工作 [2] 。
Fermi,Pasta和Ulam用弹簧连接一串小球并给以一扰动,他们假定整个系统没有能量损失,并且振动仅沿着弹簧的方向,但是他们对弹簧的弹力添加了非线性部分,即 。一开始他们设想经过一定时间的振动,整个系统的能量会平均分配。当动力系统开始振动时,能量确实趋向于平均分配到不同的形式,各个能量态确实被激发,但是一天他们偶然间在动力系统达到稳定后继续运行程序,惊奇的发现大概97%的系统能量重新回到初始状态。
。一开始他们设想经过一定时间的振动,整个系统的能量会平均分配。当动力系统开始振动时,能量确实趋向于平均分配到不同的形式,各个能量态确实被激发,但是一天他们偶然间在动力系统达到稳定后继续运行程序,惊奇的发现大概97%的系统能量重新回到初始状态。
1965年,Zabusky和Kruskal开始从连续统一的角度考虑FPU问题。在连续的情况下,FPU问题可以近似用KdV方程来描述。并且他们对KdV方程中两个波速不同的孤波进行研究。发现如果这两个孤波开始分开并且波速大的在左边,那么在发生相互碰撞后,波速大的在右边并且保持最初的波形和速度,仅仅发生相位的移动。这两个孤波是弹性碰撞并且类似于粒子,因此被称为孤立子。
3. FPU问题中的耦合振子和简正模式
3.1. FPU问题的数学模型(图1)
FPU问题将其数学模型加入非线性部分,即 (
( 是小球的位移,
是小球的位移, 是常数,
是常数, 是非线性系数)。接下来再运用牛顿第二定律,我们可以得到描述第
是非线性系数)。接下来再运用牛顿第二定律,我们可以得到描述第 个振子的运动方程:
个振子的运动方程:
 ,
,
 ,
, 是第
是第 个小球的位移。整理上式右手边可得:
个小球的位移。整理上式右手边可得:
 ,
,
又可改写为:
 ,
,
 。
。
这是一个非线性二阶常微分方程组。为了理解这个方程组,接下来我们先考虑线性情况,即 的情况。
的情况。
3.2. 耦合振子和简正模式
现在我们将动力系统简化为三个弹簧联系两个质点如图2。
在这个动力系统里我们假设每个弹簧都遵守胡克定律,弹性系数为 ,质点的质量分别为
,质点的质量分别为 。我们假设在
。我们假设在 时刻动力系统在平衡状态被扰动,我们的目标是找到两个质点的位移函数
时刻动力系统在平衡状态被扰动,我们的目标是找到两个质点的位移函数 。
。
我们假定正方向为从左到右,两个墙壁之间的距离为L,弹簧的原始长度分别为 并假设动力系统在平衡状态下小球的位移分别为
并假设动力系统在平衡状态下小球的位移分别为 。
。
根据胡克定律我们可以知道第 个弹簧对第
个弹簧对第 个小球的力为:
个小球的力为:
 。
。
其中 是弹簧实际的长度,而
是弹簧实际的长度,而 是弹簧自然长度,并且我们设
是弹簧自然长度,并且我们设 。那么我们就会得到以下三个等式:
。那么我们就会得到以下三个等式:
 (1)
(1)
我们可以知道对 来说,它左边的弹簧给它
来说,它左边的弹簧给它 的力,它右边的弹簧给它
的力,它右边的弹簧给它 的力。由牛顿第二定律可得:
的力。由牛顿第二定律可得:
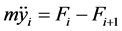
即:
 (2)
(2)
 (3)
(3)
将(1)代入可以得到:
 ,
,
 ,
,
将其写成矩阵形式:
 。 (4)
。 (4)
这是一个线性常微分方程组,如果我们定义一个线性算子 ,
, ,
, 其中
其中 是微分算子,并且
是微分算子,并且
 。
。
由常微分方程的理论可知线性方程的一个特点是方程组的通解总可以写成非齐次线性方程组的特解加上齐次线性方程组的通解。注意到(4)式的右边是一个常向量(不随时间变化),那么我们可以知道方程的非齐次特解一定是一个常向量:
 。
。
换句话说我们可以通过一个坐标变换将非齐次部分去掉:
 ,
,
其中 应该满足以下条件:
应该满足以下条件:
 。
。
所以我们可以得到 :
:
 ,
,
实际上这是整个动力系统的平衡点,在这一点(2) (3)式右边的力就消失了。
现在我们将注意力放在动力系统上,该动力系统在平衡位置处被扰动并且开始振动。我们可以将解决这个问题等价于解决以下的齐次方程:
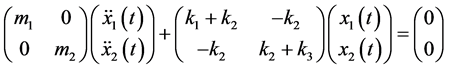
为了简化问题我们假设质量矩阵是单位矩阵,即 ,那么我们将会得到:
,那么我们将会得到:
 ,(5)
,(5)
或者我们可以写成:
 。
。
在这里 ,如果质量矩阵不是单位矩阵,那么
,如果质量矩阵不是单位矩阵,那么 将会和
将会和 不同。我们得到的这个形式是简谐运动的方程式。现在我们唯一的问题就是如何能让耦合振子转化为独立的两个振子也就是实现退耦,为了实现这一点我们就需要更换基底
不同。我们得到的这个形式是简谐运动的方程式。现在我们唯一的问题就是如何能让耦合振子转化为独立的两个振子也就是实现退耦,为了实现这一点我们就需要更换基底 。我们可以发现之所以我们的动力系统是耦合的,其原因是两个小球之间连接的弹簧。从矩阵中我们也可以看出这一点:
。我们可以发现之所以我们的动力系统是耦合的,其原因是两个小球之间连接的弹簧。从矩阵中我们也可以看出这一点: 仅出现在非对角位置,那么如果没有这个弹簧,我们的系统就会退化为两个分开的振子。所以对任意非零
仅出现在非对角位置,那么如果没有这个弹簧,我们的系统就会退化为两个分开的振子。所以对任意非零 ,行之有效的方法就是更换基底。
,行之有效的方法就是更换基底。
现在我们考虑(5)式,为了方便计算我们再做一假设: 。这样我们的动力系统就变成了左右对称的,但是注意这并不意味着动力系统的初始状态是否对称,其实我们对系统的扰动可以是任意的。
。这样我们的动力系统就变成了左右对称的,但是注意这并不意味着动力系统的初始状态是否对称,其实我们对系统的扰动可以是任意的。
在这样的假设下,我们动力系统方程就变为:
 。 (6)
。 (6)
在所有假设下,我们知道:
 。
。
那么我们的方程又可以写成以下的矩阵形式:
 , (7)
, (7)
然后我们将以下形式的试探函数代入(7)式:
 ,
,
得到:
 。
。
如果在任意时间 上式都要成立的话,我们就需要:
上式都要成立的话,我们就需要:
 。
。
其中 是单位矩阵。那么我们就可以发现:
是单位矩阵。那么我们就可以发现: 一定是矩阵
一定是矩阵 的特征向量,对应的特征根为
的特征向量,对应的特征根为 。而我们的特征根方程为:
。而我们的特征根方程为:
 ,
,
我们要想得到非零特征根就需要 。这样我们就会得到下面的等式:
。这样我们就会得到下面的等式:
 ,
,
解得:
 ,
,
对应的特征向量可以通过下面的方程求得:
 ,
,
对 我们有:
我们有:
 ,
,
所以我们就能得到:
 。
。
对 我们有:
我们有:
 ,
,
我们可以得到:
 ,
,
那么(6)式的通解就是:
 。
。
在这里我们有四个参数 ,这四个参数可以通过初始条件确定下来。因为我们有两个质点,初始状态会给出每一个质点在
,这四个参数可以通过初始条件确定下来。因为我们有两个质点,初始状态会给出每一个质点在 时的位置和速度,那么我们就可以通过四个方程算出这四个参数。
时的位置和速度,那么我们就可以通过四个方程算出这四个参数。
下面我们从物理角度来解释这个动力系统:
1) 对于第一种模式,即 ,两个小球的运动是相同的,即
,两个小球的运动是相同的,即 。这就意味着两个小球之间的弹簧一直保持着一定的长度没有变化,它对振动的频率也没有任何影响。
。这就意味着两个小球之间的弹簧一直保持着一定的长度没有变化,它对振动的频率也没有任何影响。
2) 对于第二种模式,即 ,两个小球的运动是对应相反的,即
,两个小球的运动是对应相反的,即 。这就意味着两球之间的弹簧的伸缩量是两边弹簧的二倍。
。这就意味着两球之间的弹簧的伸缩量是两边弹簧的二倍。
我们的分析结果表明这个系统的任意振动形式都可以用以上两种运动模式的线性组合来表示。
3.3. 简正模式和能量守恒
在上一部分我们已经看到了简正模式 可以帮助我们找到方程(6)的解。下面这一部分我们将会考虑更加一般的对角化过程以及解决具有
可以帮助我们找到方程(6)的解。下面这一部分我们将会考虑更加一般的对角化过程以及解决具有
 , (8)
, (8)
形式的齐次线性方程微分方程的过程。
如果 是可对角化的,也即,如果存在矩阵
是可对角化的,也即,如果存在矩阵 使得
使得
 ,(9)
,(9)
其中 是对角阵,
是对角阵,
 ,
,
那么我们可以按以下的步骤来解决(8)式:我们在(8)式左边乘上 然后再在算子的右边插入一个单位矩阵
然后再在算子的右边插入一个单位矩阵 ,得到:
,得到:
 ,
,
这个式子又可以写成:
 。
。
将(9)式代入得:
 ,
,
在这里我们定义简正坐标:
 。
。
在这个基底下我们的方程是可对角化的因为包含 的那个方程不会包含其他的未知量。并且每个
的那个方程不会包含其他的未知量。并且每个 都对应一个唯一的特征频率
都对应一个唯一的特征频率 ,这里的
,这里的 则对应于对角矩阵
则对应于对角矩阵 对角线上的第
对角线上的第 个元素的平方根。
个元素的平方根。
在新的基底 下方程是退耦的,每个等式都表示一个简谐振子的运动:
下方程是退耦的,每个等式都表示一个简谐振子的运动:
 。 (10)
。 (10)
根据前一部分的论述,我们知道(10)式的解的形式是:
 ,
,
其中 将会通过初始条件确定下来。而
将会通过初始条件确定下来。而 是原坐标
是原坐标 的线性组合。那么我们可以得到:
的线性组合。那么我们可以得到:
 。
。
用向量形式表示则是:
 ,
,
其中
 ,
,
是 的第
的第 个特征向量,其对应的特征值为
个特征向量,其对应的特征值为 。
。
其实矩阵 由
由 的特征向量
的特征向量 组成,(9)式又等价于说:对任意
组成,(9)式又等价于说:对任意 ,特征向量
,特征向量 和特征值
和特征值 将会解决特征值问题:
将会解决特征值问题:
 。
。
在二维系统里我们对特征值问题有两个解,也即两个简正模式。那么(8)式的解就是以上两个解的线性组合:
 。
。
相似的,在一个自由度为 的系统里,我们将会有
的系统里,我们将会有 个这样的模式,而方程的通解将是这
个这样的模式,而方程的通解将是这 个解的线性组合。
个解的线性组合。
从我们之前的分析我们知道了三个弹簧对两个小球的力分别是:

现在我们现在从能量的角度来分析这个系统,三个弹簧的势能为:
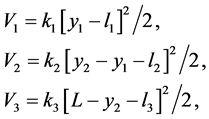
那么整个系统的势能为:
 。
。
我们可以通过对势能求导展开得到在第 个小球的合力,即
个小球的合力,即 。如果我们在平衡点用这个方法求合力的话,那么我们一定得到:
。如果我们在平衡点用这个方法求合力的话,那么我们一定得到: 。因为势能实际上是一个二次型,它的展开可以分为两部分,一部分是系统在关于平衡位置伸长的势能,也是一个二次型;另一部分则是一个常数,也即应用等式
。因为势能实际上是一个二次型,它的展开可以分为两部分,一部分是系统在关于平衡位置伸长的势能,也是一个二次型;另一部分则是一个常数,也即应用等式 (其中
(其中 是固定的,并且
是固定的,并且 使得
使得 )我们可以得到:
)我们可以得到:
 ,
,
其中
 。
。
现在我们考虑系统的动能:
 ,
,
系统的总能量为:
 ,
,
方程用矩阵写出来就是:
 ,(11)
,(11)
其中
 ,
, ,
,
接下来我们求 对
对 求导数我们可以得到:
求导数我们可以得到:
 ,
,
这样我们就可以直观的看到:加号两边的两个部分都分别为零,因为我们知道 和
和 。
。
现在我们来考虑(11)式,我们对该式重新定标,令 。然后我们就会得到以下的表达式:
。然后我们就会得到以下的表达式:
 ,
,
在这里
 ,
,
 ,
,
我们可以知道在这里 是依然是对称矩阵。
是依然是对称矩阵。
从上式我们发现动能部分有一个单位矩阵,所以我们的问题就是势能部分。那么我们的下一步就是去对角化矩阵 。而我们知道对称矩阵总是可对角化的,在这里我们用正交阵来使
。而我们知道对称矩阵总是可对角化的,在这里我们用正交阵来使 对角化:
对角化:
 ,
,
类似于我们开始讨论简正坐标,系统的运动方程有以下的对角形式:
 ,
,
并且在这里 ,或者说
,或者说 。用这个基底来表达能量式我们会得到:
。用这个基底来表达能量式我们会得到:
 。
。
那么我们最后的表达式就是对角的。更加具体地说,我们用简正坐标的时候我们的势能表达式为:
 ,
,
再考虑到系统的动能为 ,那么每一个简正模式在贡献能量方面都是独立的:
,那么每一个简正模式在贡献能量方面都是独立的:
 ,
,
 。
。
而实际上在每个简正模式下,能量都是守恒的:
 。
。
这也是简正模式十分重要的一个特点。
4. 从FPU问题到孤立子
4.1. 从FPU问题到KdV方程
在讨论FPU问题的数学模型时,我们得到了下式 [3] :
 , (12)
, (12)
其中
 。
。
现在我们来考虑真正的FPU问题,即包含非线性部分的FPU问题。
1965年Kruskal和Zabusky研究了有关FPU问题的连续极限问题。他们用一个关于时间和位置的连续函数逼近 ,并且在
,并且在 这一点对函数进行泰勒展开:
这一点对函数进行泰勒展开:
 ,
,
其中 。我们令
。我们令 ,然后可以得到:
,然后可以得到:
 。
。
然后再将泰勒展式代入(12)式,那么就会得到连续方程:
 ,
,
也即:
 ,(13)
,(13)
其中 ,并且我们忽略次数高的项。这个等式是由Boussinesq得到的。在这里我们对此等式有以下四个讨论:
,并且我们忽略次数高的项。这个等式是由Boussinesq得到的。在这里我们对此等式有以下四个讨论:
1) 当 并且
并且 时,我们就可以忽略
时,我们就可以忽略 和
和 。那么(13)式就可以看成以下的线性波动方程:
。那么(13)式就可以看成以下的线性波动方程:
 。
。
2) 当 ,那么我们可以忽略
,那么我们可以忽略 项。(13)式就变成了以下线性波动方程:
项。(13)式就变成了以下线性波动方程:
 。
。
3) 当 ,那么我们可以忽略
,那么我们可以忽略 。(13)式就变成了:
。(13)式就变成了:
 。
。
4) 当 ,这时候将出现“最大平衡”的情形,这也是最有意思的一个情形,我们将在下面详细讨论。接下来我们尝试找具有以下形式的
,这时候将出现“最大平衡”的情形,这也是最有意思的一个情形,我们将在下面详细讨论。接下来我们尝试找具有以下形式的 作为方程的解:
作为方程的解:
 ,
,
这里我们有:
 ,
,
 ,
,
 ,
,
将得到的这三个式子代入连续极限(13)式得到:
 。
。
下面我们令 并且忽略掉
并且忽略掉 ,那么我们就会得到:
,那么我们就会得到:
 ,(14)
,(14)
其中 并且
并且 是初始条件。式(14)其实就是著名的Korteweg-de Vries (KdV)方程。Boussinesq得出来(13)和(14)式,后来Korteweg和de Vries找到了这个方程的椭圆余弦波解。在19世纪60年代之前,KdV方程最主要的用来研究水波,而且当时许多数学家对KdV方程并不感兴趣,他们的精力集中于线性方程上。
是初始条件。式(14)其实就是著名的Korteweg-de Vries (KdV)方程。Boussinesq得出来(13)和(14)式,后来Korteweg和de Vries找到了这个方程的椭圆余弦波解。在19世纪60年代之前,KdV方程最主要的用来研究水波,而且当时许多数学家对KdV方程并不感兴趣,他们的精力集中于线性方程上。
所以我们通过对FPU问题进行线性极限的讨论,得到了熟知的KdV方程。
4.2. 从KdV方程到孤立子
在上面的讨论中我们得到了KdV方程即(14)式,不失一般性我们可以考虑下列方程:
 。
。
我们考虑具有 形式的行波解,其中
形式的行波解,其中 ,
, 为常数。那么我们的方程就变成了:
为常数。那么我们的方程就变成了:
 ,
,
对方程两边同时积分可以得到:
 ,
,
在上式两边同时乘上 再积分可得:
再积分可得:
 ,
,
为了得到孤立波解我们要求当 时,
时, ,同时我们取
,同时我们取 ,那么就有
,那么就有
 ,
,
从而:
 ,
,
下面我们令 ,那么上式将变成:
,那么上式将变成:
 ,
,
可解得
 ,
,
再由 可得:
可得:
 。
。
这样我们就得到了孤波解。现在我们画出 时刻的图像(图3)。
时刻的图像(图3)。
通过图像我们可以看到随着时间的推移我们的波形并没有变化,孤波仅仅发生了位置的改变,这也就是我们所说的孤立子。我们还可以观察两个孤立波解的情况,给出解的表达式为 [4] :
 ,
,
其中 ,下面我们取
,下面我们取 ,
, ,
, 画出图4,其中横坐标为时间纵坐标为位置,在图中我们可以看出两列孤波在
画出图4,其中横坐标为时间纵坐标为位置,在图中我们可以看出两列孤波在 和
和 之间相遇,而在相遇前后两列波的颜色与相遇之前比较是没有区别的,仅仅是两个波的传播方向发生了一个小的位移,这就表明两列孤波相遇之后,波形保持不变,这是孤波的一个重要特点。
之间相遇,而在相遇前后两列波的颜色与相遇之前比较是没有区别的,仅仅是两个波的传播方向发生了一个小的位移,这就表明两列孤波相遇之后,波形保持不变,这是孤波的一个重要特点。
致谢
至此感谢刘青平教授以及李再兴副教授对此文章的指导。