1. 引言
为了解决网络的带宽难以承载巨大的图像数据传输速率,人们利用图像压缩技术在图像数据处理、传输和存储前进行必要的压缩,并使压缩后的数字图像信息以不同的形式在网络上方便地传输、交流。与此同时,数字图像信息的安全与保密显得尤为重要。如果直接对图像信息进行加密,必然不能再进行图像压缩,从而很难减少用于传输和存储的工作量。由于需要压缩的图像(如JPEG图像)或多媒体数据,其数据压缩算法一般是在频域进行的,如果将压缩算法与频域加密算法结合进行,就不会增加太多的计算量。对于图像频域的加密算法,以运算速度快,加密强度(置乱度)高,抗干扰能力强,工程应用软、硬件实现简单为追求目标。但是,运算速度快、加密强度高、实现简单是相互制约3个因素,不可能同时实现,只能在一定的条件下,提出合适的加密方案。
近年来,混沌密码学作为一种新的加密技术应运而起,并成为现代密码学的重要研究内容。混沌序列[1] 主要表现为对初始值和系统参数的极端敏感性、白噪声的统计特性和混沌序列的遍历特性,具有不可预测性以及混沌序列的快速生成性。目前,在DCT变换域实现压缩图像加密的文献并不多,但大都存在由于加密操作,而降低了图像压缩比的问题,这也是实际工程应用中不希望发生的。所以本文从JPEG图像压缩标准的特征出发,结合混沌动力学的突出特点,提出了一种图像DCT域的混沌加密方法,这种方式既能保证压缩比,又能实现图像信息的安全保密。
2. 算法实现
2.1. JPEG图像压缩算法特征分析
JPEG算法[2] -[4] 框图如图1所示,假设原始图像大小为M*N。压缩时,将原始图像数据分成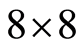 数据单元矩阵。
数据单元矩阵。
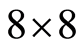 的图象经过DCT变换后,其低频分量都集中在左上角,高频分量分布在右下角,其中F(0, 0)(即第一行第一列元素)代表了直流(DC)系数,即
的图象经过DCT变换后,其低频分量都集中在左上角,高频分量分布在右下角,其中F(0, 0)(即第一行第一列元素)代表了直流(DC)系数,即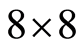 子块的平均值,要对它单独编码。
子块的平均值,要对它单独编码。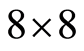 的其它63个元素是交流(AC)系数,采用行程编码,其需要按照“之”字型(Zig-Zag)的方式排列(如图2所示),以增加行
的其它63个元素是交流(AC)系数,采用行程编码,其需要按照“之”字型(Zig-Zag)的方式排列(如图2所示),以增加行

Figure 1. JPEG agrithm frame
图1. JPEG算法框图

Figure 2. Zig-Zag rank
图2. Zig-Zag排序
程中连续“0”的个数。由于低频分量包含了图象的主要信息,而高频与之相比,就不那么重要了,所以通过量化操作去掉高频分量,保持低频分量。这样,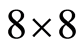 的图像DCT系数矩阵中,只有左上角含有些许的非零元素值,而右下角大部分都是零值元素,这也使得前面提到的行程编码更为有效。
的图像DCT系数矩阵中,只有左上角含有些许的非零元素值,而右下角大部分都是零值元素,这也使得前面提到的行程编码更为有效。
加密算法应发生在DCT系数量化之后。如果利用混沌序列产生的位置置乱矩阵直接加密量化后的DCT系数矩阵(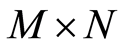 ),必然会破坏DCT系数的概率分布函数,从而使后续的编码无法按照最优的方式操作,使压缩效率降低。因此在文献5的基础上,把空域中以块为单元的置乱技术应用到频域中。按照JPEG算法分块原则,将DCT系数矩阵分成
),必然会破坏DCT系数的概率分布函数,从而使后续的编码无法按照最优的方式操作,使压缩效率降低。因此在文献5的基础上,把空域中以块为单元的置乱技术应用到频域中。按照JPEG算法分块原则,将DCT系数矩阵分成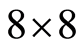 子块,使得在置乱的过程中保持了每个
子块,使得在置乱的过程中保持了每个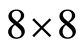 的图像DCT系数矩阵的特征,不至于影响整幅图像的压缩效率。块置乱过程可如图3所示。
的图像DCT系数矩阵的特征,不至于影响整幅图像的压缩效率。块置乱过程可如图3所示。
为了提高系统的安全性,还需要对置乱后的DCT系数矩阵中的系数值进行变换。[5] 中提出了用混沌矩阵与DCT系数矩阵中的每一元素的绝对值进行异或操作。这种方式存在一定的不足,只有DCT系数矩阵中连“0”数越多,压缩效率才会越高,并且在每个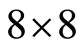 的图像DCT系数矩阵中“0”的数目占有率很高,如果利用混沌序列与“0”值进行异或,势必会大大增加DCT系数矩阵非零元素个数,而降低零元素个数,从而影响压缩率。因此,本文采用只对感兴趣DCT系数(绝对值)进行异或的加密方式,并且若加密后DCT系数值变为“0”,则再次异或,也就是不加密此DCT系数。原因在于:在频域中每一点的变化对整个数据集合都会产生一定的影响,图像数据经过DCT变换得到的DCT系数中,如果有一个发生改变,就会通过IDCT逆运算体现在所有的象素点中。每个DCT系数由两部分组成,DCT系数绝对值以及系数的符号位,可见,任何一个不正确的话,都很难恢复原图像。若某个DCT系数的绝对值与混沌值异或后变成“0”值系数,由于“0”是一个没有符号的数,则在解密过程中,很难确定异或前此系数的符号位。所以不适合对其进行加密。
的图像DCT系数矩阵中“0”的数目占有率很高,如果利用混沌序列与“0”值进行异或,势必会大大增加DCT系数矩阵非零元素个数,而降低零元素个数,从而影响压缩率。因此,本文采用只对感兴趣DCT系数(绝对值)进行异或的加密方式,并且若加密后DCT系数值变为“0”,则再次异或,也就是不加密此DCT系数。原因在于:在频域中每一点的变化对整个数据集合都会产生一定的影响,图像数据经过DCT变换得到的DCT系数中,如果有一个发生改变,就会通过IDCT逆运算体现在所有的象素点中。每个DCT系数由两部分组成,DCT系数绝对值以及系数的符号位,可见,任何一个不正确的话,都很难恢复原图像。若某个DCT系数的绝对值与混沌值异或后变成“0”值系数,由于“0”是一个没有符号的数,则在解密过程中,很难确定异或前此系数的符号位。所以不适合对其进行加密。
2.2. 混沌加密算法设计
2.2.1. 置乱矩阵与变换矩阵的生成
Logistic映射[6] 是一个典型非线性混沌方程,它起源于一个人口统计的动力学系统,虽然简单却体现
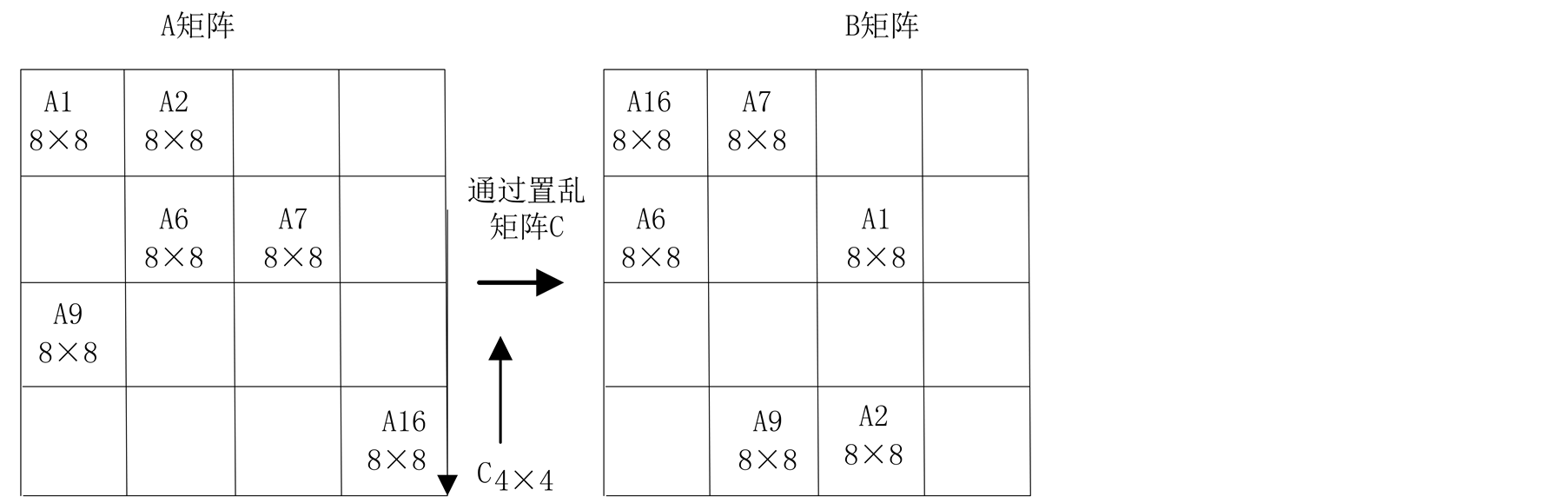
Figure 3. Curve: system result of standard experiment
图3. 图像块置乱
出混沌运动的基本特性。Logistic映射如下式:
 (1)
(1)
式中,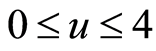 ,
,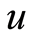 为控制参数,
为控制参数,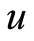 确定后,由任意初值
确定后,由任意初值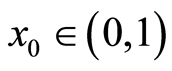 ,可迭代出一个确定的序列
,可迭代出一个确定的序列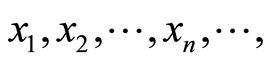 对于不同的
对于不同的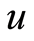 值,系统式将呈现不同的特性。当
值,系统式将呈现不同的特性。当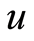 达到极值
达到极值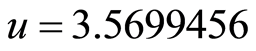 时,系统的稳态解为周期2
时,系统的稳态解为周期2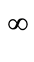 ,此时系统进入混沌状态。
,此时系统进入混沌状态。
利用(1)式迭代产生混沌序列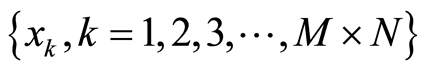 ,提取
,提取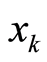 的前
的前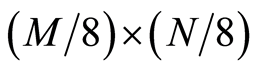 项,以行为主序,依次排列成
项,以行为主序,依次排列成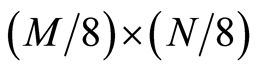 位矩阵J。对J中的元素按由大到小的原则进行排序,并按行优先的方式生成矩阵G,则由G中的每个元素在原矩阵J中的位置坐标形成置乱矩阵
位矩阵J。对J中的元素按由大到小的原则进行排序,并按行优先的方式生成矩阵G,则由G中的每个元素在原矩阵J中的位置坐标形成置乱矩阵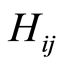 (
(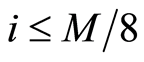 ,
,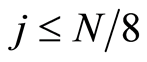 )。再将序列
)。再将序列 中的每一个元素进行放大,量化和模运算double(mod(round(
中的每一个元素进行放大,量化和模运算double(mod(round(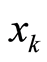 -*10^14), 256) + 1)并按行优先的方式生成变换矩阵
-*10^14), 256) + 1)并按行优先的方式生成变换矩阵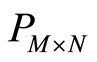 。
。
2.2.2. 符号矩阵的生成
在符号矩阵的生成过程中,需要用到另一个混沌模型。方程如下:
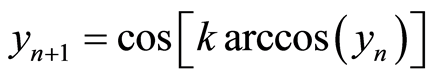 (2)
(2)
其定义区间为(‒1, 1),当参数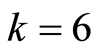 时,Chebychev系统[7] 的Lyapunov指数为1.791733…,映射工作于混沌状态。利用(2)式迭代产生序列
时,Chebychev系统[7] 的Lyapunov指数为1.791733…,映射工作于混沌状态。利用(2)式迭代产生序列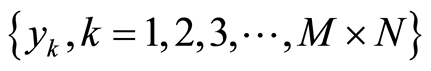 ,通过比较序列
,通过比较序列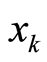 与
与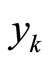 的大小,生成符号变换序列,在按照行优先的方式生成符号矩阵S。文中没有将Chebychev的初始值
的大小,生成符号变换序列,在按照行优先的方式生成符号矩阵S。文中没有将Chebychev的初始值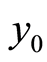 以及参数
以及参数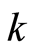 作为加密系统的密钥,而是由
作为加密系统的密钥,而是由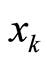 中的某两个值经过线性变换获得。假设解密时仅仅是参数
中的某两个值经过线性变换获得。假设解密时仅仅是参数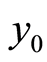 或者
或者 不正确,其它密钥都正确,解密后的图像中会体现原始图像的大部分信息。原因是量化后DCT系数矩阵中,零元素的比例高,符号矩阵只相当于对极个别的非零元素加密,也就是说单纯地利用符号矩阵进行加密并不能很好扰乱图像信息,必要产生错误参数解密后的图像隐含原图像的大部分信息,使得破译者很容易破译。所以,此时
不正确,其它密钥都正确,解密后的图像中会体现原始图像的大部分信息。原因是量化后DCT系数矩阵中,零元素的比例高,符号矩阵只相当于对极个别的非零元素加密,也就是说单纯地利用符号矩阵进行加密并不能很好扰乱图像信息,必要产生错误参数解密后的图像隐含原图像的大部分信息,使得破译者很容易破译。所以,此时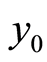 以及参数
以及参数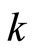 属于非常弱密钥,不适合作为系统的关键密钥。由下面的方程得到符号矩阵。
属于非常弱密钥,不适合作为系统的关键密钥。由下面的方程得到符号矩阵。
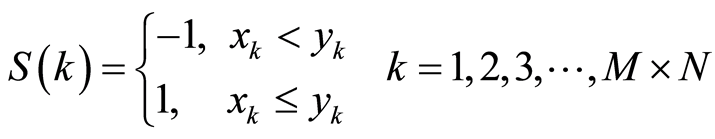 (3)
(3)
2.3. 加密算法实现
本文将Logistic映射的初始参数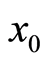 以及控制参数
以及控制参数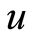 作为系统的初始密钥。
作为系统的初始密钥。
具体的加密过程如下:假设待加密图像I大小为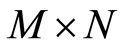 ,灰度级别为0-255。
,灰度级别为0-255。
步骤1:由Logistic映射在密钥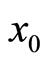 ,
,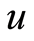 的作用下生成实数值混沌序列
的作用下生成实数值混沌序列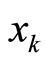 ,Chebychev映射在密钥
,Chebychev映射在密钥 ,
,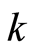 的作用下生成混沌序列
的作用下生成混沌序列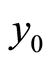 。
。
步骤2:由混沌序列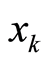 按照1.2.1节所述,生成位置置乱矩阵H和变换矩阵P。再按照1.2.2所述,由
按照1.2.1节所述,生成位置置乱矩阵H和变换矩阵P。再按照1.2.2所述,由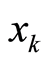 与
与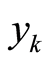 生成符号变换矩阵
生成符号变换矩阵
步骤3:将图像I进行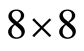 DCT变换,用量化表对其进行量化。
DCT变换,用量化表对其进行量化。
步骤4:将DCT系数矩阵按JPEG中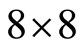 的标准分块,并按行序对块进行编号,利用置乱矩阵H置乱DCT系数矩阵。
的标准分块,并按行序对块进行编号,利用置乱矩阵H置乱DCT系数矩阵。
步骤5:用P对置乱的DCT系数矩阵中的每一个元素的绝对值进行异或,异或中采取感兴趣系数(图像的低频成分)加密方式,并针对异或后DCT系数值变为“0”的元素,利用两次异或的原则维持原系数值。
步骤6:利用符号矩阵S点乘DCT系数矩阵。
步骤7:保存为JPEG图像。
解密算法是加密算法的对称逆过程,在解密过程中要先点乘符号矩阵,再进行异或运算和位置置乱。输入正确密钥后,就可以解密出原DCT系数矩阵,通过IDCT恢复出原始图像。
3. 仿真实验与分析
下面是以cameraman (256*256)图像为例,利用Matlab进行的实验仿真。由于JPEG图像压缩中的量化并不是本文讨论的重点,所以本文只是利用图4所示的二值掩模来量化每个8 × 8的图像DCT系数矩阵,这里保留DCT变换的15个系数。
 (4)
(4)
系统加密过程中选择的密钥分别为 ,
,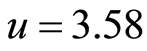 ,
,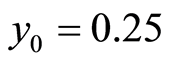 ,
,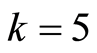 。鉴于DCT转换公式所接受的数字范围是在−128到+127之间[8] ,需要将cameraman图像中的每个像素减去128方可进行DCT变换。文中通过下述代码完成图像DCT变换及量化过程。
。鉴于DCT转换公式所接受的数字范围是在−128到+127之间[8] ,需要将cameraman图像中的每个像素减去128方可进行DCT变换。文中通过下述代码完成图像DCT变换及量化过程。
1) I = imread('cameraman.tif'); I = im2double(I);
2) I1 = 255*I -128; T = dctmtx(8);
3) B = blkproc(I1,[8 8],'P1*x*P2',T,T');
4) B1 = blkproc(B,[8 8],'P1.*x',mask);
5) B2 = round (0.5*B1);
其中,B为得到的图像DCT系数矩阵,B2为量化后的系数矩阵。具体的仿真结果如图4所示:(a)和(b)是原明文图像和原DCT系数,(c)和(d)加密后的DCT系数以及加密后的图像。(e)和(f)正确参数解密出来的图像和错误参数解密出来的图像,(g)和(h)原始图像的直方图和加密后图像的直方图。
从上面的仿真结果可以看出,原始图像的象素在各种灰度级上的分布是不均匀的,但经过混沌系统加密后,破坏了原有图像的统计规律,有较好的密文扩散性。只要输入正确的密钥,就能很好地将压缩
后的图像解密出来,解密出的压缩图像与原图像基本一致,看不出差异;当解密密钥与加密密钥存在细微差别时,也不能正确地解密出原始图像。
密文对密钥的敏感性是指对同一明文图像,采用两个略有差异的密钥分别进行加密后得到的密文图像的差别。两次加密时仅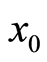 不同
不同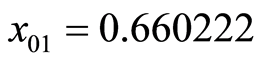 ,
,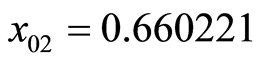 ,然后将得到的两个加密压缩图像进行对比。图5是取两个密图前256个密文像素的差值绘制出来的分布图。由图结果可知,相同的明文在密钥发生细微变化时,密文会有显著变化,这反映了密文对密钥的敏感性。多次实验表明,任何密钥细小的改变都会使密文发生显著的变化。
,然后将得到的两个加密压缩图像进行对比。图5是取两个密图前256个密文像素的差值绘制出来的分布图。由图结果可知,相同的明文在密钥发生细微变化时,密文会有显著变化,这反映了密文对密钥的敏感性。多次实验表明,任何密钥细小的改变都会使密文发生显著的变化。
算法安全性分析中还包括图像相邻象素的相关性分析,加密的目的之一就是降低图像相邻象素的相关性。由于JPEG压缩属于有损压缩,由极少数的量化系数值经过IDCT恢复原图像,所以频域中加密系统对象素相关性的影响效果不如空域好,但是如前所述空间域的局部随机置乱效果不如频域好。本文分别从原始图像以及压缩加密图像上随机的选择16384对相邻像素。然后利用下面的两个公式计算他们的相关系数[9] :
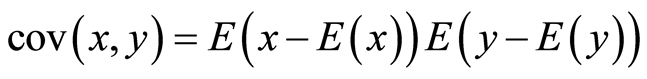 (5)
(5)
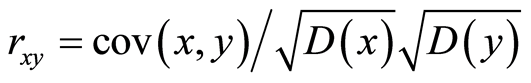 (6)
(6)
其中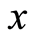 和
和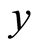 是对应于图像中两个相邻像素的灰度值。在数值计算中,使用下列离散公式:
是对应于图像中两个相邻像素的灰度值。在数值计算中,使用下列离散公式:
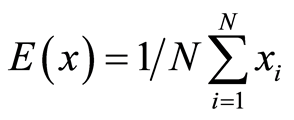 (7)
(7)
 (8)
(8)
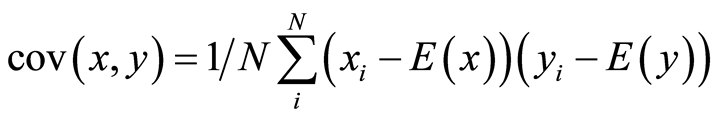 (9)
(9)
表1还计算了3种方向上的相关系数。可以看出原图像的相邻象素的相关系数集中在0.95附近,而加密后图像的相关系数在0.5附近,达到了降低相关性的目的。
压缩图像数据在传输过程中难免会遇到各种噪声,所以好的算法应该有很强的抗噪声能力。图6(a)是对密文图像加入10%的椒盐噪声[10] 后所得到的密文,对它解密得到图6(b)。图6(c)是对密文图像加入20%的高斯噪声[10] 后所得到的密文,对它解密得到图6(d)。通过解密后的效果,应能看出原图的大致模样。可见该算法有很好的抗噪声能力。
除了上述分析外,还将本文的算法运行时间和压缩效率与文献[11] 及[12] 进行了比较。并且本文算法的时间开销中,也包含了混沌密钥的生成时间。由表2可见,本算法的时间开销很小,具有很快的加密速度。
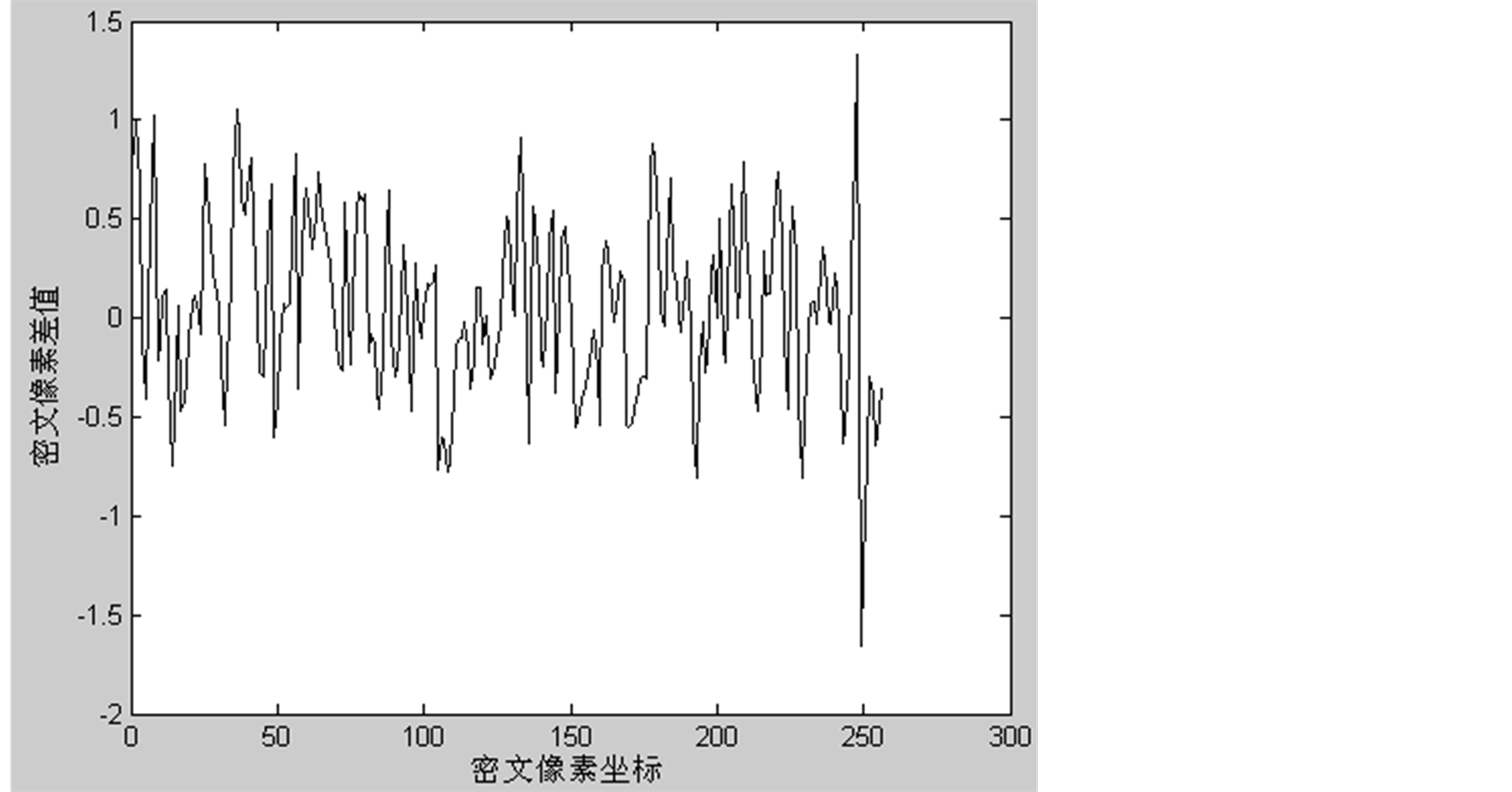
Figure 5. Pixel value difference distributing of two Ciphertexts
图5. 两幅密文像素差值分布图
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 6. Decryption result of cryptograph with noise. (a) cryptograph with pepper noise, (b) Encryption of (a), (c) cryptograph with guassian noise, (d) Encryption of (c)
图6. 对密文加入噪声后的解密结果。(a) 加入椒盐噪声的密文,(b) 对于(a)解密出来的图像,(c) 加入高斯噪声的密文,(d) 对于(c)解密出来的图像

Table 1. The correction coefficients of plaintext image and cryptograph image
表1. 明文和密文相邻像素的相关系数

Table 2. Compare of operation and compression ratio
表2. 运算与压缩效率比较
4. 结束语
本文就JPEG图像压缩的特点,提出了一种图像DCT域的混沌加密方法。针对图像DCT系数矩阵经量化后的特性,在利用空域中以象素块为单位的置乱基础上,提出只对感兴趣系数加密以及异或后为“0”值的元素再次异或的方案,以此来保证了图像的高压缩率。通过实验仿真和性能分析,验证了本算法简单,速度快,加密效果好等特点。
资助信息
总装备部基金资助项目(KYC-XZ-XM-2010-32)。