1. 引言
在大学物理专业的理论力学、电磁学、电动力学和场论等课程中，经常采用矢量微分算符∇来表示可微函数的梯度、散度、旋度等，如gradw = ∇w，div A ⃗= ∇∙A ⃗，rot A ⃗ = ∇ × A ⃗，其中w为三维空间的一个标量场，A ⃗为三维空间中的一个矢量场 [1] - [4] 。标量场的梯度、矢量场的散度和旋度是物理场本身的内禀性质，不依赖于坐标系的选择；但在不同的坐标系中其计算形式却十分不同，表达式非常复杂，因而经常容易出错。对此，以前的文献中也有很多研究和讨论，但其中绝大部分是通过坐标变换来阐释和说明的 [5] - [8] 。针对一般正交曲线坐标系的情况，根据坐标变换人们给出了采用拉梅系数等成熟的方法，但要理解物理场梯度、散度、旋度计算的内涵还是需要用几何的方法进一步的研究、解析和澄清。
本文将利用黎曼几何和张量分析的知识和概念 [9] - [12] ，推导在一般曲线坐标系中梯度、散度、旋度的计算公式，以帮助人们理解和认识拉梅系数的产生根源。由于在三维平直空间中采用笛卡尔坐标系(直角坐标系)，其中的矢量的逆变和协变对应分量刚好相同，因此我们在直角坐标系中讨论问题时就不必区分它们。但是，即使在三维平直空间中，只要不采用直角坐标系，那么问题就会变得比较复杂，我们必须区分矢量的逆变和协变，也必须搞清楚正交曲线坐标系的基底和对应的活动标架的基底的区别和联系。事实上，通常的教科书中给出的正交曲线坐标系中的表达式，都是针对局域活动标架的结果，与黎曼几何中的坐标基底(逆变矢量)、对偶基底(协变矢量)还相差着一个变换关系。
2. 梯度、散度、旋度的坐标表述和几何表述
2.1. 标量场的梯度和矢量场的散度、旋度在不同坐标系下的计算公式
物理场是空间和时间的函数，如标量场
、矢量场
，当它们与时间无关时则称为稳定场。本文只讨论物理场的空间变化性质，当然只涉及对空间坐标的偏微分。在直角坐标系中，标量场的梯度和矢量场的散度、旋度可以直接利用直角坐标系中的矢量微分算子(哈密顿算子)
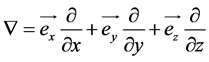进行计算。此时，标量场
的梯度：
。
矢量场
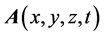的散度：
。
矢量场
的旋度：
。
标量场
的拉普拉斯算子：
。
然而，在三维空间的柱坐标系和球坐标系之下矢量微分算子(哈密顿算子)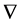
的定义分别为
和
。此时我们无法直接利用直角坐标系中类
似的简单计算得到梯度、散度和旋度，而是必须考虑和利用拉梅系数，一般性的公式如下：
， (1)
(2)
(3)
(4)
其中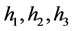
为拉梅系数，
为相应的坐标。对直角坐标系，有
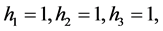
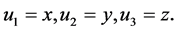
对柱坐标系，有
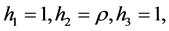
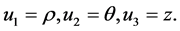
对球坐标系，有
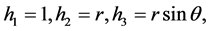
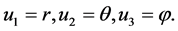
2.2. 黎曼几何中标量场的梯度、矢量场的散度和旋度的定义
在黎曼几何中，三维空间中的线元为不变量，其表达式为：
(5)
其中
为在某一坐标系之下表示空间几何的度规张量(协变张量)。对应的行列式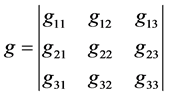
称为度规行列式，而对应的
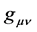的逆矩阵
则是表示空间几何的逆变度规张量(逆变张量)。
根据黎曼几何和张量分析的基本理论，标量场的梯度、矢量场的散度和旋度都是不依赖于坐标系的；而且由于度规的存在，所有的空间张量场(当然包括矢量场)都可以通过协变度规和逆变度规把相应的指标降下来或升上去。在这样的几何背景之下，一个标量场
的梯度为协变矢量，其定义为：
。 (6)
矢量场
的散度为标量，定义为：
。 (7)
矢量场的旋度公式比较复杂，利用黎曼几何理解旋度公式需要先用到体元的概念。体元是指一个 阶的全反称张量场，它需要满足连续且处处非零2个条件。一般而言，体元的选择具有相当的任意性；但当指定一个度规之后，可以选择体元满足下述条件：
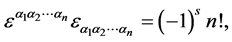
其中s代表线元表达式中系数为-1的坐标个数。这种体元叫做与度规适配的体元，一般指定度规后，体元默认采用与度规适配的体元。
有了体元的概念之后，三维空间中一个矢量场的旋度可以表示为
(8)
在上述公式中，矢量场
取其协变矢量的形式，而其旋度
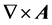则为逆变矢量的形式。由于体元具有全反称性质，如涉及坐标系下的分量，则体元的三个指标必须不同。对于正定度规，体元在某一坐标系下的分量满足如下数值：
(9)
为度规行列式。容易看出，
。
标量场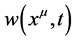
的拉普拉斯算子为标量，其定义为：
。 (10)
3. 正交曲线坐标系下梯度、散度和旋度的一般计算方法
3.1. 坐标系的基底和局域活动标架的基底之间的关系
直角坐标系和柱坐标系之间的变换关系为：
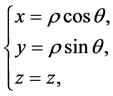
取微分，有
，
这是2组对偶矢量之间的变换关系，左边是直角坐标系的对偶坐标基底，但是右边并不是柱坐标系的对偶坐标基底，而是局域活动标架的对偶基底，这样可以保证它们的正交归一性。
根据对偶矢量的定义，对偶基底之间的变换关系就是矢量的分量之间的变换关系，而矢量分量之间的变换关系和基底之间的变换关系是互逆的，因此有
，
这样，通常的直角坐标系的基底与柱坐标系的基底的变换关系为
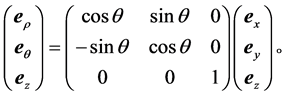
我们通常教科书中使用的柱坐标系的基底，并不是柱坐标系的黎曼几何意义下的坐标基底，而是经过了单位化处理之后的基底，满足正交归一条件，本文中称这套基底为局域活动标架的基底。另外，满足正交归一条件的局域活动标架基底，其逆变形式与协变形式相同，这点类似于我们的直角坐标系，可以把局域活动标架看作是局域的小直角坐标系。
对任意的一个逆变矢量
，在柱坐标系之下，可以利用局域活动标架基底和坐标系的基底，有两种展开形式，即
，
。 (11)
类似地，对任意的一个协变矢量
，在柱坐标系之下，可以利用局域活动标架基底和坐标系的对偶基底，有两种展开形式，即
，
。
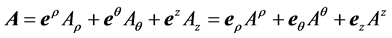同样，直角坐标系和球坐标系之间的变换关系为：
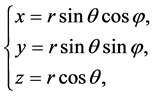
取微分，有
，
这是2组对偶矢量之间的变换关系，左边是直角坐标系的对偶坐标基底，但是右边并不是球坐标系的对偶坐标基底，而是局域活动标架的对偶基底，这样可以保证它们的正交归一性。
计算上式中变换矩阵的逆矩阵，得直角坐标系与通常所述的球坐标系的基底之间的变换关系为：
，
这样，通常的直角坐标系的基底与球坐标系的基底的变换关系为
。
对任意的一个逆变矢量
，在球坐标系之下，可以利用局域活动标架基底和坐标系的基底，有两种展开形式，即
，
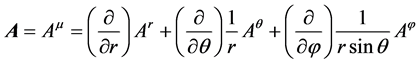。 (12)
类似地，对任意的一个协变矢量
，在球坐标系之下，可以利用局域活动标架基底和坐标系的对偶基底，有两种展开形式，即
，
。
经过以上的讨论和研究，我们知道任何正交曲线坐标系在空间的任何一点都有三组基底来表达和分解一个任意的张量，这三组基底分别为局域活动标架的基底(即通常教科书中的所谓坐标基底)
、对偶坐标基底
和逆变坐标基底
。对不同的正交曲线坐标
系，这三组基底之间的关系会不同，而它们正是求解标量场的梯度、矢量场的散度和旋度时需要考虑的拉梅系数的本质来源。
在柱坐标系情况下，三组基底依次是：
。
它们之间的对应关系为
。 (13)
在球坐标系情况下，三组基底依次是：
。
它们之间的对应关系为
。 (14)
3.2. 梯度、散度和旋度的一般计算公式
在柱坐标系情况下，参考公式(5)，三维空间的线元表达式为：
。 (15)
此时，度规为：
， (16)
度规行列式为：
， (17)
逆变度规为：
。 (18)
由公式(6)，标量场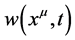
的梯度定义为：
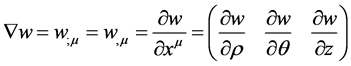。 (19)
考虑到3种基底之间的对应关系式(13)，我们得到标量场
的梯度在柱坐标系中以通常的局域活动标架基底表述的结果为：
。(20)
由公式(7)，矢量场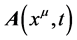
的散度：
，
考虑到公式(11)，我们有
(21)
由公式(8)、(9)，矢量场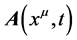
的旋度：
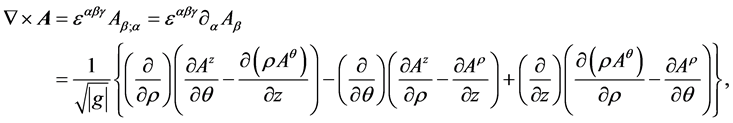
利用公式(13)，进一步整理后，我们有
(22)
由公式(10)，标量场
的拉普拉斯算子为标量，其定义为：
(23)
在球坐标系情况下，参考公式(5)，三维空间的线元表达式为：
。 (24)
此时，度规为：
， (25)
度规行列式为：
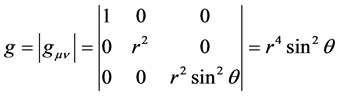， (26)
逆变度规为：
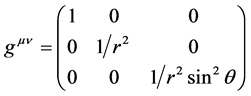。 (27)
由公式(6)，标量场
的梯度定义为：
。(28)
考虑到3种基底之间的对应关系式(14)，我们得到标量场
的梯度在球坐标系中以通常的局域活动标架基底表述的结果为：
。(29)
由公式(7)，矢量场
的散度：
，
考虑到公式(12)，我们有
(30)
由公式(8)、(9)，矢量场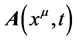
的旋度：
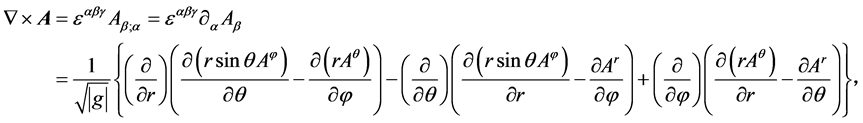
利用公式(14)，进一步整理后，我们有
(31)
由公式(10)，标量场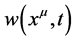
的拉普拉斯算子为标量，其定义为：
(32)
可以看出，上述方法不仅没有机械地引入拉梅系数，而且过程也不再仅仅局限于柱坐标系或球坐标系。只要给定一个线元表达式，确定了在一个坐标系中的度规张量的具体形式，再利用度规张量得到坐标基底和局域活动标架基底之间的关系，由最基本的黎曼几何和张量分析的基础知识，就可以求标量场的梯度和矢量场的散度、旋度。从计算结果可以看出，表达式(20)、(21)、(22)、(23)与用拉梅系数给出的表达式(1)、(2)、(3)、(4)在柱坐标系的具体情况下的结果是完全相符的。同时，表达式(29)、(30)、(31)、(32)与用拉梅系数给出的表达式(1)、(2)、(3)、(4)在球坐标系的具体情况下的结果也是完全相符的。
4. 总结
根据张量分析，标量场的梯度和矢量场的散度、旋度确实不依赖于坐标系，在不同的坐标系下有统一形式的一般求法。我们针对柱坐标系和球坐标系，通过简单的分析，给出了基于度规表达式的计算公式，一般性地解决了标量场的梯度和矢量场的散度、旋度的计算问题。本文的计算，可以帮助我们理解拉梅系数产生的原因，更好地理解和认识梯度、散度和旋度。在实际计算中，不必再死记复杂的拉梅系数。通过对直角坐标系和一般曲线坐标系中结果的分析，澄清了正交曲线坐标系中柱坐标系和球坐标系的基底和对应的局域活动标架基底的关系。
*通讯作者。