基于同态加密域的自适应提升小波

doi:10.12677/CSA.2019.94075

期刊菜单

基于同态加密域的自适应提升小波
Adaptive Lifting Wavelet Scheme Based on Homomorphic Encrypted Domain

DOI: 10.12677/CSA.2019.94075, PDF, HTML, XML,
作者: 吴怡宣^*, 王晅：陕西师范大学，物理学与信息技术学院，陕西西安
关键词: 自适应提升小波；同态加密系统；加密信息处理；Adaptive Lifting Wavelet Scheme； Homomorphic Cryptosystem； Signal Processing in the Encrypted Domain

摘要: 随着信息时代的不断发展，信息安全与隐私保护问题越来越受到人们的重视，由于有价值的信号可能受到恶意攻击，因此它们必须在加密的域中进行处理。本文利用Paillier密码系统的同态特性，对加密域内的待处理信号进行小波分解，提出了一种加密的自适应提升小波方法。此外，还提出了采用加密的LBP方案对细节信号进行编码的方法，这些方法用于服务器在没有私钥的情况下进行数据处理，从而避免敏感信息泄露是非常有用的。我们进行了加密域的重构实验、水印实验和掌纹分类实验，验证了我们提出加密域自适应提升小波的有效性和可行性。

Abstract: With the development of information industry, data privacy’s protection becomes a necessary issue to face with. Since the valuable signals need to be protected from a malicious device, they must be processed in an encrypted domain. In this paper, we proposed an encrypted adaptive lifting wavelet method by using the homomorphic properties of Paillier’s cryptosystem to act wavelet decomposition on pending signal in encrypted domain. In addition, the implementation of encrypted LBP scheme is also proposed to encode detail signal which is prerequisite for classification work. The mentioned works are useful for classification servers to process data without private-key so that the sensitive message will not divulge. We conduct some experiments include reconstruction, simplified watermarking, and palmprint classification experiments in encrypted domain to demonstrate the usefulness and feasibility of our encrypted processing work.

文章引用：吴怡宣, 王晅. 基于同态加密域的自适应提升小波[J]. 计算机科学与应用, 2019, 9(4): 663-673. https://doi.org/10.12677/CSA.2019.94075

1. 引言

随着云计算的诞生与发展，其涉及的信息安全问题越来越受到人们的重视。处理用户的隐私数据成为了信号处理领域的一大热点，且能够实现数据的安全管理、传输、与处理工作变得至关重要。涉及一些个人用于个人身份识别的信息如虹膜、指纹、面部特征等成为研究的热点，相较而言掌纹具有更多的主线、皱纹、脊和细节点等特征，并且拥有非侵入性和高成本效益的优点，我们提出了一种由服务器端在加密状态下对掌纹进行自适应提升小波运算以及特征提取的过程。另外与媒体、版权许可相关的数字水印等信息，作为不可见水印镶嵌入产品时具有隐秘性，作为保护信息安全以及辨别版权真伪的关键信息，数字水印尤其是不可见水印有十分广泛的应用背景，我们所提出的加密信息处理方案同样可以应用于加密水印的嵌入和提取，即服务器端在加密图片上直接嵌入不可见水印，并且可以从中直接提取加密后的水印。在方案的实施过程中，针对可能出现的数据非整数，非正数，数域可能出现扩充等问题进行了研究和探讨，并且介绍了实验过程中必不可少的同态加密域数值比较的方法。

2. Pallier同态加密域

2.1. 同态加密域系统

同态加密系统主要由RSA [1] ，ElGamal [2] ，Paillier [3] 和Damgard-Jurik [4] 等加密算法系统组成，本文所提出的自适应提升小波方案是基于Paillier同态加密域的算法方案。

同态加密系统由Rivest等人提出，利用这样的系统可以在不对信息解密的前提下处理加密后的信息 [5] ，显然地，找出明文和密文之间的代数计算关系是同态加密运算的关键。现有的同态加密系统都有其对应的计算方法变换法则，根据对应变换法则的特点可以将同态加密域分为加法同态加密和乘法同态系统，Pascal Paillier提出的Pailler同态系统具有加法同态性 [3] ，近年来被广泛应用在安全信息处理领域，而针对自适应提升小波原本的计算方法与加法同态的性质，我们选择该加密域进行研究与实验。Paillier加密系统的运算法则在下小节介绍。

2.2. 加密同态性与计算规则

加法同态性可以被描述为明文域的加法运算转换到密文域后变为乘法运算，令 $m_{1}$ 和 $m_{2}$ 表示明文，E[´]表示加密过程，D[´]表示解密过程，{pk, sk}表示一对秘钥，分别对应公钥和私钥，加密算法的加法同态性可以表示为：

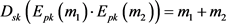(1)

文献 [6] 较详细地介绍了基于第三类陷阱门技术的一种陷阱门机制，它是复合剩余类问题的一种，除了具有加法同态性，该方法同时也具有随机自约性和自束性，因此即使不改变明文也可以得到不同的密文，研究主要用到其加密的过程，这里仅介绍算法计算规则部分。

2.2.1. 秘钥机制

参数p和q为两个大质数并计算它们的乘积，得到N = pq，这样所得到的N很大以至于很难被分解，非零基整数g随机取 $Z_{N^{2}}$ 的子集，使其满足N整除g的阶 $(g \in Z_{N^{2}}^{*})$ ，通常为了方便起见，g可以取值为N + 1。公钥 $λ$ 由g和N共同组成，满足条件： $λ = l c m (p - 1, q - 1)$ ，式中l cm代表最小公倍数。

2.2.2. 加密过程

规定明文m的范围为m < N，之后随机选取一个整数r < N，可以得到加密运算过程为：

$E_{p k} (m) = g^{m} \cdot r^{N} \mod N^{2} = c$ (2)

其中c表示密文 $c \in Z_{N^{2}}^{*}$ 。

2.2.3. 解密过程

令密文满足c < N²，明文m可以根据以下公式计算得到：

$D_{s k} (c) = \frac{L (c^{λ} \mod N^{2})}{L (g^{λ} \mod N^{2})} \mod N = m$ (3)

其中 $L (x) = (x - 1) / N$ 。

特别地，根据公式(2)和(3)我们可以得到以下关系式：

$D_{s k} (E_{p k} (m_{1}) E_{p k} (m_{2}) \mod N^{2}) = m_{1} + m_{2} \mod N$ (4)

$D_{s k} (E_{p k} (m_{1}) E_{p k} {(m_{2})}^{- 1} \mod N^{2}) = m_{1} - m_{2} \mod N$ (5)

$D_{s k} (E_{p k} {(m)}^{k} \mod N^{2}) = k m \mod N$ (6)

3. 同态加密特征提取算法

上小节对Paillier同态加密过程进行了基本算法介绍，本节在此基础上提出了相应的同态加密域下的自适应提升小波和LBP策略，在研究过程中同样关注了同态加密域的数值比较问题。

3.1. 同态自适应提升小波方案

通过对自适应提升小波算法的运算过程进行分析 [7] ，结合Paillier加密系统的加法同态性，我们提出了在同态加密域内实现该方案的具体方法：

首先，用户对大小为 $N \times M$ 原明文图像函数 $f (x, y)$ 按照公式(2)进行加密运算，之后得到相同大小的加密后图像 $f_{e} (x, y)$ (下标“e”表示加密域的参数，下文中出现同样适用)，将其传送给服务器端后，服务器端在加密的情况下对密文进行相应的小波运算，特征提取等处理攻错。与传统提升小波的计算过程相类似的，本方案的准备工作为图像的像素奇偶位置重组，我们将从 $f_{e} (x, y)$ 分离得到4个密文图像子块：

$x_{e} (n, m) = f_{e} (2 n, 2 m)$ ， $y_{e h} (n, m) = f_{e} (2 n - 1, 2 m)$ ， $y_{e v} (n, m) = f_{e} (2 n, 2 m - 1)$ ， $y_{e d} (n, m) = f_{e} (2 n - 1, 2 m - 1)$ 。为使该方案在明文域得到二值决策矩阵 $D (n, m)$ ，八个方向相邻像素均值和偏差值关系表，需要经过以下的运算过程：

$μ = \frac{1}{8} [y_{h} (n - 1, m) + y_{h} (n, m) + y_{v} (n, m) + y_{v} (n, m - 1) + y_{d} (n - 1, m) + y_{d} (n, m) + y_{d} (n, m - 1) + y_{d} (n - 1, m - 1)]$ (7)

$\begin{array}{l} σ (n, m) = | y_{h} (n - 1, m) - μ | + | y_{h} (n, m) - μ | + | y_{v} (n, m - 1) - μ | \\ + | y_{v} (n, m) - μ | + | y_{d} (n - 1, m) - μ | + | y_{d} (n, m - 1) - μ | \\ + | y_{d} (n, m) - μ | + | y_{d} (n - 1, m - 1) - μ | \end{array}$ (8)

在公式(7)和(8)的基础上可以得到二值决策阵 $D (n, m)$ 的算法：

$D (n, m) = {\begin{matrix} 0 & σ (n, m) > T \\ 1 & σ (n, m) \leq T \end{matrix}$ (9)

其中T为阈值我们可以根据具体情况和需要进行调整。

近似信号 $x^{'} (n, m)$ 被定义为：

$x^{'} (n, m) = {\begin{matrix} x (n, m) & D (n, m) = 0 \\ \frac{1}{2} [x (n, m) + U] & D (n, m) = 1 \end{matrix}$ (10)

其中U为更新因子，被定义为：

$U = \frac{1}{4} [y_{h} (n - 1, m) + y_{h} (n, m) + y_{v} (n, m - 1) + y_{v} (n, m)]$ (11)

预测参数可以根据以下公式得到：

$p_{h} (n, m) = \frac{1}{2} [x^{'} (n - 1, m) + x^{'} (n, m)]$ (12)

$p_{v} (n, m) = \frac{1}{2} [x^{'} (n, m - 1) + x^{'} (n, m)]$ (13)

$p_{d} (n, m) = \frac{1}{2} [x^{'} (n - 1, m - 1) + x^{'} (n, m)]$ (14)

根据上述的公式，细节信号参数 ${y^{'}}_{h}$ ， ${y^{'}}_{v}$ 和 ${y^{'}}_{d}$ 可以被定义为：

${y^{'}}_{h} (n, m) = | y_{h} (n, m) - p_{h} (n, m) |$ (15)

${y^{'}}_{v} (n, m) = | y_{v} (n, m) - p_{v} (n, m) |$ (16)

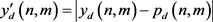(17)

求得估计信号 $x^{'} (n, m)$ 和细节信号参数 ${y^{'}}_{h}$ ， ${y^{'}}_{v}$ 和 ${y^{'}}_{d}$ 的过程包括了四则运算和绝对值运算，显然如果我们对整数进行加减乘运算并不会得到带小数的结果，但是从公式(7)~(17)可以看出，计算过程中同样包含了除法运算，因此我们无法确保计算结果都是整数，公式(9)包含了绝对值运算和两个数之间比较大小的问题，上述提到的运算在明文域进行都是十分方便的，但由于同态加密域中所有参与运算的参数和数据必须以整数形式表达出来这一特点，在同态加密系统中完成上述运算是一项重要且艰巨的挑战。

基于从加密后图像 $f_{e} (x, y)$ 分离出来的子图像 $y_{e h} (n, m)$ ， $y_{e v} (n, m)$ 和 $y_{e d} (n, m)$ ，通过对 $σ (n, m)$ 和T值扩大8倍的运算，我们可以得到同态加密域下的二值决策矩阵 $D_{e}$ (实际上与明文域下的D相同)。具体方法如下：令 $y_{e h 8} (n, m) = y_{e h}^{Q} (n, m)$ ， $y_{e v 8} (n, m) = y_{e v}^{Q} (n, m)$ ， $y_{e d 8} (n, m) = y_{e d}^{Q} (n, m)$ 其中Q = 8，再根据式(4)~式(8)，可推导出如下计算公式：

$μ_{e} = y_{e h 8} (n - 1, m) \times y_{e h 8} (n, m) \times y_{e v 8} (n, m) \times y_{e v 8} (n, m - 1) \times y_{e d 8} (n - 1, m) \times y_{e d 8} (n, m) \times y_{e d 8} (n, m - 1) \times y_{e d 8} (n - 1, m - 1)$ (18)

$\begin{array}{l} σ_{e} (n, m) = {| y_{e h 8} (n - 1, m) - μ_{e} |}_{e} \times {| y_{e h 8} (n, m) - μ_{e} |}_{e} \times {| y_{e v 8} (n, m - 1) - μ_{e} |}_{e} \\ \times {| y_{e v 8} (n, m) - μ_{e} |}_{e} \times {| y_{e d 8} (n - 1, m) - μ_{e} |}_{e} \times {| y_{e d 8} (n, m - 1) - μ_{e} |}_{e} \\ \times {| y_{e d 8} (n, m) - μ_{e} |}_{e} \times {| y_{e d 8} (n - 1, m - 1) - μ_{e} |}_{e} \end{array}$ (19)

其中，加密域下的绝对值运算 ${| x_{1} - x_{2} |}_{e}$ 可以被表示为：

${| x_{1} - x_{2} |}_{e} = {\begin{matrix} x_{1} \cdot x_{2}^{- 1} & x_{1} \geq x_{2} \\ x_{2} \cdot x_{1}^{- 1} & x_{1} < x_{2} \end{matrix}$ (20)

式中的 $x_{n}^{- 1}$ 表示 $x_{n}$ 的模逆。

同态加密域的二值决策矩阵 $D_{e} (n, m)$ 被定义为：

$D_{e} (n, m) = {\begin{matrix} 0 & σ_{e} (n, m) > T_{e} \\ 1 & σ_{e} (n, m) \leq T_{e} \end{matrix}$ (21)

其中 $T_{e} = E {(T, r)}^{8} \mod N^{2}$ 。如果将所有参数同时扩大相同倍数，他们的数值之间的大小关系并不会发生改变，进行这样运算相当于扩充了仅是为了确保加密域下的所有参数为整数，因此不难得知 $D_{e} (n, m)$ 与 $D (n, m)$ 的值实际上是相同的。本文的3.3小节对同态比较方法进行了介绍。

为了在随后的计算过程中同样避免小数的产生，该运算过程中需要首先将明文域原图像素扩大16倍，并根据公式(4)~(6)的同态法则将相应的运算过程转换至密文域中。当从密文图像 $f_{e} (x, y)$ 求得决策矩阵 $D_{e} (n, m)$ 之后，可以得到同态加密域下的近似信号 ${x^{'}}_{e} (n, m)$ 为：

${x^{'}}_{e} (n, m) = {\begin{matrix} E {(x (n, m))}^{16} \mod N^{2} & D_{e} (n, m) = 0 \\ E {(x (n, m))}^{8} \times E {(U_{4})}^{2} \mod N^{2} & D_{e} (n, m) = 1 \end{matrix}$ (22)

其中 $U_{4} = y_{e h} (n - 1, m) \times y_{e h} (n, m) \times y_{e v} (n, m - 1) \times y_{e v} (n, m)$ ，原计算公式(12)~(17)可以按法则转换到同态加密系统下，依次为：

$p_{e h} (n, m) = {x^{'}}_{e} (n - 1, m) \times {x^{'}}_{e} (n, m)$ (23)

$p_{e v} (n, m) = {x^{'}}_{e} (n, m - 1) \times {x^{'}}_{e} (n, m)$ (24)

$p_{e d} (n, m) = {x^{'}}_{e} (n - 1, m - 1) \times {x^{'}}_{e} (n, m)$ (25)

${y^{'}}_{e h} (n, m) = {| y_{e h}^{Q} (n, m) - p_{e h} (n, m) |}_{e}$ (26)

${y^{'}}_{e v} (n, m) = {| y_{e v}^{Q} (n, m) - p_{e v} (n, m) |}_{e}$ (27)

${y^{'}}_{e d} (n, m) = {| y_{e d}^{Q} (n, m) - p_{e d} (n, m) |}_{e}$ (28)

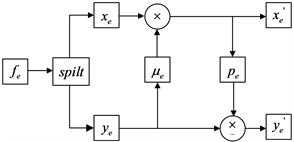
其中，式(26)~(28)中的Q = 16。为了在加密域直接进行图像重构，根据式(26)~(28)中绝对值运算的过程，需要保留运算过程中的数值大小关系矩阵 $C_{e h} (n, m)$ ， $C_{e v} (n, m)$ 和 $C_{e d} (n, m)$ 。图1(a)，图1(b)分别给出了加密域下的自适应提升小波运算步骤和其逆运算的步骤。

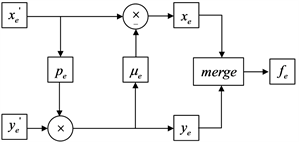(a) (b)

Figure 1. (a) Lifting scheme in encrypted domain; (b) Reversed scheme in encrypted domain

图1. (a)加密提升小波方案；(b)加密小波逆运算方案

3.2. 同态加密LBP方案

LBP (local binary patterns)是一种局部特征算子，近年来被广泛应用于图像的识别工作当中 [8] [9] [10] ，LBP算法的基本思想是：将图片分成数个小区域，选区每个区域中的中心点像素的灰度值作为一个阈值，取中心点邻近像素的值与阈值进行对比，根据比较的结果对图像像素进行某种规则的编码。图2是中心

像素与其邻近像素的示意图，其中 $x_{c}$ 表示中心像素， $x_{p}, (p = 0, 1, \dots p - 1)$ 为邻近像素，这里选取径向距

离R = 1，p = 8，表示编码方式考虑8个不同方向，由此，每个中心像素点的编码过程可以表示如下：

$L B P_{p, R} = \sum_{p = 0}^{p - 1} s (x_{p} - x_{c}) \cdot 2^{p}$ (29)

其中，门限函数 $s (x) = {\begin{matrix} 1 & x \geq 0 \\ 0 & x < 0 \end{matrix}$ [11] ，大于等于中心点像素则赋值为1，小于则赋0值，编码顺序可以

采取顺时针或逆时针任意一种形式，并根据公式进行加权求和运算得到直方图，保留直方图中的有效数据作为特征向量进行接下来的识别工作。

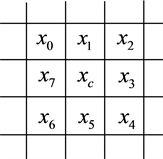
Figure 2. The neighbor sets for p = 8, R = 1in clockwise

图2. p= 8，R = 1相邻像素顺时针编码示意图

要在加密域进行LBP运算的核心问题依然是同态加密域下的两个数值比较大小的问题，3.3节详细介绍了所要用到的同态加密域下的比较大小策略，在我们用该方法求出加密域的 $s (x)$ 的值后，式(29)依旧可以用相同的形式来计算密文图像没一个中心像素的LBP值。

3.3. 同态数值比较策略

对于加密域两个密文数值大小比较： $c_{1} = E (m_{1}, r_{1})$ ， $c_{2} = E (m_{2}, r_{2})$ ，用户需要发送 $c_{1}$ ， $c_{2}$ 至服务器，并且将密文域从0到 $N^{2} - 1$ 划分为k个区间，区间的个数取决于用户在明文域的门限设置 $T_{i} \in Z_{n}$ 。用户需要首先将数个门限值 $T_{i}$ 进行加密为 $T_{e i}^{u}$ ：

$T_{e i}^{u} = E (T_{i}, r_{u}) = g^{T i} r_{u}^{N} \mod N^{2}$ (30)

其中r_u分别等于r₁和r₂， $i = 1, 2, 3 \dots, k$ 。根据文献 [8] ，同态比较的原则是找到加密数据在整个数据段中

的位置，即被 $T_{e i}^{u}$ 分段后所处的段位，根据公式(4)不难得出， $E (m_{u}, r_{u}) \cdot E (I n c, r_{s}) = E (m_{u} + I n c, r_{u} \cdot r_{s})$ 可以通过计算逐步步长Inc接近门限 $T_{e i}^{u}$ 来得到。很明显， $m_{u}$ 与 $T_{e i}^{u}$ 之间的距离可以通过给 $E (m_{u}, r_{u})$ 逐步乘 $E (1, 1)$ 直到 $E (m_{u} + I n c, r_{u}) = T_{e i}^{u}$ ， $(i = 1, 2 \dots, k)$ 这样的方式来进行度量。具体的比较策略如下：

$(s_{u}, d_{u}) = \underset{i, I n c}{\arg \min} (E (T_{i}, r_{u}) - E (m_{u}, r_{u}) g^{I n c})$ (31)

其中s_u表示与密文c_u数值上最接近的门限值，d_u衡量了与最接近的门限值之间的距离，因此通过两个密文我们可以得到两组数据 $(s_{1}, d_{1})$ 和 $(s_{2}, d_{2})$ ，密文c₁和c₂之间的数值大小关系比较方法为：如果s₁ > s₂，则c₁ > c₂；如果s₁ < s₂，则c₁ < c₂，如果得到的结果是s₁ = s₂，则比较的结果取决于d_u的值：

${\begin{array}{l} i f & d_{1} > d_{2} & h e n & c_{1} < c_{2} \\ i f & d_{1} < d_{2} & h e n & c_{1} > c_{2} \\ i f & d_{1} = d_{2} & h e n & c_{1} = c_{2} \end{array}$ (32)

以上介绍的同态数值大小的比较方法可以用于加密系统的绝对值运算，LBP运算，以及后续实验中要将用到的K近邻分类方法的计算过程中。

4. 仿真实验

4.1. 重构实验

图3(a)为大小为512 × 512的灰度图像“peppers”作为我们重构实验的原图像信号，用两个大质数将其加密之后并按照2.1节提出的加密提升小波算法进行处理，并且按照公式(18)~(28)的逆运算逐步进行图像的重构过程，这里不重复介绍逆运算的细节，图3(a)~(d)分别展示了原图像，加密后的图像，重构后的加密图像以及解密后的重构图像，实验过程中MIM方案 [12] 用于减少数域的扩充问题，也就是在运算中利用MIM进行数据的除法运算，从而消除了扩张因子Q对数域扩充的影响。从图3(a)和图3(d)我们可以看出，两张图片在相同位置具有相同的像素值，这意味着解密后的重构图像与原图像完全相同，整个加密重构过程并没有出现失真的问题。

(a) (b) (c) (d)

Figure 3. (a) Original gray-scale image; (b) Encrypted image; (c) Reconstruction image; (d) Decryption of reconstruction image

图3. (a) 原灰度图像；(b) 加密后的灰度图像；(c) 加密域重构图像；(d) 解密的重构图像

4.2. 水印实验

利用我们提出的自适应提升小波策略，同样在加密域进行了图像的水印实验，本次实验采用了文献 [13] 中所介绍的水印嵌入方式，嵌入水印的公式为：

${v^{'}}_{i} = v_{i} + α w_{i}$ (33)

其中，v_i表示原图像信号，w_i为需要嵌入的水印信号，选取如图4(a)所示的陕西师范大学校徽二值图像，大小为128 × 128像素作为水印信号进行实验，参数α是从{1, 2, …, k}中随机选取的一个小整数，为适当简化加密域中的水印运算，这里我们取α = 2。值得注意的是，在实验中一般将不可见水印嵌入中频信号中以减少对原宿主图片的影响，即v_i表示图片的中频信号。因此，将原图进行两次小波分解之后，将水印信号w_i嵌入第二次分解的高频信号中，此时的高频信号对于原图像来说相当于其中频信号。

根据同态加密域的性质，水印嵌入公式(33)被改写为以下的加密形式：

$E ({v^{'}}_{i}) = E (v_{i}) E {(w_{i})}^{α}$ (34)

(a) (b) (c)

Figure 4. (a) School badge as watermarking signal; (b) The extracted watermark in plaintext domain; (c) The extracted watermark in encrypted domain

图4. (a) 校徽水印图像；(b)从明文中提取的水印图像；(c) 从密文中提取的水印图像

为了避免在水印嵌入后的重构过程中出现非整数运算，经实验验证量化因子 $Q = 2^{7}$ 可以保证水印嵌入和提取过程中的可行性，图5(a)是已嵌入水印的加密图像，图5(b)是解密后的含水印图像，实验过程中同样采取了MIM方法来避免数域的扩充。

(a) (b)

Figure 5. (a) Encrypted version of watermarked image; (b) Decryption of watermarked image

图5. (a) 已嵌入水印的加密图像；(b) 解密含水印图像

由于嵌入的水印图像为二值图像，为了确保提取出的水印像素值仅由整数构成，我们采用了门限比较方案如式(35)所示从宿主图像中提取水印图像。

$w_{i} = {\begin{matrix} 1 & D [E ({v^{'}}_{i}) E {(v_{i})}^{- 1}] > T \\ 0 & D [E ({v^{'}}_{i}) E {(v_{i})}^{- 1}] \leq T \end{matrix}$ (35)

其中，由多次实验选取合适的门限值T。图4(b)，图4(c)分别展示了从明文图像提取出来的水印图像和从密文图像中提取的水印图像。我们分别采用PSNR和归一化相关系数(NC) [6] 来衡量提取水印的保真度和测量明文域和密文域提取水印信号与原水印信号的相似度。实验结果见表1。

Table 1. The watermarking embedded and extracted performances in terms of PSNR and NC

表1. 水印实验PSNR值和NC值

通过实验结果可以看出，加密域的水印嵌入和提取实验结果与直接在明文域进行的结果几乎可以达到近似的结果，说明了我们所提出方案的可行性与保真性。

4.3. 掌纹识别实验

在本小节，针对香港理工大学掌纹数据库Poly-II [14] 进行了加密系统的掌纹识别实验，该数据库由两大部分组成，包含了193个人的共386个掌纹图片，总数为7720张大小为384 × 284的掌纹灰度图像，两部分图像由两次采集组成，平均时间间隔相差了69天，每次分别针对同一个手掌图片采集十张照片，二次采集过程中相机的焦点和光源不同，因此可以看成是由不同的掌纹采集设备所得到的数据集。

4.3.1. 实验一

本实验目的主要在于比较提出的加密算法和其明文域算法对于掌纹识别工作的准确性。由于在加密域中反复进行同态比较运算需要大量的计算时间，因此从该数据库的每部分中随机抽取了500张图片进行实验。分别以第一部分和第二部分十张图片中的前五张作为训练样本构成训练集，后五张作为测试样本，图6列举出了一些数据库的样本示例。实验提取特征的过程为：将每张图片加密后实施加密域自适应提升小波方案，得到一张近似图像和三张细节图像，再通过加密域LBP算法将每张细节图像转换为二进制编码的形式得到图像特征，在此基础上利用K近邻分类的方法对数据进行分类，表2分别列出了明文掌纹图片和加密条件下的掌纹图片进行分类的结果。

Figure 6. Few samples of palmprint database

图6. 部分掌纹数据库图片

Table 2. CCPs of palmprints in plaintext and encrypted domain

表2. 明文域与加密域下的掌纹识别性能

从表2可以看出，本文所提出的方案在加密数据集下进行实验，与明文条件下直接进行小波运算并提取特征再分类的识别率几乎相同，并没有因为加密过程对图像像素造成的混乱而影响识别精度，即保证了信息安全的同时也可以完成相应的识别任务。

4.3.2. 实验二

本实验的目的在于验证加密算法下的识别工作对不同聚焦光照条件下的掌纹识别工作的鲁棒性。本次实验从每部分随机抽取250张图片，两部分共500张图片，第一部分十张图片的前五张作为训练样本，第二部分的前五张作为训练样本，对样本进行加密后用本章提出的方法进行特征提取工作，与此同时，Pan [15] ，Kong [16] ，2D-Gabor小波 [17] ，以及传统的主成分分析 [18] ，线性判别分析 [19] 的方法也在这里与我们的方法进行了比较，表3分别列出了这些方法分别针对明文掌纹图像和加密掌纹图像下的识别率。

Table 3. Pattern classification percentage on the original database and encrypted palmprint with various methods

表3. 多种方法下的明文数据与加密数据分类正确率

通过实验结果可以看出，我们提出的方法在明文数据集下具有更好的分类性能，而在应用于加密数据上，由于加密过程造成的掌纹结构与纹理信息的混乱，导致传统方法的识别过程无法得到需要的高精度的识别结果，而我们提出的方案由于其应用于加密域时所具有的无损的性质，从而在加密的样本数据上依然保持了与明文域等同的正确识别率，这样可以得出结论是，我们的算法在加密域中具有鲁棒性，可以应用于隐私保护相关领域的识别工作。

5. 总结

本文提出了一种无精度损失的Pallier加密域自适应提升小波的实现方案，在此基础上同样提出了加密域LBP的实现方法。基于Paillier同态加密系统的性质与特点与原有的自适应提升小波思想，我们科学合理推导了其在加密域的计算公式，并给出了相关扩张因子的大小以确保计算过程无误差地进行。相较于已有的其他加密系统的SIFT，DCT等图像变换方法，我们所提出的方案通过准确扩大像素的倍数以及通过采用相对较小的扩张因子，使加密域数据的计算更加精确。相关实验分别验证了其在图像重构、水印嵌入提取和掌纹识别方面都具有良好的应用前景，即保证了敏感隐私信息的安全性，也完成了相应的图像信息处理任务。

致谢

在此感谢王晅导师对我研究选题方向以及科研过程中的指导，感谢杨腾飞师兄对本次论文实验方面的帮助，同时感谢实验室同学日常与我共同探讨学术问题以及在我遇到困难时伸出援助之手。

参考文献

参考文献

[1]	[1] Rivest, R., Shamir, A. and Adleman, L. (1978) A Method for Obtaining Digital Signatures and Public-Key Cryptosys-tems. Communications of the ACM, 21, 120-126. https://doi.org/10.1145/359340.359342
[2]	Elgamal, T. (1985) A Public-Key Cryptosystems and a Signature Scheme Based on Discrete Logarithms. IEEE Transactions on Information Theory, 31, 469-472. https://doi.org/10.1109/TIT.1985.1057074
[3]	Paillier, P. (1999) Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. International Conference on the Theory and Application of Crypto-graphic Techniques, Prague, 2-6 May 1999, 223-238. https://doi.org/10.1007/3-540-48910-X_16
[4]	Damgard, I. and Jurik, M. (2001) A Generalization, a Simplifica-tion and Some Application of Paillier’s Probabilistic Public-Key System. 4th International Workshop on Practice and Theory in Public Key Cryptography, Cheju Island, 13-15 February 2001, 119-136. https://doi.org/10.1007/3-540-44586-2_9
[5]	Rivest, R., Adleman, L. and Dertouzos, M. (1978) On Data Banks and Privacy Homomorphisms. In: DeMillo, R.A., et al., Eds., Foundations of Secure Computation, MIT Press, Cam-bridge, 169-178.
[6]	Run, R.S., Horng, S.J., Lai, J.L., Kao, T.W. and Chen, R.J. (2012) An Improved SVD-Based Watermarking Technique for Copyright Protection. Expert Systems with Applications, 39, 673-689. https://doi.org/10.1016/j.eswa.2011.07.059
[7]	Wang, X., Liang, J.H. and Wang, M.Z. (2013) On-Line Fast Palmprint Identification Based on Adaptive Lifting Wavelet Scheme. Knowledge-Based Systems, 42, 68-73. https://doi.org/10.1016/j.knosys.2013.01.013
[8]	Hsu, C.H., Lu, C.S. and Pei, S.C. (2012) Image Feature Extrac-tion in Encrypted Domain with Privacy-Preserving SIFT. IEEE Transactions on Image Processing, 21, 4593-4607. https://doi.org/10.1109/TIP.2012.2204272
[9]	Dalali, S. and Suresh, L. (2016) Daubechive Wavelet Based Face Recognition Using Modified LBP. Procedia Computer Science, 93, 344-350. https://doi.org/10.1016/j.procs.2016.07.219
[10]	Yang, W.K., Wang, Z.Y. and Zhang, B.C. (2016) Face Recogni-tion Using Adaptive Local Ternary Patterns Method. Neurocomputing, 213, 183-190. https://doi.org/10.1016/j.neucom.2015.11.134
[11]	Ojala, T., Pietikäinen, M. and Mäenpää, T. (2002) Multiresolu-tion Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24, 971-987. https://doi.org/10.1109/TPAMI.2002.1017623
[12]	Zheng, P.J. (2013) Student Member, Discrete Wavelet Trans-form and Data Expansion Reduction in Homomorphic Encrypted Domain. IEEE Transactions on Image Processing, 22, 2455-2468. https://doi.org/10.1109/TIP.2013.2253474
[13]	Cox, I., Kilian, J., Leighton, F. and Shamoon, T. (1997) Secure Spread Spectrum Watermarking for Multimedia. IEEE Transactions on Image Processing, 6, 1673-1687. https://doi.org/10.1109/83.650120
[14]	Zhang, D., Kong, A., You, J. and Wong, M. (2003) Online Palmprint Iden-tification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 25, 1041-1050. https://doi.org/10.1109/TPAMI.2003.1227981
[15]	Pan, X. and Ruan, Q.Q. (2008) Palmprint Recognition Using Gabor Feature-Based (2D) 2 PCAJ. Neurocomputing, 71, 3032-3036. https://doi.org/10.1016/j.neucom.2007.12.030
[16]	Kong, W.K., Zhang, D. and Li, W. (2003) Palmprint Feature Extraction Using 2-D Gabor Filters. Pattern Recognition, 36, 2339-2347. https://doi.org/10.1016/S0031-3203(03)00121-3
[17]	Wang, X., Lei, L. and Wang, M. (2012) Palmprint Verifica-tion Based on 2D-Gabor Wavelet and Pulse-Coupled Neural Network. Knowledge-Based Systems, 27, 451-455. https://doi.org/10.1016/j.knosys.2011.10.008
[18]	Wu, X., Zhang, D. and Wang, K. (2003) Fisherpalms Based Palmprint Reconition. Pattern Recognition Letters, 24, 2829-2838. https://doi.org/10.1016/S0167-8655(03)00141-7
[19]	Lu, G., Zhang, D. and Wang, K. (2003) Palmprint Recogni-tion Using Eigenpalms Features. Pattern Recognition Letters, 24, 1463-1467. https://doi.org/10.1016/S0167-8655(02)00386-0

为你推荐

友情链接