摘要:
运用锥上的不动点定理获得了半正二阶三点边值问题
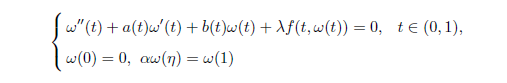
正解的存在性结果,其中λ > 0, 0 < η < 1 且满足 0 < αη < 1,f∈C([0,1]×[0,∞),(−∞, ∞))存在正常数 M 使得f(t,ω)≥−M 成立。
Abstract:
By using the fixed-point theorem in cones, we obtain the existence of positive solutions for the semi-positive second-order three-point boundary value problems
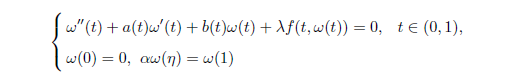
where λ > 0, 0 < η < 1 satisfies 0 < αη < 1 and f∈C([0,1]×[0,∞),(−∞,∞)), with f(t,ω)≥−M for some positive constants M.