预测不同放牧策略对草原土壤的影响

Predict the Effects of Different Grazing Strat-egies on Grassland Soils

摘要: 本文对不同放牧策略对植被生物量、土壤湿度、土壤有机物含量进行评价分析，从降水量、土壤蒸发等数据进行时间序列预测土壤湿度，从草原监测点历史监测土壤数据建立拟合预测不同放牧强度下的土壤有机物含量预测，得出一个放牧的最优策略，促进了草原的可持续发展。首先，从机理分析的角度建立熵权Topsis综合评价模型，分别评价不同的放牧策略对植被生物量和不同放牧强度对土壤湿度的影响。然后，使用基于时间序列的随机森林预测模型，预测2022年4月到2023年12月不同深度的土壤湿度。最后，从机理分析的角度出发建立基于专家权重的Topsis综合评价法，评价不同放牧策略对土壤化学性质的影响，然后结合附件相关数据，使用基于时间序列的多层LSTM模型进行预测在不同放牧强度下的2022年同期的一些有机碳、无机碳、全N和C/N比等值。

Abstract: In this paper, different grazing strategies evaluate and analyze vegetation biomass, soil moisture and soil organic matter content, predict soil moisture in time series from precipitation and soil evaporation data, establish a fitting prediction of soil organic matter content under different graz-ing intensities from the historical monitoring soil data of grassland monitoring points, and obtain an optimal grazing strategy, which promotes the sustainable development of grassland. Firstly, from the perspective of mechanism analysis, a comprehensive evaluation model of entropy weight Topsis is established, and the effects of different grazing strategies on vegetation biomass and different grazing intensities on soil moisture are evaluated respectively. Then, using a time-series-based random forest forecasting model, soil moisture at different depths from April 2022 to December 2023 is forecasted. Finally, from the perspective of mechanism analysis, the Topsis comprehensive evaluation method based on expert weighting is established to evaluate the effects of different grazing strategies on soil chemical properties, and then combined with the relevant data of attach-ments, a multi-layer LSTM model based on time series is used to predict some organic carbon, inor-ganic carbon, total N and C/N ratios in the same period of 2022 under different grazing intensities.

1. 引言

关于草原放牧通常要考虑放牧方式和放牧强度(单位面积牲畜密度) 2个因素。植物的生长满足自身的生长规律，同时受到周围环境的影响。例如，降水、温度、土壤湿度、土壤PH、营养等都决定植物的生长情况。当牧羊对植物进行采食时，一方面植物的地上生物量减少；另一方面，放牧对植物有刺激作用，改变了植物原有的生长速率，适当的放牧会刺激植物的超补偿生长，同样不合理的放牧也会降低植物的生长速率。

过度放牧，往往因牲畜密度过大，可能导致草原植被结构破坏，土壤裸露面积增大，促进了土壤表面的蒸发，土体内水分相对运动受到不利影响，破坏了土壤积盐与脱盐平衡，增加了盐分在土壤表面的积累，土壤盐碱化程度加重，最终造成草场退化、土地沙漠化。土壤沙漠化又被称为沙质沙漠化，是荒漠化的一种主要表现类型。沙漠化是在干旱、半干旱和部分半湿润地区的沙物质基础和干旱大风动力条件下，由于自然因素或人为活动的影响，致使自然的生态系统平衡性遭到破坏的现象。

适度的放牧可以改善草原土壤质量、提高草原生物的多样性。一方面由于家畜的采食践踏造成枯落物分解，充分进入土壤，从而提高土壤有机质和氮和钾含量，减少土壤的板结。另一方面放牧能够降低表层土壤湿度、PH，一定程度增加土壤容重。有研究表明：高寒草甸的土壤全氮含量沿着放牧梯度呈下降趋势。因此，为了保证土壤达到合适的状态，找到放牧羊(标准羊)数量的阈值是问题的关键。

根据我国草地资源的经营现状，开展草地放牧系统优化模型研究具有重要意义。现代草地资源的经营应遵循可持续利用原则，在保证生态环境良性健康发展中寻求经济利益的最大化。草地放牧系统优化模型的建立可以综合考虑各方面因素。因此，我们希望站在可持续发展和可承载范围的角度，并利用模型准确预测草原放牧合理强度，从而大大提高草原的生态环境，带动区域经济发展 [1] [2]。

2. 不同放牧策略对草原土壤物理性质和植被生物量的影响

近年来由于不合理的家畜放牧已经引起了草原植被生物量及草原物理性质的严重影响，带来了生物多样性的丧失。阐明放牧影响下草原群落的多样性变化规律，探讨其变化机理，是草原生物资源合理利用的基础。主要从机理的角度出发，建立数学模型，通过熵权法加Topsis法组成一个综合评价模型，建立对土壤湿度和植被生物量相关的数学模型，从机理上评判在不同放牧策略下产生的影响。

2.1. 熵权Topsis法

1) 正向化以及标准化处理。判断输入的矩阵是否存在负数，如果有则要重新标准化到非负区间，将评价对象个数的最大值用n表示，m个评价指标构成的正向化矩阵如下 [3]：

$X=\left[\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ ⋮& ⋮& ⋮\\ x_{n1}& x_{n2}& x_{n3}\end{array}\right]$ (1)

那么，对其标准化的矩阵记为Z，Z中的每个元素：

$z_{ij}=x_{ij}/\sqrt{{\displaystyle {\sum }_{i=1}^n{x}_{ij}^2}}$ (2)

判断Z矩阵中是否存在着负数，如果存在的话，需要对X使用另一种标准化方法，对矩阵X进行一次标准化得到矩阵，其标准化的公式为

$z_{ij}=\frac{x_{ij}-\left\{x_{1j},x_{2j},\cdots ,x_{nj}\right\}}{\max \left\{x_{1j},x_{2j},\cdots ,x_{nj}\right\}-\min \left\{x_{1j},x_{2j},\cdots ,x_{nj}\right\}}$ (3)

2) 计算概率矩阵。计算第j项指标下第i个样本所占比重，并将其看作相对熵计算中用到的概率，假设有n个要评价的对象，m个评价指标，经过了上一步处理得到的非负矩阵为

$Z=\left[\begin{array}{cccc}{z}_{11}& z_{12}& \cdots & z_{1n}\\ z_{21}& z_{22}& \cdots & z_{2n}\\ z_{n1}& z_{n2}& \cdots & z_{nn}\end{array}\right]$ (4)

计算概率矩阵P，其中P中每一个元素P_ij的计算公式如下：

$P_{ij}=\frac{Z_{ij}}{{\displaystyle {\sum }_{i=1}^n{z}_{ij}}}$ (5)

容易验证 ${\displaystyle {\sum }_{i=1}^n{p}_{ij}}=1$，即保证了每一个指标所对应的概率之和为1。

3) 计算每个指标的信息熵，并计算信息效用值，并归一化得到每个指标的熵权

对于第j个指标而言，其信息熵的计算公式为：

$e_j=-\frac{1}{Inn}{\displaystyle {\sum }_{i=1}^n{P}_{ij}In\left(P_{ij}\right)}\left(j=1,2,\cdots ,m\right)$ (6)

4) 计算得分并归一化。上述熵权法步骤已经完成了原始矩阵正向化和正向化矩阵标准化，此处不再处理，仅使用了TOPSIS中计算得分与归一化。

n个要评价对象，m个评价指标的标准化矩阵：

$Z=\left[\begin{array}{cccc}{z}_{11}& z_{12}& \cdots & z_{1n}\\ z_{21}& z_{22}& \cdots & z_{2n}\\ z_{n1}& z_{n2}& \cdots & z_{nn}\end{array}\right]$ (7)

Z_ij表示i个同学的第j个指标，定义最大值 $Z^{+}$ 和最小值 $Z^{-}$。

定义第i ( $i=1,2,\cdots ,n$ )个评价对象与最大值的距离：

$D_i^{+}=\sqrt{{\displaystyle {\sum }_{j=1}^m{\omega }_j}{\left(Z_j^{-}-Z_{ij}\right)}^2}$ (8)

定义第i个评价对象与最小值之间的距离：

$D_i^{-}=\sqrt{{\displaystyle {\sum }_{j=1}^m{\omega }_j}{\left(Z_j^{+}-Z_{ij}\right)}^2}$ (9)

那么，我们可以计算得出第i ( $i=1,2,\cdots ,n$ )个评价对象未归一化的得分：

$S_i=\frac{D_i^{-}}{D_i^{+}+D_i^{-}}$ (10)

很明显 $0\le S_i\le 1$，且 $S_i$ 越大 $D_i^{+}$ 越小，即越接近最大值。然后对得分进行归一化处理(这一列的每个元素除以该列元素总和)，然后得到第i个评价对象的最终得分。

2.2. 计算结果

2.2.1. 不同放牧强度对植被生物量的影响

计算结果如下表1所示。

Table 1. Effects of different grazing intensities on vegetation biomass

表1. 不同放牧强度对植被生物量影响

表格中的数据来自于相关文献，表中大针草和羊草为单位面积内所含有的植物种数。从最后的评分我们可以看出，随着放牧强度的增加，大针草和羊草的植物种树先增加后减少。无论是大针草还是羊草，群落种树均已轻中放牧策略最高，其次是无牧策略，最低是重牧策略。

2.2.2. 不同放牧强度对土壤湿度的影响

计算结果如下表2所示。

Table 2. Effects of different grazing intensities on soil moisture at different levels

表2. 不同放牧强度对不同层次的土壤湿度影响

从表中我们可以看出，0~10 cm土层含水量对放牧强度的反应较为敏感，随着放牧强度的变化呈现一定规律。第一次和第二次牧后测定结果表明，随着放牧强度的增加，不同深度的土壤含水量随之下降，第一次牧后以中牧评分最高，第二次以重牧评分最高，第三次牧后出现相反趋势，即随着放牧强度的增加，土壤含水量随之增加，但还是对照区的增加的幅度大，达到了评分最高 [4]。

由表中可以看出，土壤含水量由轻牧区的6.72%增加到重牧区的9.55%。主要是由于放牧导致地上生物量减少、植被盖度降低、水分蒸发和土壤紧实度增加，在雨后(尤其是大雨)，水分下渗很慢，滞留在土壤表层，放牧强度越大滞留越多，而该地区日照强烈，地表水分迅速蒸发，在一段时间后，放牧强度大的处理土壤含水量较低。第二次牧后，0~10 cm土层含水量，放牧处理间差异不显著，而第一次牧后和第三次牧后，则差异显著，表明随着干旱的加剧，放牧强度对土壤含水量的影响减弱。随着土层的加深，土壤含水量呈下降趋势。

3. 土壤湿度预测

土壤湿度是地球科学等多个领域的重要变量，同时也是连接陆地表面和大气之间循环过程的关键陆面变量，其时空变化对气象、气候和水文等方面至关重要，有助于提高对水、能源和碳循环的认知。

首先，把每年相同月份土壤湿度放在一起进行数据可视化，发现土壤湿度具有周期性的规律。所以本题采用的是基于时间序列优化的随机森林预测模型，在保持目前放牧策略不变的情况下，对不同深度土壤湿度进行预测。然后，我们对1~12月份的数据分别建立数学模型 [5]。以一月份为例，预测土壤湿度的过程分为三步：首先建立回归模型研究每年1月份湿度随土壤蒸发量与降水量变化的关系，其次用回归模型利用2012~2022年1月份的土壤蒸发量和降水变化的关系，最后根据2023年1月份的土壤蒸发量和降水量预测2023年1月的湿度，如图1和图2所示。

3.1. 随机森林预测模型

与单独的决策树模型相比，随机森林模型由于集成了多个决策树，其预测结果会更准确，它集成了决策树模型的众多优点，又规避了决策树模型容易过度拟合等缺点，泛化能力更强 [6]。本文用普通LSTM预测模型在每年1月份的土壤湿度训练过程进行对比。

Figure 1. Soil moisture statistics from January to June from 2012 to 2021 (January to March is 2012~2022)

图1. 2012年~2021年的1~6月的土壤湿度统计图(1~3月是2012~2022年)

Figure 2. Soil moisture statistics from July to December 2012~2021

图2. 2012~2021年7~12月的土壤湿度统计图

从图3~6我们可以看出随机森林预测模型在训练过程中准确度方面，相对于其他模型比较高。因此我们采用随机森林预测模型来预测2022年4月份~2023年12月份的土壤湿度。

Figure 3. Comparison of random forest and other forecasting models based on time series (soil moisture of 10 cm in January (kg/m²))

图3. 基于时间序列的随机森林和其他预测模型对比(1月份10 cm土壤湿度(kg/m²))

Figure 4. Comparison of random forest and other forecasting models based on time series (40 cm soil moisture in January (kg/m²))

图4. 基于时间序列的随机森林和其他预测模型对比(1月份40 cm土壤湿度(kg/m²))

Figure 5. Comparison of random forest and other forecasting models based on time series (100 cm soil moisture in January (kg/m²))

图5. 基于时间序列的随机森林和其他预测模型对比(1月份100 cm土壤湿度(kg/m²))

Figure 6. Comparison of random forest and other forecasting models based on time series (soil moisture of 200 cm in January (kg/m²))

图6. 基于时间序列的随机森林和其他预测模型对比(1月份200 cm土壤湿度(kg/m²))

3.2. 计算结果

由表3可见，土壤湿度受多个因素的影响，包括土壤湿度、土壤蒸发数据以及降水数据等，同时其可预测性通常源于其自身的持久性(滞后土壤湿度)或受其他外部强迫因素的影响。5月份及其以前是一个相对较湿润的时期，大多数年份的土壤湿度都处于中等湿度水平。进入6月份以后土壤含水量波动中迅速上升，总的来看10 cm土层的湿度基本表现出春冬季较低，而夏秋季稍高的特点。

Table 3. Prediction results of soil moisture at different soil levels

表3. 不同土壤层次的土壤湿度预测结果

4. 土壤中有机物的的预测

4.1. 预测模型

预测采用建立基于时间序列多层LSTM模型的回归预测。时间序列分析主要是根据已知历史数据对未来进行预测。该序列含有不同的成分，如趋势、季节性、周期性和随机性 [7]。对于一个具体的时间序列，他可能含有一种成分或者同时有几种成分，含有不同成分的时间序列所用的预测方法是不同的。预测步骤如下：首先确定时间序列所包含的成分，确定时间序列的类型，然后找出适合此类时间序列的预测方法，本题建立的是时间序列的回归预测模型，其次对可能的预测方法进行评估，已确定最佳预测方案，评价方法是找出预测值与实际值的差距，即预测误差 [8]。最优的预测方法就是预测误差达到最小的方法，最后利用最佳的预测方案进行预测，即时间序列的多层LSTM回归模型预测，如图7所示。

Figure 7. Structure diagram of LSTM

图7. LSTM的结构图

对于研究锡林郭勒草原土壤的化学性质，建立土壤湿度的自相关性和解释变量的数学模型，而统计方法采用线性拟合的方式预测土壤温湿度，其公式一般为：

$y_t={\beta }_0+{\beta }_1{x}_{1,t}+{\beta }_2{x}_{2,t}+\cdots +{\beta }_k{x}_{k,t}+{\epsilon }_t$ (11)

这里的每个自变量都必须是数字，而系数 ${\beta }_1,\cdots ,{\beta }_k$ 测量的是考虑了模型其他自变量后，每个自变量的影响。因此，这些系数从测量的也是自变量的边际效应。当我们使用线性回归模型时，我们对上面的多元线性回归公式中变量进行了一些假设 [9]：首先，我们假设模型是对现实的合理近似，即预测变量与自变量的关系满足该线性方程式，其次，我们对误差有以下假设 $\left({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_t\right)$

a. 他们的均值为0，否则预测的结果是有偏的；

b. 他们不会自相关，否则预测将变得效率低下，因为数据中有更多的信息可以被挖掘。

总结线性回归模型对数据的拟合程度方法是通过决定系数，或者说 $R^2$，这可计算观测值和预测值相关性的平方，其公式为：

$R^2=\frac{{{\displaystyle \sum }}^{\text{}}{\left(\hat{y}-\bar{y}\right)}^2}{{{\displaystyle \sum }}^{\text{}}{\left(y_t-\bar{y}\right)}^2}$ (12)

其中求和是贯穿所有观测值的求和，故它反映了回归模型所占的预测变量中变化的比例。回归方程的标准误差，另一种测量模型拟合数据效果的是用残差的标准差，通常称为残差的标准差，公式如下：

${\hat{\sigma }}_e=\sqrt{\frac{1}{T-k-1}}{\displaystyle {\sum }_{t=1}^T{e}_t^2}$ (13)

这里的k表示x变量得数量；注意到我们用T − k − 1去除，这是因为我们估计了k + 1个参数(截距及每个变量对应的系数)。标准误差与模型产生的平均误差大小有关；我们可将此误差与样本均值进行比较或者和y的标准偏差进行比较，从而对模型准确性有更进一步了解。

4.2. 数据可视化

为了便于观察锡林郭勒草原地检测样地的化学物质的情况，我们绘制出在不同的放牧强度条件下各个小区的2022年土壤同期有机碳、无机碳、全N、土壤C/N比等值随时间序列的波动图 [10]，如图8所示。

Figure 8. Maps of changes in soil chemistry in twelve regions (mg/kg)

图8. 十二个地区的土壤化学性质变化图(mg/kg)

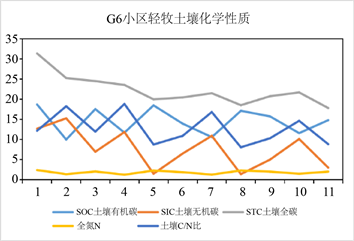
4.3. 预测结果分析

由表4我们可以了解到，随着放牧强度的增加，土壤的全氮含量上升，各处理间未达到显著差异。土壤无机碳含量随放牧强度的增加而降低。由于放牧强度对草原土壤化学物质的影响，不同元素有不同程度的影响，所以在考虑放牧时，应该以中等放牧强度为宜，使草地生态系统的物质循环与能量流动保持稳定。

Table 4. Twelve communities had organic matter content at different grazing intensities at the same time

表4. 十二个小区在不同的放牧强度同期有机物含量

5. 结语与建议

针对不同放牧策略对草原土壤板物理性质和植被生物量的评价模型，提出的熵权Topsis综合评价模型，具有较强的客观性，避免了数据的主观性，能够很好的刻画多个影响指标的综合影响力度。针对土壤湿度的预测，提出的基于时间序列的随机森林预测模型，预测精度较高，具有很好的鲁棒性。针对土壤有机物的评价和预测，采用综合评价加预测模型，综合评价采用的是加权重的Topsis法，对土壤中四种化学物质进行综合评价，预测模型采用的是基于时间序列的多层LSTM模型，在序列建模问题上具有一定的优势，具有长时记忆功能。在考虑土壤湿度的影响因素时，土壤湿度的影响因素是多种复杂因素共同的影响，在以后的研究过程，会更加深入的研究草原土壤湿度的影响因素，对模型进行充分的训练与测试，提高模型的鲁棒性和泛用性，进一步提高模型的精度。

NOTES

^*通讯作者。