1. 引言
首项为1，并通过连续增加算术级数中的公差得到的数字称为角数(或统称M角数)，由此得到
3角数：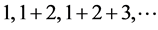
4角数：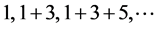
5角数：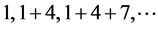
等等。
显然，4角数就是自然数平方的数列。我们知道，关于4角数数列
的Pythagorean方程
的离散性质是几何的起源，它的迷人魅力至今吸引着许多人研究和推广。
对于一般的M角数，Diophtantus用
表示m角数的第s项 [1] ，并用公式
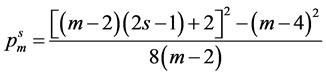
作为第s项m角数的几何定义1。因此，m角数的第s项公式也可以简化为如下形式
(1)
的递推法则是：
(2)
它属于一种比较简单的分层递推。
自从Lagrange证明了任意自然数都可以表示为m个m角数之和的Fermat命题之后，M角数的研究沉寂了很长时间。近十年来，M角数的研究主要集中在公式(2)的推广。文献 [2] 利用Brahmagupta引理 [3] 和Pellian方程用解析法求出了满足
3角数−5角数=1，3角数−7角数=1，3角数−8角数=1，3角数−10角数=1
3角数−12角数=1，5角数−6角数=1，5角数−7角数=1，5角数−8角数=1
条件的8个整数数列的Pellian表达式，又由表达式推出了8个数列项数的递推法则。
我们用符号
表示m角数的数列，用
表示m角数数列减n角数的差等于k的那些数所形成的数列，在这里
为正整数，且
。
由此，上面满足的条件可以简记为
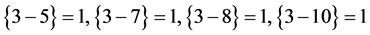
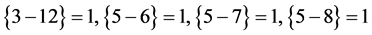
文献 [4] 研究了任意两种不同类m角数的上述情形，并给出了这些数列项数的递推法则。
更进一步，文献 [5] 求出了满足条件
的3角数递推法则为
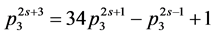
文献 [5] 还研究了满足
条件的一般数列表达式和n角数项数的递推法则。文献 [6] 研究了满足
和
条件的数列表达式以及3角数和n角数项的递推法则。
有了这些结果，我们很自然的想知道，条件k取负值时(或者距离4角数更远的那个角数)的递推法则是怎样的。当
时，就是求解满足条件
(或
)的序列。然而我们发现即这种最简单的情形，也找不到递推法则的一般求法。
文献 [7] 在这方面做了一些尝试。它指出：存在确定得法则，可以从3角数数列中找到同时等于5数、8角数、10角数和12角数的那些数。这方面的综述还可以参看文献 [1] 。
实际上，我们已经知道了
的一部分性质，在研究满足条件
的数列之前，我们还应该弄清楚它们的中间情形，即：满足条件
和
的数列的性质。
这是一项非常巨大的工作，我们可以只抽出
来研究，它表示的数列条件是两个m角数之差仍然属于m角数。通常情况下，我们可以只考虑这种数列为正整数数列。
显然，
表示直角三角形的通解数列。我们知道，当直角三角形的斜边长与一个直角边长为相邻的整数时，Pythagorean方程
的通解公式为
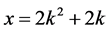
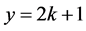
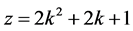
因此，斜边长与一个直角边长为相邻整数的Pythagorean方程为
(3)
它可以解释为：第
项自然数的平方(即4角数)与第
项自然数的平方之和等于第
项自然数的平方。当k取整数时，
。
本文把上述Pythagorean方程的通解公式推广到任意m角数，得到了下面的定理。
定理：第
项m角数与第
项m角数之和等于第
项m角数。式中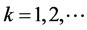
用M角数的符号也可以表示定理为
(4)
由M角数几何性质可以看出，公式(4)把直角三角形的Pythagorean方程推广到了凸多边形。
2. 定理的证明
证明：由m角数的第s项公式(1)我们得到
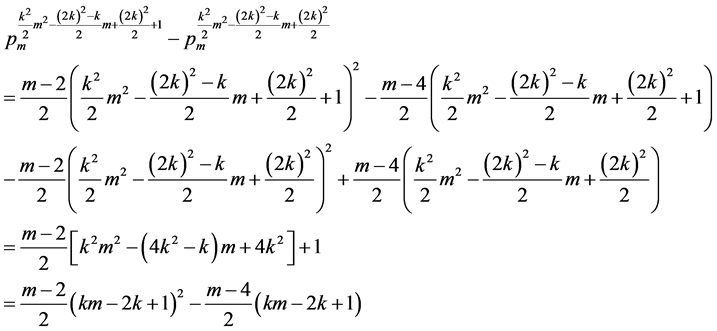
它恰等于第
项m角数
。□
虽然我们用代数的方法证明了定理。然而，讲明白这个定理中字符的一般意义并不是容易的事情。
3. 定理的代数意义
令：公式(4)可以表示为联立方程如下：
(5)
为了看清楚两种数组
的关系2，我们很容易计算得到下面的表1。
例如，查表1
得
。表示对应7角数的第214项和7角数的21项。又由7角数的计算公式得到第214项和第21项的7角数为114,169和1071。那么，由定理可以求得7角数的第215项等于114,169 + 1071 = 115,240。
相反的，我们知道，表1中的数组
也对应唯一的数组
。由上面的表1我们只能转换一部分数组
填写在下面的表2中，其它的数组
由方程组(5)确定。
由于代数方程表示的空间曲面是连续的，可以认为上述方程的有理数数组的解
连续且唯一。虽然用这种方法求解出方程组的精确解是繁琐的，但是求解的步骤是确定的。例如：当
时，我们通过求解4次方程得到解为
。
特别需要说明的是，定理中的
是表示差分常数一个量。即：从3角数开始，
的二次差分常数为自然数的平方
，
的一次差分常数为自然数
。例如
时
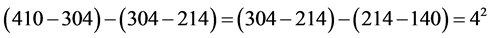
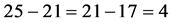
利用这个性质，我们由数组
可以递推的得到数组
，见下面的表2。这是一种简单的分层递推。表2中的规律性数字揭示的就是这种递推法则。
表1. 坐标m⊾k下，二元数组
表
表1中m = 2可以解释为2角数。不妨假定它的数值遵循相同的法则，可以由计算公式给出。
表2. 坐标X⊾Y下，二元数组
表
表2仅给出了k ≥ 1的数组，k < 1的数组属于虚数平面的性质，不在我们研究的范围内。
4. 推广和结论
我们可以扩充
为有理数，使得Pythagorean方程
的通解公式(3)表示任意直角三角形的有理数边长。显然，当
无重复的取遍所有的正的既约分数时，上式恰好无重复的取遍三边为互素整数的相似直角三角形的不同种类。
由定理的证明过程可以看出，这种方法同样适用于本文的定理。也就是说，表1和表2表示的两种平面m⊾k，X⊾Y存在着某种连续的性质 [8] ，这是一种不明显的推广。
表2给出的是
为自然数且
的逆定理3。对于4角数，定理和逆定理可以替换为满足本原方程
所有整数解的充分必要条件：
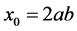
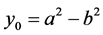
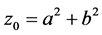
或者记为
(6)
公式中
是奇偶性相反并满足
的正整数，且
。
比较直角三角形公式
和
的整数解可以看出，
是这样一个有理数，它使得
和
分别表示两个相似直角三角形的两个直角边的边长。因此
是相似直角三角形的缩放系数，是角度的函数。显然，
也是角度的函数。
当然，也可以把数组
推广为任意有理数数组4，通过解方程组(5)并利用代数方程的连续性质得到逆定理的推广。
一般情况下，数组
是数组
为参数的三角函数数组，这两种有理数组及其映射关系属于Diophtantus方程(或离散数学及拓扑学)研究的范围。
综上所述，我们给出了把Pythagorean方程整数解的充分必要条件推广到任意M角数的一般方法。
5. 定理及逆定理在拓扑空间的应用
无论古典数学分支还是近代的数学分支，都以Pythagorean方程作为基本理论。下面，我们首先讨论Pythagorean方程的推广(即：本文的定理和逆定里)在拓扑学上的一个应用。
容易发现，表1第一列的数组可以直接转化为表2的第一列；表1中第一行的数组转换到表2时，都是表2所在行最后的一个组数，并且它们在同一条抛物线上。这些转换都是数组位置的映射，是拓扑。
由于表1和表2的有理数数组可以用自然数排序(可用自然数排序的集合称为偏序集)，即使我们扩充 为有理数(限定有理数的分子和分母不大于给定的定值，并逐步放松限定)，并逐步加密表1和表2以后，这种有理数组仍然可以用自然数排序。
在这种情况下，表1的数组表示的位置，映射到表2的数组表示的位置；以及两个数组位置连线的这种映射满足了拓扑空间的定义 [8] [9] ，因此表1到表2的映射构成了一个拓扑空间。
在上述拓扑空间中，表1上任意一个与轴线平行的直线都映射成表2上的一个二次曲线(仅第一列是一条直线，是
时的特例)，由公式(5)很容易得到这个性质。
上述位置和位置连线的映射也实际给出了一种拓扑椭圆，文献 [9] 仅证明了拓扑椭圆是存在的。
6. M角数的研究现状和展望
比较文献 [2] [4] [5] [6] [7] 和表2，容易发现，当 取适当的有理数时，就是文献 [2] [4] [5] [6] [7] 研究的内容，它们都属于求解二元二次Diophtantus方程。其表达式和递推公式只是表2中数组
的两个特殊性质。
另一方面，由表2的规律性数字和上面给出的拓扑空间可以直观的想象出，满足条件为
的数列在表2的“反面”，属于复数域，故不存在满足条件的项为自然数的递推公式。因此，满足条件为
的M角数关系式只能在不同
的角数中寻找。例如：我们计算很少几个有理数组
，就可以得到3角数和4角数的关系式(Plutarch定理 [1] )
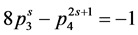
它是一个二次的代数关系式，但它不是满足条件
的递推公式。
众所周知，有一些数学问题用代数的方法解决很困难，另有一些数学问题用几何的方法解决很困难，还有一些数学问题仅用代数方法或仅用几何方法解决都是困难的。但很少有文献阐述出现这种现象的根源是什么？
本文的逆定理明确指出了产生这种困难的原因是高次方程多根的选择问题，由上面的讨论我们又可以看出，高次方程多根的选择问题可以扩充公式(4)中自然数
为有理数，并用拓扑的性质来替换。也就是说，拓扑几何把方程的求根和根的选择这两个步骤合并在了一起。
因此，涉及无穷概念(这里指偏序集)的连续问题，用几何的方法更直接；涉及无穷概念的离散问题，用代数的方法更直接。交替涉及连续和离散的问题，仅用代数方法或仅用几何方法解决都是困难的。
另一方面，高次方程多根的选择和公式(4)中自然数
扩充为有理数是等价的，都属于偏序集研究的范畴。由此可知，Diophtantus方程中未解决的离散问题(其中绝大部分都可以归类为分析学的问题)的解决方案，应该主要在偏序集理论中去寻找，直观的拓扑几何理论和许多代数理论很难解决这类问题，即使使用上奇异微积分理论也是如此。遗憾的是，偏序集理论远未达到完善的程度。
继续讨论上述的解决方案，不可避免的会涉及多个数学分支。不再这里赘述。
实际上，尽管本文给出了M角数的离散代数性质和拓扑几何性质，并对亏格为1的Diophtantus方程建立了代数和几何的联系。但M角数更多重要性质还远远没有被挖掘出来。
NOTES
1因为无法解释简化形式
的几何含义，因此不能用这个代数式定义M角数。
2仅当m = 4时，我们改用小写字母x，y表示X，Y，即：用x，y表示直角三角形的两个边长。
3用表1表示这个逆定理比用语言描述更清楚。逆定理的代数证明仅仅是描述用递推的方法求解二元二次方程组(5)的过程。但叙述极其繁琐，故略去。
4我们知道，解方程组(5)通常得到四组根。如选取实数组
，那么它的逆定理将不能确定那一组根
与
对应。因此它属于拓扑几何，不属于欧几里得几何。