Bernoulli机制下的带有负顾客、反馈和N策略的M/M/1休假排队

M/M/1 Queue with Negative Customers

摘要:

本文研究在Bernoulli机制下的带有负顾客、反馈和N策略的M/M/1休假排队系统，负顾客抵消队首正在接受服务的正顾客。在正规期，若系统中没有正顾客，服务台以概率α(0≤α ≤1)进入普通休假，或以概率β(β=1-α)进入工作休假。顾客在服务完成后以概率p(0≤p≤1)永远离开系统，或者以概率p(p=1-p)反馈到队尾继续等待服务。在休假期间，当顾客数大于等于N时，休假期结束。反之，则服务台继续休假。利用拟生灭过程和矩阵几何解的方法，得到了系统的稳态队长。最后，通过数值例子来说明一些参数对系统的影响。 In this paper, we study an M/M/1 queue with negative customers and feedback and N-policy under Bernoulli schedule. Negative customer removes positive customer being service at the head of the queue. During a normal period, when the system becomes empty, the server either begins an ordinary vacation with probability α(0≤α≤1) or takes a working vacation with probability β(β=1-α). When a positive customer completes his/her service, s/he may leave the system with probability p(0≤p≤1) or return to the back of the queue waiting for another service with probability p(p=1-p). When a vacation ends, if there are at least N customers in the system, the server switches to the normal working level. Otherwise, the server begins another vacation. Using quasi birth and death (QBD) process and matrix geometric solution method, we obtain the steady-state distribution for the queue length. Finally, some numerical examples are presented to show the effect of some parameters on the expected queue length.

1. 引言

在排队论中，休假排队一直是学者们研究的热点。Tian和Zhang曾研究过休假排队，详见参考文献 [1] 。在2002年，Servi和Finn [2] 首次提出半休假策略并研究了M/M/1/MV排队，即在休假期间服务员以低于正常期的服务率接待顾客，而不是对顾客完全停止服务，这类休假叫做工作休假(Working Vacation, WV)。这意味着，在休假期间仍保持一部分服务能力用于接待顾客，另一部分服务能力可进行缓冲调整或用于其他辅助任务。与经典的休假排队相比，工作休假可以更有效地保证系统的运行，达到减少系统损耗和减轻系统负载的双重作用，即在系统中，当主要工作相对较少时，可从事其他辅助工作。若是休假期间的服务率减小为零时，工作休假排队就变成了经典休假排队。因此，工作休假排队是经典休假排队的一种推广，工作休假策略允许服务员灵活的在高低速服务中转换，使得服务系统更加的接近实际，应用更广泛。对于工作休假排队模型，许多学者将它进行了推广。Wu和Takagi [3] 将M/M/1/MV排队模型扩展到M/G/1/MV排队模型，Baba [4] 利用矩阵几何解法研究了工作休假的GI/M/1排队模型，Krishnamoorthy 和Sreenivasan [5] [6] 分析了M/M/2的工作休假排队模型。

反馈机制也是排队论中研究的重要因素，尤其是Bernoulli反馈机制，被广泛应用于计算机分时操作系统和无线电通讯网络系统中。带有反馈的休假排队系统是经典休假排队系统服务机制发生变化的一种推广，即顾客到达系统后并不一定经过一次服务后就离开系统，可能经过多次，服务次数是由反馈机制决定的，详见参考文献 [7] [8] [9] 。刘名威和马永开 [10] 研究了Bernoulli反馈的N策略Geom/G/1排队系统的队长分布，刘红丹等 [11] 研究了有负顾客且Bernoulli反馈的M/M/C工作休假排队系统。

在本文中，我们通过Bernoulli控制策略将普通休假和工作休假结合在一起，即在正规期，若系统中无正顾客，服务员以概率 $\alpha$ 进入普通休假状态，或者以概率 $\beta$ 进入工作休假状态，其中 $0\le \alpha ,\beta \le 1$ 且 $\alpha +\beta =1$ 。在此情形下，我们还考虑了负顾客、反馈机制和N策略：负顾客抵消队首正在接受服务的正顾客；顾客在服务完成后以概率 $p\left(0\le p\le 1\right)$ 永远离开系统，或者以概率 $\bar{p}\left(\bar{p}=1-p\right)$ 反馈到队尾继续等待服务；在休假期间，当顾客数大于等于N时，休假期结束；反之，则服务台继续休假。

本节以下各节内容安排如下：第2节，我们给出了模型描述，并得到了QBD的正常返条件；第3节，利用最小非负解矩阵R，我们得到了不同状态下队长的平稳分布；第4节，通过数值例子来说明一些参数对系统队长的影响；第5节，结论。

2. 模型的描述

在M/M/1休假排队系统中引入负顾客、反馈机制和N策略，该排队模型具体描述如下：

1) 在系统中具有正、负两类顾客，这两类顾客的到达时间均服从泊松分布，参数分别为 $\lambda$ 和 $\epsilon$ 。

2) 负顾客本身不接受服务且带RCH抵消策略，即当负顾客到达时抵消队首正在接受服务的正顾客。若系统中没有正顾客，则负顾客没有影响并自动消失。

3) 在正规期，若系统中没有正顾客时，服务台以概率 $\alpha$ 进入一个随机长度为V的普通休假期，或者以概率 $\beta$ 进入一个随机长度为W的工作休假期。工作休假时间和普通休假时间分别服从参数为 $\theta$ 和 $\gamma$ 的指数分布。若休假结束时，系统中仍没有顾客，服务台则开始一个新的休假。在工作休假期间，服务台不停止服务，而是以较低的服务速率接待正顾客。在普通休假期间，服务台则停止服务。

4) 在正规期和工作休假期，服务台对正顾客的服务时间分别服从参数为 $\mu$ 和 $\eta$ 的指数分布，其中 $\mu \succ \eta$ 。

5) 按照先到先服务的原则，正顾客每服务完成一次后，以概率p永远离开系统，或者以概率 $\bar{p}\left(\bar{p}=1-p\right)$ 反馈到队尾等待再一次服务。

6) 系统中引入N策略休假原则：当普通休假和工作休假结束时，如果系统中的顾客数大于或等于N (N事先设定)，服务台立刻停止休假进入正规期。如果系统中的顾客数小于N，那么服务台的服务状态不变。

另外，假设正、负顾客到达时间间隔，正规忙期和工作休假期服务时间，普通休假时间，和工作休假时间均相互独立的，服务规则为先到先服务(FCFS)。

设 $Q\left(t\right)$ 表示t时刻系统中的正顾客数，

$J\left(t\right)=\{\begin{array}{l}0,系统在t时刻处于普通休假期\\ 1,系统在t时刻处于正规忙期\\ 2,系统在t时刻处于工作休假期\end{array}$

则 $\left\{Q\left(t\right),J\left(t\right)\right\}$ 是一个拟生灭过程，状态空间为

$\Omega =\left\{\left(k,j\right),k\ge 1,j=\mathrm{0.1.2}\right\}\cup \left\{\left(0,0\right)\right\}\cup \left\{\left(0,1\right)\right\}$

如果将状态按字典序排列拟生灭过程 $\left\{Q\left(t\right),J\left(t\right)\right\}$ 的最小生成元 $Q$ 可表示为下列分块矩阵形式

$Q=\begin{array}{c}0\\ 1\\ 2\\ ⋮\\ N-2\\ N-1\\ N\\ ⋮\end{array}\left[\begin{array}{ccccccccc}{A}_{00}& C_0& & & & & & & \\ B_0& A_0& C& & & & & & \\ & B& A_0& C& & & & & \\ & & \ddots & \ddots & \ddots & & & & \\ & & & B& A_0& C& & & \\ & & & & B& A_0& C& & \\ & & & & & B& A& C& \\ & & & & & & \ddots & \ddots & \ddots \end{array}\right]$ (1)

其中

$A_{00}=\left[\begin{array}{ccc}-\lambda & 0& 0\\ 0& 0& 0\\ 0& 0& -\lambda \end{array}\right]$ $C_0=\left[\begin{array}{ccc}\lambda & 0& 0\\ 0& 0& 0\\ 0& 0& \lambda \end{array}\right]$

$B_0=\left[\begin{array}{ccc}0& 0& 0\\ \alpha \left(p\mu +\epsilon \right)& 0& \beta \left(p\mu +\epsilon \right)\\ 0& 0& p\eta +\epsilon \end{array}\right]$ $A_0=\left[\begin{array}{ccc}-\lambda & 0& 0\\ 0& -\left(\lambda +p\mu +\epsilon \right)& 0\\ 0& 0& -\left(\lambda +p\eta +\epsilon \right)\end{array}\right]$

$C=\left[\begin{array}{ccc}\lambda & 0& 0\\ 0& \lambda & 0\\ 0& 0& \lambda \end{array}\right]$ $B=\left[\begin{array}{ccc}0& 0& 0\\ 0& p\mu +\epsilon & 0\\ 0& 0& p\eta +\epsilon \end{array}\right]$

$A=\left[\begin{array}{ccc}-\left(\lambda +\gamma \right)& \gamma & 0\\ 0& -\left(\lambda +p\mu +\epsilon \right)& 0\\ 0& \theta & -\left(\lambda +p\eta +\epsilon +\theta \right)\end{array}\right]$

在拟生灭模型的分析中，考虑矩阵二次方程

$R^{2}B+RA+C=0$ (2)

其中R为率阵，它是二次方程的最小非负解。

定理1 当 $\rho =\frac{\lambda }{p\mu +\epsilon }<1$ 时，方程(2)有最小非负解

$R=\left[\begin{array}{ccc}{r}_1& r_2& 0\\ 0& r_3& 0\\ 0& r_4& r_5\end{array}\right]$

其中， $r_1=\frac{\lambda }{\lambda +\gamma }$ ， $r_2=r_3=\frac{\lambda }{p\mu +\epsilon }$ ，

$r_4=\frac{\theta r_5}{\left(p\mu +\epsilon \right)\left(1-r_5\right)}$ ,

$r_5=\frac{\left(\lambda +p\eta +\epsilon +\theta \right)-\sqrt{{\left(\lambda +p\eta +\epsilon +\theta \right)}^2-4\lambda \left(p\eta +\epsilon \right)}}{2\left(p\eta +\epsilon \right)}$ .

证明：矩阵 $A,B,C$ 都是下三角矩阵，可以设 $R=\left[\begin{array}{cc}{R}_1& 0\\ R_2& R_3\end{array}\right]$ ，其中 $R_1,R_2,R_3$ 都是 $2\times 2$ 阶矩阵。将其代

入矩阵方程(2)，我们可得：

$\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]=R_1^2\left[\begin{array}{cc}0& 0\\ 0& p\mu +\epsilon \end{array}\right]+R_1\left[\begin{array}{cc}-\left(\lambda +\gamma \right)& \gamma \\ 0& -\left(\lambda +p\mu +\epsilon \right)\end{array}\right]+\left[\begin{array}{cc}\lambda & 0\\ 0& \lambda \end{array}\right]$

$\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]=\left(R_2{R}_1+R_3{R}_2\right)\left[\begin{array}{cc}0& 0\\ 0& p\mu +\epsilon \end{array}\right]+R_2\left[\begin{array}{cc}-\left(\lambda +\gamma \right)& \gamma \\ 0& -\left(\lambda +p\mu +\epsilon \right)\end{array}\right]+R_3\left[\begin{array}{cc}0& \theta \end{array}\right]$ ,

$\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]=R_3^2\left(p\eta +\epsilon \right)+R_3\left[\begin{array}{c}-\left(\lambda +p\eta +\epsilon +\theta \right)\end{array}\right]+\lambda$ .

整理得：

$\lambda -\left(\lambda +\gamma \right)r_1=0$

$\left(p\mu +\epsilon \right)\left(r_1{r}_2+r_2{r}_3\right)+\gamma r_1-\left(\lambda +p\mu +\epsilon \right)r_2=0$

$\left(p\mu +\epsilon \right)r_3^2-\left(\lambda +p\mu +\epsilon \right)r_3+\lambda =0$ (3)

$\left(p\mu +\epsilon \right)\left(r_3{r}_4+r_4{r}_5\right)+\gamma r_1-\left(\lambda +p\mu +\epsilon \right)r_4+\theta r_5=0$

$\left(p\eta +\epsilon \right)r_5^2-\left(\lambda +p\eta +\epsilon +\theta \right)r_5+\lambda =0$

解(3)中的第一个方程得。解(3)中的第三个方程得到一个根为 $\rho$ ，另一个根为1(舍去)。要使率阵R有最小非负解，需 $r_3=\rho =\frac{\lambda }{p\mu +\epsilon }$ 且 $\rho <1$ 。将 $r_1$ 和 $r_3$ 代入(3)中的第二个方程得 $r_2=\frac{\lambda }{p\mu +\epsilon }$ 。之后再解(3)中的第五个方程得到其中一个根为 $r_5$ ，另一个根大于1 (舍去)，即 $r_5=r=\frac{\left(\lambda +p\eta +\epsilon +\theta \right)-\sqrt{{\left(\lambda +p\eta +\epsilon +\theta \right)}^2-4\lambda \left(p\eta +\epsilon \right)}}{2\left(p\eta +\epsilon \right)}$ 。将 $r_3$ 和 $$ 代入(3)中的第四个方程可得 $r_4=\frac{\theta r_5}{\left(p\eta +\epsilon \right)\left(1-r_5\right)}$ 。容易验证满足：

$\left(\lambda +\theta \right)+\left(p\eta +\epsilon \right)\left(1-r\right)=p\eta +\epsilon +\frac{\theta }{1-r}=\frac{\lambda }{r}$ .

证毕。

定理2QBD过程 $\left\{Q\left(t\right),J\left(t\right),t\ge 0\right\}$ 正常返当且仅当 $\rho =\frac{\lambda }{p\mu +\epsilon }\prec 1$ 。

证明：首先，假设

$G=A+B+C=\left[\begin{array}{ccc}-\gamma & \gamma & 0\\ 0& 0& 0\\ 0& \theta & -\theta \end{array}\right]$

根据文献 [12] 定理2.5可得，若G不可约， $\pi$ 是G的平稳概率向量，即 $\pi G=0$ ， $\pi e=1$ ，则 $SP\left(R\right)\prec 1$ ，当且仅当 $\pi Be\succ \pi Ce$ ， $\pi =\left[\begin{array}{ccc}0& 1& 0\end{array}\right]$ 。

$\left(\begin{array}{ccc}0& 1& 0\end{array}\right)\left[\begin{array}{ccc}0& 0& 0\\ 0& p\mu +\epsilon & 0\\ 0& 0& p\eta +\epsilon \end{array}\right]\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]\succ \left(\begin{array}{cc}\begin{array}{cc}0& 1\end{array}& 0\end{array}\right)\left[\begin{array}{ccc}\lambda & 0& 0\\ 0& \lambda & 0\\ 0& 0& \lambda \end{array}\right]\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]$ .

通过计算求得正常返条件 $p\mu +\epsilon \succ \lambda$ 。

证毕。

3. 系统队长的性能指标

设 $\rho \prec 1$ ， $\left(Q,J\right)$ 表示过程 $\left\{Q\left(t\right),J\left(t\right)\right\}$ 的稳态极限，记它的分布为

, ${\pi }_k=\left({\pi }_{k0},{\pi }_{k1},{\pi }_{k2}\right),k\ge 1$ ,

${\pi }_{kj}=P\left\{Q=k,J=j\right\}=\underset{t\to \infty }{\lim }P\left\{Q\left(t\right)=k,J\left(t\right)=j\right\},\left(k,j\right)\in \Omega$

定理3当 $\rho =\frac{\lambda }{p\mu +\epsilon }\prec 1$ 时， $\left(Q,J\right)$ 的稳态分布是

当 $k\ge N-1$ 时，

${\pi }_{k0}={\pi }_{N-1，0}{r}_1^{k-N+1}$ ,

${\pi }_{k1}=\frac{r_2}{r_1-r_3}\left(r_1^{k-N+1}-r_3^{k-N+1}\right){\pi }_{N-1，0}+r_3^{k-N+1}{\pi }_{N-1,1}+\frac{r_4}{r_3-r_5}\left(r_3^{k-N+1}-r_5^{k-N+1}\right){\pi }_{N-1,2}$ , (4)

${\pi }_{k2}={\pi }_{N-1,2}{r}_5^{k-N+1}$ ;

当 $k\prec N-1$ 时，

${\pi }_{k0}=\frac{\alpha \left(p\mu +\epsilon \right)}{\lambda }{\pi }_{11}$ , (5)

${\pi }_{k1}=\frac{1-{\rho }^k}{1-\rho }{\pi }_{11}$ ，其中 $\rho =\frac{\lambda }{p\mu +\epsilon }$ ， (6)

${\pi }_{k2}={\pi }_{12}-\left({\pi }_{12}-{\pi }_{02}\right)\frac{1-q^k}{1-q}$ ，其中 $q=\frac{\lambda }{p\eta +\epsilon }$ ； (7)

${\pi }_{N-1,0}={\pi }_{N-2,0}$ , (8)

${\pi }_{N-1,1}=\frac{\lambda }{p\mu +\epsilon }{\pi }_{N-2,1}+\frac{\lambda }{p\mu +\epsilon }{\pi }_{N-1,0}+r_4{\pi }_{N-1,2}$ , (9)

${\pi }_{N-1,2}=\frac{\lambda }{\lambda +p\eta +\epsilon -\left(p\eta +\epsilon \right)r_5}{\pi }_{N-2,2}$ ; (10)

${\pi }_{02}=\frac{\beta \left(p\mu +\epsilon \right)}{\lambda -\left(p\eta +\epsilon \right)K}{\pi }_{11}$ , (11)

${\pi }_{12}=K{\pi }_{02}$ , (12)

其中 $K=\frac{q^{N-1}\left(q-r_5\right)-q\left(1-r_5\right)}{q^{N-1}\left(q-r_5\right)-\left(1-r_5\right)}$ ，并且 ${\pi }_{11}$ 可以通过正规化条件获得。

证明：利用矩阵几何解的方法(参考文献 [12] )，我们可以得到

${\pi }_k=\left({\pi }_{k0},{\pi }_{k1},{\pi }_{k2}\right)={\pi }_{N-1}{R}^{k-N+1}=\left({\pi }_{N-1,0},{\pi }_{N-1，1},{\pi }_{N-1,2}\right)R^{k-N+1}$ , $k\ge N-1$ . (13)

当 $k\ge N-1$ 时，

$R^{k-N+1}=\left[\begin{array}{ccc}{r}_1^{k-N+1}& \frac{r_2}{r_1-r_3}\left(r_1^{k-N+1}-r_3^{k-N+1}\right)& 0\\ 0& r_3^{k-N+1}& 0\\ 0& \frac{r_4}{r_3-r_5}\left(r_3^{k-N+1}-r_5^{k-N+1}\right)& r_5^{k-N+1}\end{array}\right]$ (14)

将 $R^{k-N+1}$ 代入上述方程中，我们可以得到(4)。同时， ${\pi }_0,{\pi }_1,\cdots ,{\pi }_{N-1}$ 满足

$\left({\pi }_0,{\pi }_1,\cdots ,{\pi }_{N-1}\right)B\left[R\right]=0$ ,(15)

其中，

$B\left[R\right]=\begin{array}{c}0\\ 1\\ 2\\ ⋮\\ N-2\\ N-1\end{array}\left[\begin{array}{cccccc}{A}_{00}& C_0& & & & \\ B_0& A_0& C& & & \\ & B& A_0& C& & \\ & & \ddots & \ddots & \ddots & \\ & & & B& A_0& C\\ & & & & B& A_0+RB\end{array}\right]$ (16)

$A_0+RB=\left[\begin{array}{ccc}-\lambda & \lambda & 0\\ 0& -\left(p\mu +\epsilon \right)& 0\\ 0& \frac{\theta r_5}{1-r_5}& -\left(\lambda +p\eta +\epsilon \right)+\left(p\eta +\epsilon \right)r_5\end{array}\right]$

因此，我们可以得到

$-\lambda {\pi }_{00}+\alpha \left(p\mu +\epsilon \right){\pi }_{11}=0$ , (17)

$\lambda {\pi }_{00}-\lambda {\pi }_{10}=0$ , (18)

$\lambda {\pi }_{k-1,0}-\lambda {\pi }_{k0}=0,\left(1\le k\le N-2\right)$ , (19)

$-\left(\lambda +p\mu +\epsilon \right){\pi }_{11}+\left(p\mu +\epsilon \right){\pi }_{21}=0$ , (20)

$\lambda {\pi }_{k-1,1}-\left(\lambda +p\mu +\epsilon \right){\pi }_{k1}+\left(p\mu +\epsilon \right){\pi }_{k+1,1}=0,\left(1\le k\le N-2\right)$ , (21)

$-\lambda {\pi }_{02}+\beta \left(p\mu +\epsilon \right){\pi }_{11}+\left(p\eta +\epsilon \right){\pi }_{12}=0$ , (22)

$\lambda {\pi }_{02}-\left(\lambda +p\eta +\epsilon \right){\pi }_{12}+\left(p\eta +\epsilon \right){\pi }_{22}=0$ , (23)

$\lambda {\pi }_{k-1,2}-\left(\lambda +p\eta +\epsilon \right){\pi }_{k2}+\left(p\eta +\epsilon \right){\pi }_{k+1,2}=0,\left(1\le k\le N-2\right)$ , (24)

$\lambda {\pi }_{N-2,0}-\lambda {\pi }_{N-1,0}=0$ , (25)

$\lambda {\pi }_{N-2,1}+\lambda {\pi }_{N-1,0}-\left(p\mu +\epsilon \right){\pi }_{N-1,1}+\frac{\theta r_5}{1-r_5}{\pi }_{N-1,2}=0$ , (26)

$\lambda {\pi }_{N-2,2}+\left[\left(p\eta +\epsilon \right)r_5-\left(\lambda +p\eta +\epsilon \right)\right]{\pi }_{N-1,2}=0$ . (27)

从(17)式到(19)式，我们通过计算可以得到(5)式。从(20)式到(21)式，我们通过计算得到(6)式。(7)式可以从(23)式到(24)式得到。将 $r_5$ 代入(26)式后，并与(25)式和(27)式一起计算，我们可以得到 ${\pi }_{N-1,0}$ ， ${\pi }_{N-1,2}$ 和 $$ 。通过(7)式、(24)式、(27)式，我们可以得到 ${\pi }_{02}$ 和 ${\pi }_{12}$ 。在(24)式中，让k等于 $N-2$ ，利用 ${\pi }_{N-3,2}$ ， ${\pi }_{N-2,2}$ 和 ${\pi }_{N-1,2}$ ，(12)式可以表示出来。将(12)式代入(22)式中，我们可以将 ${\pi }_{02}$ 用 ${\pi }_{11}$ 表示出来。最后，我们根据正规化条件

${\displaystyle \underset{j=0}{\overset{2}{\sum }}{\displaystyle \underset{k=0}{\overset{\infty }{\sum }}{\pi }_{kj}=1}}$ ,

我们可以求得 ${\pi }_{11}$ 。

证毕。

由定理3的结果可知，系统处于各个状态的概率为

$P\left\{I=0\right\}={\displaystyle \underset{k=0}{\overset{\infty }{\sum }}{\pi }_{k0}}={\displaystyle \underset{k=0}{\overset{N-2}{\sum }}{\pi }_{k0}}+{\displaystyle \underset{k=N-1}{\overset{\infty }{\sum }}{\pi }_{k0}}=\left(\frac{\alpha \left(p\mu +\epsilon \right)\left(N-1\right)}{\lambda }+\frac{\alpha \left(p\mu +\epsilon \right)}{\lambda \left(1-r_1\right)}\right){\pi }_{11}$ ,

$\begin{array}{c}P\left\{I=1\right\}={\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\pi }_{k1}}={\displaystyle \underset{k=1}{\overset{N-2}{\sum }}{\pi }_{k1}}+{\displaystyle \underset{k=N-1}{\overset{\infty }{\sum }}{\pi }_{k1}}\\ =\frac{\left(N-2\right)\left(1-\rho \right)-\rho +{\rho }^{N-2}}{{\left(1-\rho \right)}^2}{\pi }_{11}+\frac{r_2}{\left(1-r_2\right)\left(1-r_1\right)}{\pi }_{N-1,0}\\ +\frac{1}{1-r_3}{\pi }_{N-1,1}+\frac{r_4}{\left(1-r_3\right)\left(1-r_5\right)}{\pi }_{N-1,2}\end{array}$ ,

$\begin{array}{c}P\left\{I=2\right\}={\displaystyle \underset{k=0}{\overset{\infty }{\sum }}{\pi }_{k2}}={\displaystyle \underset{k=0}{\overset{N-2}{\sum }}{\pi }_{k2}}+{\displaystyle \underset{k=N-1}{\overset{\infty }{\sum }}{\pi }_{k2}}\\ ={\pi }_{02}+\left(N-2\right){\pi }_{12}+\frac{\left(N-2\right)\left(1-q\right)-q+q^{N-2}}{{\left(1-q\right)}^2}+\frac{1}{1-r_5}{\pi }_{N-1,2}\end{array}$ .

稳态下系统中的平均顾客数为

$\begin{array}{c}E\left[L\right]={\displaystyle \underset{k=0}{\overset{\infty }{\sum }}k\left({\pi }_{k0}+{\pi }_{k2}\right)}+{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}k{\pi }_{k1}}\\ ={\displaystyle \underset{k=0}{\overset{N-2}{\sum }}k\left({\pi }_{k0}+{\pi }_{k2}\right)}+{\displaystyle \underset{k=1}{\overset{N-2}{\sum }}k{\pi }_{k1}}+\frac{{\left(1-r_3\right)}^2+r_2\left(2-r_1-r_3\right)}{{\left(1-r_1\right)}^2{\left(1-r_3\right)}^2}{\pi }_{N-1,0}\\ +\frac{1}{{\left(1-r_3\right)}^2}{\pi }_{N-1,1}+\frac{{\left(1-r_5\right)}^2+r_4\left(2-r_5-r_3\right)}{{\left(1-r_5\right)}^2{\left(1-r_3\right)}^2}{\pi }_{N-1,2}\end{array}$ ,

则系统中顾客的等待时间为

$E\left[W\right]=\frac{E\left[L\right]}{\lambda }$ .

4. 数值分析

本文中，令 $\lambda =1.5$ ， $\eta =0.8$ ， $\gamma =0.6$ ， $N=2$ 以平均队长 $E\left(L\right)$ 作为研究对象，我们给出几个数值实例来演示普通休假状态概率 $\alpha$ 、正规期服务率 $\mu$ 对系统的影响。

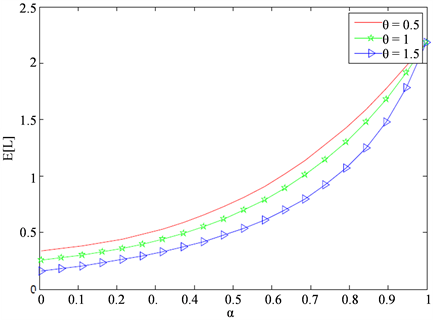
Figure 1. $E\left(L\right)$ with change of $\alpha$ (three different of $\theta$ )

图1. $E\left(L\right)$ 随 $\alpha$ 的变化趋势(三种不同的 $\theta$ )

令 $\mu =3$ ， $\epsilon =2$ ， $p=0.5$ 。图1描绘了普通休假状态概率 $\alpha$ 对平均队长 $E\left(L\right)$ 的影响。从图中，我们发现 $E\left(L\right)$ 随 $\alpha$ 的增大而增大。这是因为服务员在休假期内是不发生服务的，普通休假的概率越大，系统中的顾客数也会越多。而且 $\theta$ 越大，工作休假时间越短，系统中的顾客数越少。

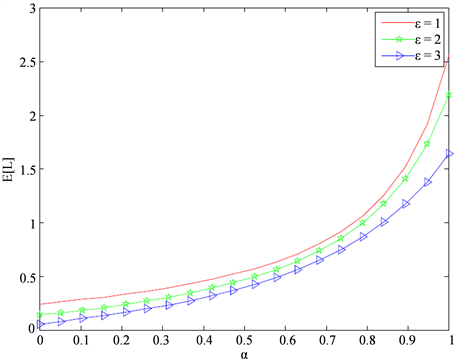
Figure 2. $E\left(L\right)$ with change of $\alpha$ (three different of $$ )

图2. $E\left(L\right)$ 随 $\alpha$ 的变化趋势(三种不同的 $\epsilon$ )

令 $\mu =3$ ， $\theta =0.4$ ， $p=0.5$ 。图2说明在三种不同的负顾客到达率 $\epsilon$ 下，平均队长 $E\left(L\right)$ 随普通休假状态概率 $\alpha$ 的增大而增大。由于服务员在休假期内是不发生服务的，因此普通休假的概率越大，系统中的顾客数也会越多。因为负顾客会抵消正在服务的顾客，所以负顾客到达率 $$ 越大，系统中的顾客数越少。

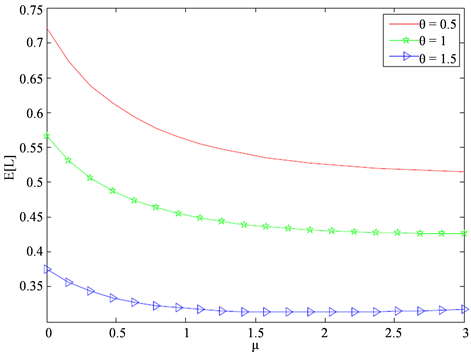
Figure 3. $E\left(L\right)$ with change of $\mu$ (three different of $\theta$ )

图3. $E\left(L\right)$ 随 $\mu$ 的变化趋势(三种不同的 $\theta$ )

令 $p=0.5$ ， $\alpha =0.3$ ， $\beta =0.7$ ， $\epsilon =2$ 。图3描绘了正规期服务率 $\mu$ 对平均队长 $E\left(L\right)$ 的影响。随着 $\mu$ 的增大，我们可以发现平均队长 $E\left(L\right)$ 在减少。在其他条件相同的情况下，平均队长 $E\left(L\right)$ 随 $\theta$ 的增大而减小。

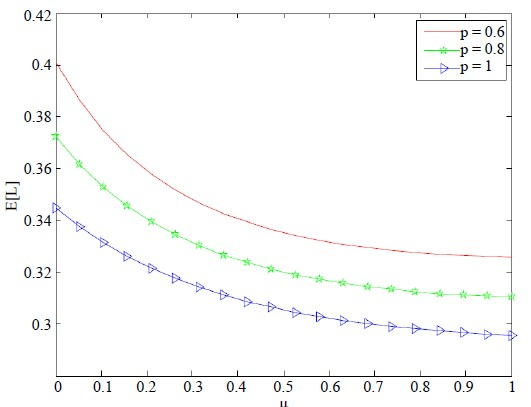
Figure 4. $E\left(L\right)$ with change of $\mu$ (three different of p)

图4. $E\left(L\right)$ 随 $\mu$ 的变化趋势(三种不同的p)

令 $\alpha =0.3$ ， $\beta =0.7$ ， $\epsilon =2$ ， $\theta =0.4$ 。图4描绘了正规期服务率 $\mu$ 对平均队长 $E\left(L\right)$ 的影响。随着 $\mu$ 的增大，我们可以发现平均队长 $E\left(L\right)$ 在减少。反馈概率p越大，系统中顾客在服务完成后离开系统的概率就越大，因此在其他条件相同的情况下，系统中的顾客数随着反馈概率p的增大而减少。

5. 结论

本文不同于普通的Bernoulli控制的M/M/1休假模型，而是在此基础上进一步研究了负顾客、反馈机制和N策略对模型的影响。通过对平均队长的分析，可以直观的看到各因素对系统的影响。特别地，当 $\epsilon =0$ ， $p=0$ 且 $N=1$ 时，该系统就退化为普通的Bernoulli控制的M/M/1休假模型。