1. 引言
本研究区位于鄂尔多斯盆地,鄂尔多斯盆地为一大型克拉通叠合盆地沉积了本溪组、太原组、山西组、下石盒子组、上石盒子组和石千峰组 [1],横跨伊盟隆起、伊陕斜坡和天环向斜三个构造单元 [2],油气勘探成果丰富 [3]。致密气约占我国天然气产量的30%,在我国能源结构中占据重要地位 [4]。目前,致密砂岩气已成为非常规天然气勘探的重点之一,是天然气增储上产的主体 [5] [6]。研究区存在的主要问题是存在严重的扩径现象,扩径现象对测井资料的影响不明确,已有钻井特别是探、评井的储层参数解释精度不高,含气性评价工作还达不到当前和未来勘探开发的要求,不能建立起全区性的含气性测井评价标准,部分井气层测井解释资料与射孔符合率偏低等问题。基于该研究现状,本文分析了研究区存在的扩径现象,将扩径程度进行了分类,并尝试分别使用人工神经网络法和多元回归法对研究区储层段非严重扩径部分和严重扩径部分的孔隙度建立了计算模型,以使孔隙度解释达到更高的精度从而为流体识别提供更精确的孔隙度参数。
2. 扩径对声波时差和密度测井曲线的影响分析
声波、密度以及中子测井是常规测井中用于计算孔隙度的最常用的曲线,称为三孔隙度曲线,但是三孔隙度测井曲线极易受到井眼条件的影响,导致测井曲线失真从而影响测井数据的准确性以及给后续的孔隙度参数预测造成极大的误差。现代常规测井使用的补偿声波以及补偿密度等能在一定程度上补偿井眼条件对测井数据带来的误差,但是研究区存在比较严重的扩径现象。将井径与钻头直径(21.6 cm)作差,定义为井眼扩径的大小。首先绘制扩径量(CAL-D)与声波时差和密度测井的交会图(图1和图2),可以看到,当扩径量(CAL-D) < 10 cm时,声波时差和密度没有明显的规律;当扩径量(CAL-D) ≥ 10 cm时,声波时差有沿图中斜线增大的趋势,密度有沿图中斜线减小的趋势,因此将CAL-D < 10 cm的部分划分为非严重扩径,CAL-D ≥ 10 cm的部分划分为严重扩径部分。
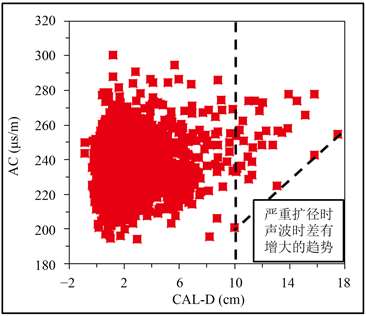
Figure 1. Cross plot of diameter expansion-acoustic time difference
图1. 扩径量–声波时差交会图
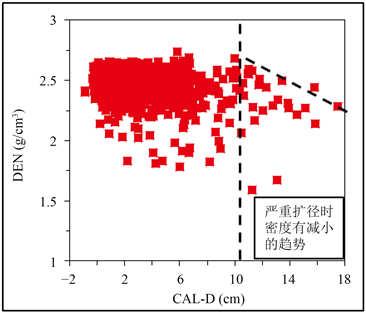
Figure 2. Cross plot of diameter expansion-acoustic compensation density
图2. 扩径量–补偿密度交会图
图3和图4为研究区内两口单井砂岩段单井柱状图,红框内为严重扩径部分,其余部分为非严重扩径部分,可以看到,非严重扩径部分声波和密度由于测井仪器的补偿作用,测井值基本不受扩径影响或受影响极其微弱;而严重扩径部分密度极易受到影响出现跳动而使测井值严重失真,声波则仍然能受到较好的补偿作用而使测井值不受影响或者影响极其微弱。
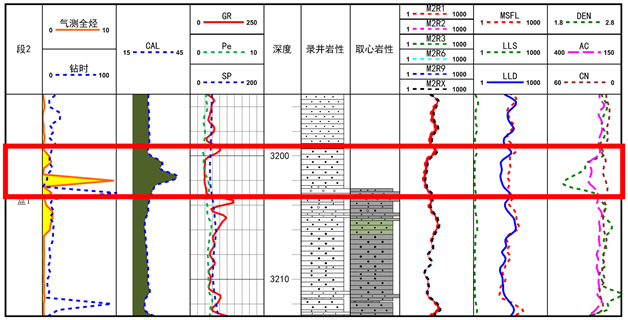
Figure 3. Single well histogram of Well H1
图3. H1井单井柱状图
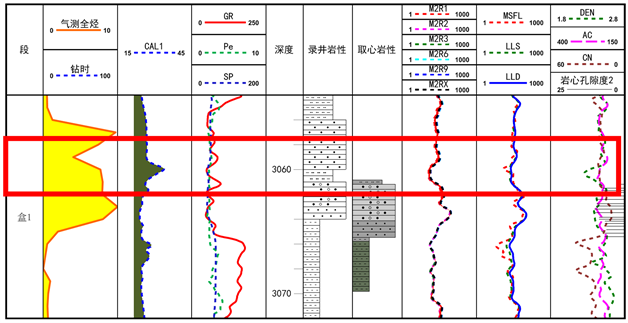
Figure 4. Single well histogram of Well H1
图4. H1井单井柱状图
通过以上分析,发现非严重扩径的情况下,声波和密度均不受扩径影响或者受影响较微弱,因此在非严重扩径的情况下,声波和密度仍然能作为计算孔隙度的输入曲线;而严重扩径情况下,声波仍然能作为计算孔隙度的曲线,而密度由于严重失真无法采用,因此将研究区的孔隙度分为非严重扩径和严重扩径两种情况进行校正。
3. 非严重扩径储层段神经网络孔隙度预测
研究区原先采用的是声波时差拟合计算的孔隙度,最后得到的孔隙度解释精度低,无法满足后续研究要求,因此本文采用非线性的人工神经网络法对孔隙度进行校正,以期达到更高的储层孔隙度解释精度。
3.1. BP神经网络原理
除BP神经网络是一种采用误差反向传播算法的多层前馈人工神经网络,具有任意复杂的模式分类能力和优良的多维函数映射能力,解决了简单感知器不能解决的异或(Exclusive OR, XOR)和一些其他问题 [7]。BP神经网络的结构如图5,由输入层、隐层和输出层三部分组成,其中,可以有多个隐层。
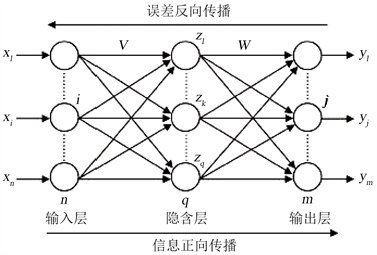
Figure 5. Schematic diagram of BP neural network model structure
图5. BP神经网络模型结构示意图
3.2. 相关性分析及输入曲线的选择
除建立BP神经网络孔隙度预测模型之前,输入样本的挑选至关重要。因此需要进行测井曲线标准化、岩心归位和深度校正等一系列操作,从而使得岩心物性参数和电性曲线的对应性更好,从而使得电性测井资料更能准确的反映储层孔隙度。与常规的线性多元回归法计算孔隙度类似,与孔隙度相关性越好的测井曲线越对孔隙度预测有利。同时,BP神经网络对信息具有一定的冗余性,因此,除了选择声波和密度测井曲线外,还可增加几条测井曲线,以尽可能的挖掘曲线信息,从而使预测的孔隙度更加准确。
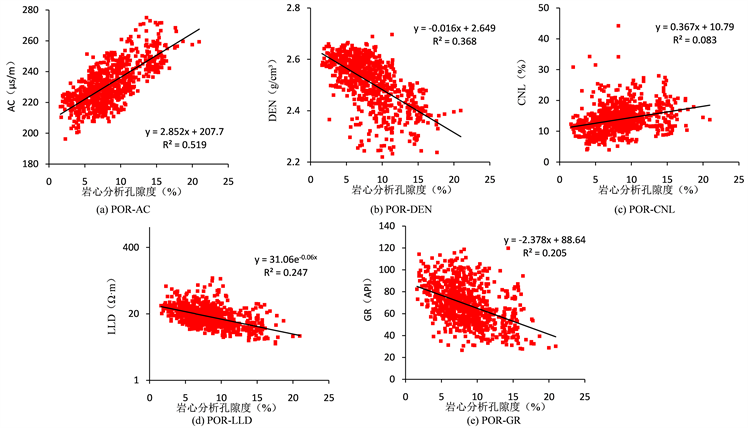
Figure 6. Cross plot of core porosity and each input curve
图6. 岩心孔隙度与各输入曲线交会图
图6为岩心孔隙度与各测井曲线的相关性图。岩心分析孔隙度与声波和密度的相关性最好,与电阻率和自然伽马的相关性其次,与补偿中子的相关性最差。最终,选择AC、DEN、CNL、LLD、GR作为BP神经网络模型的输入曲线。
3.3. BP神经网络模型的建立及学习效果评价
BP神经网络的产生归功于BP算法的获得,该算法由Rumelhart等在1986年提出,是一种监督式的学习算法主要由信息的正向传播与误差的反向传播两部分组成 [8] [9] [10] [11]。在选择AC、DEN、CNL、LLD、GR作为BP神经网络模型的输入曲线的基础上开始建立神经网络模型,即输入层神经元数目为5;隐层神经元初始可选为输入层神经元数的1~1.5倍,并由网络结构优化法在学习过程中自动地确定最佳隐层单元数 [12];输出层神经元数目为1,即为要预测的孔隙度。最终确定的模型结构如图7,采用输入神经元数目为5,隐层为1层,隐层神经元数目为9,输出神经元为1 (即孔隙度)的结构。
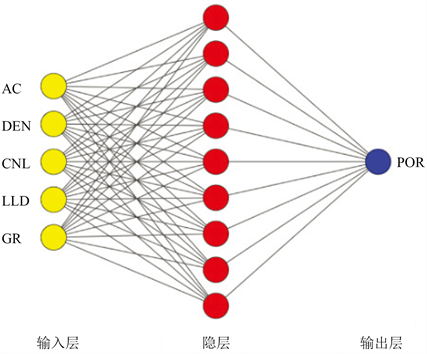
Figure 7. Neural network model structure of non-serious enlarged reservoir
图7. 非严重扩径储层神经网络模型结构
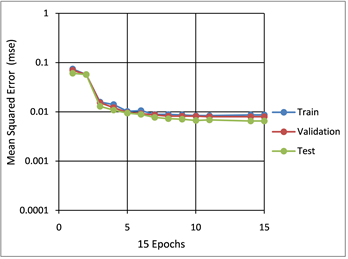
根据确定的神经网络结构,挑选合适的岩心样本,剔除异常点并将数据归一化后导入MATLAB软件使用神经网络模块建立神经网络模型。最终总共挑选了842个样本,777个样本用于神经网络训练和建模,64个样本用于对模型进行检验,设置最大迭代步数为1500,给定误差精度为0.001,模型的迭代9步后停止(图8(a)),最终训练精度为0.85 (图8(b))。学习精度达到了0.85,效果较好。
3.4. 模型的检验与误差分析
将预留的64个样本的测井值进行归一化后输入建立好的神经网络模型,使用模型计算预留样本的孔隙度,并绘制计算孔隙度与岩心孔隙度的交会图如图9。预测的孔隙度与岩心分析孔隙度的拟合精度达到了0.88,满足测井计算的需求。
计算所有842个样本神经网络计算孔隙度与岩心分析孔隙度的绝对差值,孔隙度绝对误差分布在0%~5.849%之间,平均绝对误差为1.357%,误差小,完全满足孔隙度计算误差和精度要求。表1为研究区部分岩心样本神经网络孔隙度与岩心分析孔隙度的误差表。
 (a)
(a) 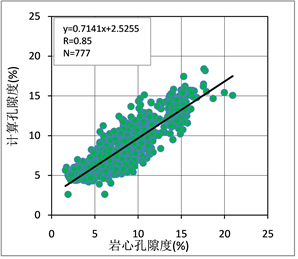 (b)
(b)
Figure 8. Training diagram of neural network porosity model for non-severe enlarged reservoir. (a) Iterative diagram of porosity model training for non-serious enlarged reservoir. (b) Correlation Analysis of Learning Accuracy of Porosity Model in Non-serious Enlarged Reservoir
图8. 非严重扩径储层神经网络孔隙度模型训练图。(a) 非严重扩径储层孔隙度模型训练迭代图(b) 非严重扩径储层孔隙度模型学习精度相关性分析
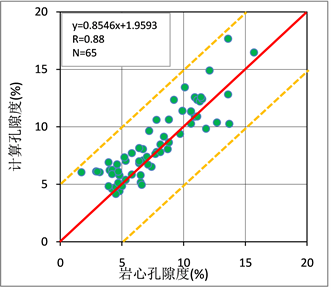
Figure 9. Porosity prediction accuracy chart of neural network in non-severe enlarged reservoir
图9. 非严重扩径储层神经网络孔隙度预测精度图


Table 1. Error table of porosity calculated by neural network (partial)
表1. 神经网络计算孔隙度误差表(部分)
3.5. 曲线重叠法效果评价
运用建立的神经网络模型对研究区单井非严重扩径砂岩段的孔隙度进行计算,并导入单井中对比计算结果与岩心结果的叠合效果。图10为研究区内单井储层段孔隙度计算成果图,最后一道的蓝色曲线为神经网络计算的孔隙度结果曲线,与岩心分析孔隙(黑色杆状离散曲线)的叠合效果好,计算精度高,能为后续的研究提供更准确的孔隙度参数。
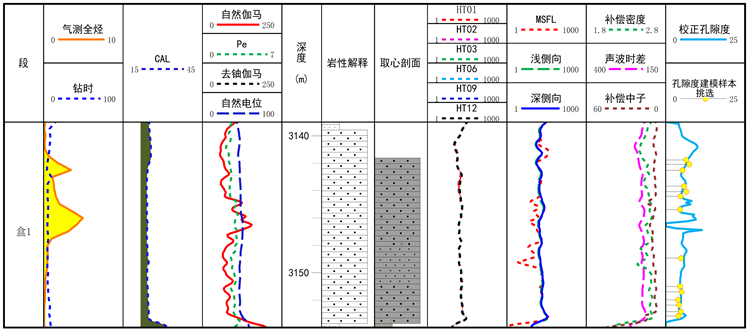
Figure 10. Porosity parameter interpretation results of well H5
图10. H5井孔隙度参数解释成果图
4. 严重扩径段孔隙度预测
4.1. 多元回归模型的建立
利用测井资料及其它已知的物性特征来预测未取芯井的孔隙度是油(气)藏描述的关键之一 [13] [14] [15]。在严重扩径条件下密度测井曲线受影响失真严重,因此不能使用密度曲线作为计算孔隙度的自变量。由于严重扩径段在研究区储层段占比少,严重扩径岩心样本极少,且声波时差等其他曲线受扩径影响微弱,因此选择声波时差和深侧向电阻率曲线用已经筛选好的岩心样本拟合多元回归公式即可满足对少量严重扩径储层段的孔隙度计算需求。
将准备好的样本集数据导入SPSS软件,选择多元回归模块,自变量选择声波时差曲线和深侧向电阻率的对数,因变量选择孔隙度,然后进行回归拟合。图11为拟合的结果图,拟合精度R = 0.73,最终得到的孔隙度计算公式为:
(1)

Figure 11. Fitting result of multivariate regression porosity calculation model for severely enlarged reservoir section
图11. 严重扩径储层段多元回归孔隙度计算模型拟合结果
4.2. 严重扩径段孔隙度预测
运用拟合的多元回归公式单独对研究区内的严重扩径段的孔隙度计算,并将结果导入单井图。图12为研究区单井严重扩径层段孔隙度预测成果图,可以看到图中最后一道预测的孔隙度(蓝色曲线)与岩心分析孔隙度(黑色杆状离散曲线)同样具有较好的重叠性。说明模型效果好,计算的孔隙度参数同样能满足后续研究的需求。
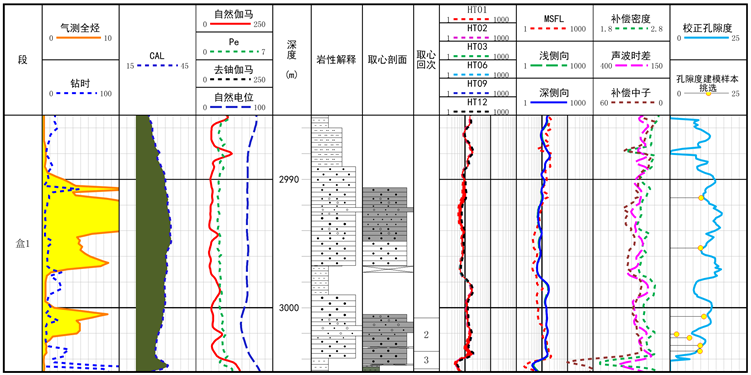
Figure 12. Porosity parameter interpretation results of well H8
图12. H8井孔隙度参数解释成果图
5. 孔隙度校正效果评价
在严重扩径和非严重扩径条件下,分别使用了不同的方法来校正孔隙度,通常来说,神经网络法使用的测井信息更多,且为非线性模型,能比多元回归达到更好的效果,单由于在严重扩径条件下测井曲线失真严重,因此无法使用神经网络法,只能使用多元回归法来计算,两种条件下使用的方法差异具体对比如表2。

Table 2. Difference of porosity correction methods under severe and non-severe expanding conditions
表2. 严重扩径和非严重扩径条件下孔隙度校正方法差异
将重新计算后的孔隙度与先前仅使用声波时差拟合计算结果作对比,发现新计算的孔隙度效果要远好于先前计算的孔隙度。图13为H7井3009~3044 m的孔隙度校正成果图,最后一道蓝色曲线为重新计算的校正后的孔隙度,橙色曲线为先前使用声波时差拟合公式计算的孔隙度,可以看到校正后的孔隙度与岩心分析孔隙度的叠合度要明显好于先前计算的孔隙度。如3016~3020 m处、3023~3027 m以及3032~3034 m处,先前计算的孔隙度要明显高于岩心分析计算的孔隙度;而使用新方法计算的校正后的孔隙度与岩心分析孔隙度的叠合程度较好。说明将研究区储层分为非严重扩径部分和严重扩径部分,并分别使用神经网络法和多元回归法计算的孔隙度具有更高的预测精度,能为后续的流体识别等工作提供更为准确的孔隙度参数。
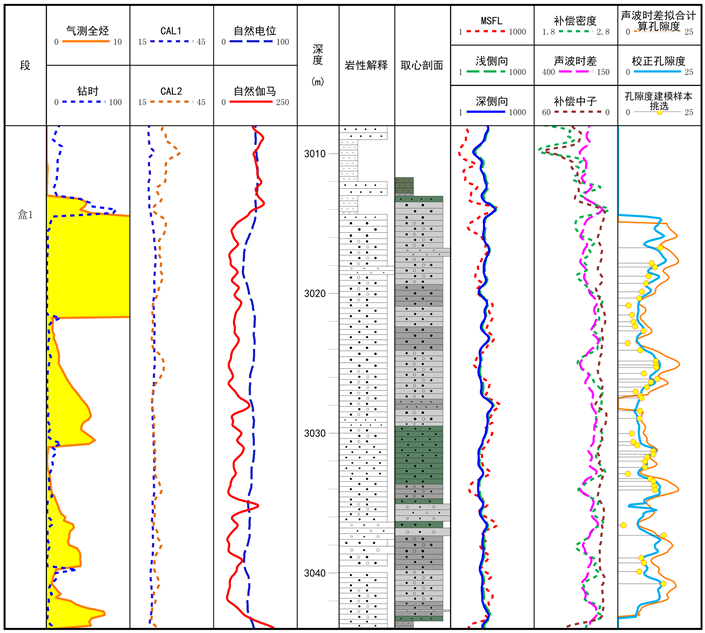
Figure 13. Porosity parameter interpretation results of well H7
图13. H7井孔隙度参数解释成果图
6. 结论
1) 研究区有存在比较严重的扩径现象,将扩径程度分为非严重扩径(CAL-D < 10 cm)和严重扩径(CAL-D ≥ 10 cm)两个部分,非严重扩径程度下声波时差和密度测井均不受扩径影响或者受扩径影响小;严重扩径情况下声波受影响微弱,密度受影响严重而导致曲线失真。
2) 针对研究区的扩径现象,在非严重扩径条件下建立了神经网络孔隙度计算模型;在严重扩径条件下使用多元回归法建立了孔隙度计算模型;并用建立好的计算模型计算孔隙度,计算结果与先前的模型相比,岩心分析孔隙度与计算孔隙度的重叠性更好,误差更低,精度更高。
3) 使用本文的方法在杭锦旗地区盒一段的单井孔隙度解释中均取得的较好的成果,效果好于先前使用声波时差计算的孔隙度,能为后续的研究提供更为准确的孔隙度参数。