具有不完全信息的M/M/1延迟工作休假系统中的社会最优策略

Social Optimal Strategy in M/M/1 Delayed Working Vacations with Incomplete Information

摘要: 本文将延迟假期和工作休假相结合，研究了具有不完全信息精度的M/M/1延迟工作休假系统的社会最优策略和定价策略。本文给予普通休假模型一个延迟时间，即当系统为空时，服务器进入延迟期，如果顾客在这段时间内到达，则服务器立即转入工作期以正常速率为顾客服务。否则，延迟时间过后，服务器会马上进入休假模式，开始进入缓慢工作的状态，如果服务器在工作休假期为一个顾客服务完成后，系统内仍然有剩余没有接受服务的顾客，那么排队系统将会结束慢速工作的休假状态，转而开始正常工作；若服务的顾客是最后一位顾客，且服务完成后再没有顾客进入系统，服务器则继续保持休假模式，直到休假时间结束或又有新顾客进入系统等待服务。本文考虑两类不完全信息精度情形：1) 几乎不可见情形：顾客在到达的瞬间只能观察到服务器的状态，不知道在场的顾客数量；2) 完全不可见情形：顾客既在到达的瞬间既不能观察到服务器的状态，也不知道在场的顾客数量。本文在这两种情形下利用矩阵几何解得到了平稳概率分布和平均队列长度。根据系统信息精度和顾客的预期收益及等待成本的线性收益–成本结构，确定了社会收益函数，得到了社会最优策略。最后，通过具体例子比较说明主要参数对社会最优策略的影响。

Abstract: This paper studies the social optimal strategy and pricing strategy under the background of M/M/1 delayed working vacations with incomplete information accuracy. This paper gives a delay time to the ordinary leave model, that is, when the system is empty, the server will stay in the system for a period of time. If the customer arrives during this period of time, the server enters the delay period. Otherwise, the server will turn on the working leave mode. If there are customers waiting in the system at the moment of service completion in the working leave period, the system will end the working leave and enter the normal working state. Otherwise, the server will continue to leave until a customer appears or the leave ends. This paper considers two kinds of incomplete information accuracy cases: 1) Almost invisible situation: the customer can only observe the state of the server at the moment of arrival and does not know the number of customers present; 2) Completely invisible situation: customers can neither observe the sta-tus of the server nor know the number of customers present at the moment of arrival. In these two cases, we obtain the stationary probability distribution and the mean queue length by using the matrix-geometric solution method. Based on the linear reward-cost structure of system information accuracy, customer expected benefits, and waiting costs, the social welfare function is determined, and the social optimal strategy is obtained. Finally, numerical examples are given to illustrate the impact of main parameters on social optimal strategy.

1. 引言

随着社会的不断进步，人们的生活水平也在不断提高，生活中因排队等待的现象屡见不鲜。在排队的时候会发生很多复杂的难以预料的情况，所以排队论有相当的研究深度，研究模型也比较复杂，排队论是一个新兴方向，有很大的研究意义。在过去的几十年里，越来越多的学者热衷于从博弈论和经济学角度研究排队系统，这项研究可以追溯到Naor [1] 学者的开创性论文，他分析了可见情形下M/M/1排队系统中顾客决策与服务器定价策略问题，在此前提下顾客会自己选择加入系统或离开，顾客的最优策略即确定阈值，当队伍中的人数小于该值，则新到的顾客选择加入，反之选择离开。每一位选择加入的顾客都会被收取等额费用，这种策略能够最大化获得社会收益，但无法保证服务器可以获得最大的利润。Edelson等 [2] 补充了Naor [1] 的不可见情形，并发现在不可见情形下，顾客在计算等待时间的期望值时，会使用到排队系统的其他的参数，最后再结合服务器的定价是否符合顾客预期收益的前提下做出相应决策。在这种不可见情形下，顾客并不是只能采取纯策略，也有可能采取混合策略。该文献还证明了存在着由顾客收益决定的唯一的均衡策略。从那时起，许多学者以此为基础，开始研究包含不同特征的各种排队系统的均衡策略型问题。

Economou等 [3] 首先考虑了完全可见和几乎可见情形下带有故障和维修的马尔可夫单服务器队列的平衡阈值策略，推导出了不同信息水平下的顾客均衡策略，并分析了这些策略下的社会收益。Guo和Hassin [4] 研究了具有N策略的M/M/1队列中的社会收益和顾客策略行为，其中包含加入或止步行为。Liu [5] 等研究了可见情形下单休假M/M/1排队系统，该模型在系统为空时，服务器只能进行一次休假，并推导出了在均衡状态下的阈值策略，并在相应的策略下分析了平稳系统的行为。Zhang [6] 等和Sun和Li [7] 研究了多重工作假期的M/M/1排队系统顾客的均衡策略，还计算出了社会最优加入策略和社会最优收益。然后，Tian [8] 等研究了三种不同信息(可见情形、几乎可见情形、完全不可见情形)下具有多个工作假期和假期中断的M/M/1队列的顾客均衡策略和社会最优策略。Li等 [9] 讨论了具有工作休假和休假中断的M/M/1排队模型，根据系统动态变化，其服务速率在低值和高值之间切换，给出了顾客均衡策略和系统在这些策略下的平衡行为。关于带假期的战略排队系统的全面而优秀的研究，读者可参考Hassin著作的第10章 [10] 。在不同排队系统中，探究顾客均衡策略与社会最优策略问题离不开对该系统的性能分析，众多学者根据系统的不同特点采用不同的方法。Servi [11] 受多个波长的WDM光接入网络的启发，首次在研究M/M/1排队系统时加入了多重工作休假机制，并以系统稳态为前提进行性能分析，得到平均队伍长度的母函数与平均等待时间的Laplace变换。后来，Liu等 [12] 用拟生灭过程与矩阵几何解的方法得到了M/M/1排队系统处于稳态下的各项指标的显式解及其随机分解结构。Xu等 [13] 利用拟生灭过程和矩阵几何解方法通过求解工作休假M/M/1排队系统，得到稳态排队系统中顾客数量的概率分布，同时得到排队系统中各种稳态信息的随机分解。张和王 [14] 对正规忙期和工作休假期服务的顾客数服从不同分布的M/M/1排队模型进行分析，用GI/M/1型马尔可夫过程建模，求解除系统稳态的分布及队长的随机分解结构。Baba [15] 研究了到达过程为一般分布的GI/M/1工作休假模型，求解了顾客数的稳态分布与顾客平均逗留时间。

本文将延迟假期和工作休假相结合从系统管理者与服务器的角度研究了延迟工作休假M/M/1系统背景下的社会最优策略，补充了赵 [16] 仅从顾客角度的研究；且不同于Tian [17] 所研究的延迟休假下的社会最优策略，本文将延迟假期与工作休假相结合，研究其社会最优策略。本文的前提为顾客在到达排队系统时并不知道系统中所有顾客的数量，并且顾客只能选择立即加入排队系统或者离开系统。将顾客到达时对服务器的了解情况分为以下两种：1) 几乎不可见情形：在进入排队系统前顾客并不清楚服务器的状态，服务器的状态只能在顾客在到达排队系统的那个时刻得知。2) 完全不可见情形：顾客始终无法知道服务器的状态。本文分别探究了两种情形下对应的社会效益最优策略。本文分为如下部分：第2节对几乎不可见情形与完全不可见情形下的社会最优策略进行了相关研究，并研究了在最优策略下的利润最大化问题。在第3节中，本文通过对不同数值例子比较说明了主要参数对社会最优策略的影响。最后，在第4节总结了本文的研究成果。

2. 模型介绍

考虑延迟工作休假M/M/1系统。顾客的到达数服从参数为 $\lambda$ 的泊松分布，工作状态下的顾客服务时间服从参数为 $\mu$ 的负指数分布，工作休假状态下的顾客服务时间服从参数为 $\eta$ 的负指数分布，延迟时间服从参数为 $\xi$ 的负指数分布，工作休假的时间服从参数为 $\theta$ 的负指数分布。本文假设顾客的到达间隔，服务器的服务时间和服务器处于休假状态下的服务时间三个变量之相互独立。服务器符合先进先出原则。用 $N\left(t\right)$ 表示系统在时间t的顾客数量，令

$J\left(t\right)=\{\begin{array}{l}0,服务器在t时刻处于休假期,\\ 1,服务器在t时刻处于忙期或有延迟.\end{array}$ (1)

则 $\left\{\left(N\left(t\right),J\left(t\right)\right),t>0\right\}$ 是一个状态空间为 $\Omega =\left\{\left(n,i\right)|n\ge 0,i=0,1\right\}$ 的过程。

本文假设顾客个体之间是相互独立的，不会受彼此影响。服务器为一个顾客服务完成后，该顾客得到R个单位的收益，并且顾客的每时间单位等待成本为C。由此，顾客的收益包括接受服务的收益减去基于线性成本结构的等待成本。顾客是风险中立的，即单位时间的期望收益等价于单位时间内确定的收益，并最大化他们的预期净收益。最后，我们假设没有拒绝顾客的重试，也没有拒绝等待顾客。

2.1. 几乎不可见情形

顾客可使用四种纯策略，即在状态 $i\left(i=0,1\right)$ 时加入队列或不加入队列。纯策略或混合策略的加入概率可以用 $q_i\left(0\le q_i\le 1\right)$ 表示，即服务器处于状态 $i\left(i=0,1\right)$ 时加入的概率，则到达顾客的有效到达率为 $\lambda q_i$ ，转换图如图1。

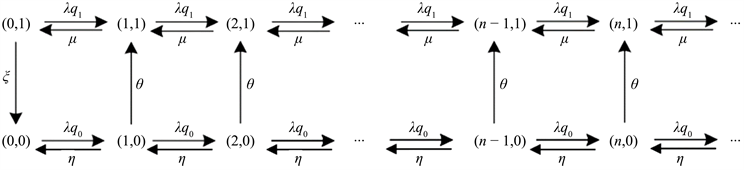
Figure 1. Transition rate diagram in almost invisible situation

图1. 几乎不可见情形下的转换速率图

转移概率矩阵Q可以写成下列分块三对角形式

$Q=\left(\begin{array}{cccc}{A}_0& C& & \begin{array}{ccc}& & \end{array}\\ B& A& C& \begin{array}{ccc}& & \end{array}\\ & B& A& \begin{array}{ccc}C& & \end{array}\\ \begin{array}{c}\\ \end{array}& \begin{array}{c}\\ \end{array}& \begin{array}{c}B\\ \end{array}& \begin{array}{ccc}\begin{array}{c}A\\ \ddots \end{array}& \begin{array}{c}C\\ \ddots \end{array}& \begin{array}{c}\\ \ddots \end{array}\end{array}\end{array}\right)$ , (2)

其中

$\begin{array}{l}{A}_0=\left(\begin{array}{cc}-\lambda q_0& 0\\ \xi & -\left(\lambda q_1+\xi \right)\end{array}\right),B=\left(\begin{array}{cc}\eta & 0\\ 0& \mu \end{array}\right),\\ A=\left(\begin{array}{cc}-\left(\lambda q_0+\theta \right)& \theta \\ 0& -\left(\lambda q_1+\mu \right)\end{array}\right),C=\left(\begin{array}{cc}\lambda q_0& \theta \\ 0& \lambda q_1\end{array}\right).\end{array}$ (3)

这个结构表明 $\left\{\left(N\left(t\right),J\left(t\right)\right),t>0\right\}$ 是一个拟生灭过程，Neuts [18] 经过研究得到了一种称为矩阵几何解的分析方法。对此进行分析QBD过程，设过程Q正常返，当且仅当矩阵方程

$R^{2}B+RA+C=0$ . (4)

最小非负解R的谱半径 $SP\left(R\right)<1$ ，R称为率阵，Neuts [19] 给出了R的概率解释，且Neuts [18] 给出了详细的证明。因为系数(4)都是上三角矩阵，我们可以假设R具有相同的结构

$R=\left(\begin{array}{cc}{r}_{11}& r_{12}\\ 0& r_{22}\end{array}\right)$ , (5)

将 $R^2$ 和R代入(4)，我们得到以下结果

$R=\left(\begin{array}{cc}{\sigma }_0& {\rho }_0\\ 0& {\rho }_1\end{array}\right)$ , (6)

和

$R^n=\left(\begin{array}{cc}{\sigma }_0^n& {\rho }_0{\displaystyle \underset{j=0}{\overset{n-1}{\sum }}{\sigma }_0^j{\rho }_1^{n-j-1}}\\ 0& {\rho }_1^n\end{array}\right)$ , (7)

其中由于R的谱半径小于1，而 ${\sigma }_0$ 较大根大于1，所以取较小根，则

$\begin{array}{l}{\sigma }_0=\frac{\theta +\lambda q_0-\sqrt{{\left(\theta +\lambda q_0\right)}^2-4\eta \lambda q_0}}{2\eta },\\ {\rho }_0=\frac{1+{\sigma }_0}{1-{\sigma }_0}\frac{\theta }{\mu },\\ {\rho }_1=\frac{\lambda q_1}{\mu },\end{array}$ (8)

定义极限概率为

${\pi }_{ni}=\underset{t\to \infty }{\lim }P\left\{N\left(t\right)=n,J(t)=i\right\},\left(n,i\right)\in \Omega$ , (9)

${\pi }_n=\left({\pi }_{n0},{\pi }_{n1}\right),n\ge 0$ . (10)

定理2.1：转移概率矩阵形如(2)的马尔可夫链 $\left\{\left(N\left(t\right),J\left(t\right)\right),t>0\right\}$ 正常返，假设 ${\rho }_1<1$ 和 ${\rho }_1\ne {\sigma }_0$ 则平稳概率如下

${\pi }_{n0}=K{\sigma }_0^n,n\ge 0$ , (11)

${\pi }_{n1}=K\left({\rho }_0\frac{{\sigma }_0^n-{\rho }_1^n}{{\sigma }_0^{}-{\rho }_1^{}}+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }{\rho }_1^n\right),n\ge 0$ , (12)

其中

$K=\left(1-{\sigma }_0\right)\left(1-{\rho }_1\right){\left(1-{\rho }_1+{\rho }_0+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }\left(1-{\sigma }_0\right)\right)}^{-1}$ . (13)

证明：系统的稳态概率向量满足 $\{\begin{array}{l}\pi Q=0\\ \pi e=1\end{array}$ ，由Neuts [17] 的矩阵几何理论可知

${\pi }_n=\left({\pi }_{n0},{\pi }_{n1}\right)=\left({\pi }_{00},{\pi }_{01}\right)R^n,n\ge 1$ , (14)

以及 $\left({\pi }_{00},{\pi }_{01}\right)$ 满足方程

$\left({\pi }_{00},{\pi }_{01}\right)B\left[R\right]=0$ , (15)

其中 $B\left[R\right]=A_0+RB$ 。求解(15)，并令 ${\pi }_{00}=K$ ，可得

$\left({\pi }_{00},{\pi }_{01}\right)=K\left(1,\frac{\lambda q_0-{\sigma }_0\eta }{\xi }\right)$ , (16)

经过(15)和(16)，我们获得

${\pi }_{n0}=K{\sigma }_0^n,n\ge 0$ , (17)

${\pi }_{n1}=K\left({\rho }_0\frac{{\sigma }_0^n-{\rho }_1^n}{{\sigma }_0^{}-{\rho }_1^{}}+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }{\rho }_1^n\right),n\ge 0$ , (18)

最后， ${\pi }_{00}=K$ 可以通过正规化条件 $\left({\pi }_{00},{\pi }_{01}\right){\left(I-R\right)}^{-1}e=1$ 确定。证毕。

从(11)和(12)，我们得到服务器处于状态 $i\left(i=0,1\right)$ 的稳态概率，记为 $p_i$ ，将(17)和(18)代入，可得

$p_0={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\pi }_{n0}}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}K{\sigma }_0^n}=\frac{K}{1-{\sigma }_0}$ , (19)

$\begin{array}{c}{p}_1={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\pi }_{n1}}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}K\left({\rho }_0\frac{{\sigma }_0^n-{\rho }_1^n}{{\sigma }_0^{}-{\rho }_1^{}}+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }{\rho }_1^n\right)}\\ =K\left({\rho }_0\frac{1/\left(1-{\sigma }_0\right)-1/\left(1-{\rho }_1\right)}{{\sigma }_0-{\rho }_1}+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }\frac{1}{1-{\rho }_1}\right)\\ =K\left({\rho }_0\frac{1}{\left(1-{\sigma }_0\right)\left(1-{\rho }_1\right)}+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }\frac{1}{1-{\rho }_1}\right),\end{array}$ (20)

则有效到达率是

$\bar{\lambda }=\lambda \left(p_0{q}_0+p_1{q}_1\right)$ , (21)

将(19)，(20)代入，可得

$\begin{array}{c}\bar{\lambda }=\lambda \frac{\xi \left[q_0\left(1-{\rho }_1\right)+{\rho }_0{q}_1\right]+q_1\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)}{\xi \left(1-{\rho }_1+{\rho }_0\right)+\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)}\\ =\lambda \frac{\xi \left[q_0\mu \left(1-{\sigma }_0\right)-\lambda q_0{q}_1\left(1-{\sigma }_0\right)+\theta q_1\left(1+{\sigma }_0\right)\right]+\mu q_1\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2}{\xi \left[\mu \left(1-{\sigma }_0\right)-\lambda q_1\left(1-{\sigma }_0\right)+\theta \left(1+{\sigma }_0\right)\right]+\mu \left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2},\end{array}$ (22)

其中 ${\sigma }_0=\frac{\theta +\lambda q_0-\sqrt{{\left(\theta +\lambda q_0\right)}^2-4\eta \lambda q_0}}{2\eta }$ 。

记 $L\left(z\right)$ 为系统的稳态队长的母函数，则

$L\left(z\right)={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{z}^n\left({\pi }_{n0}+{\pi }_{n1}\right)}$ , (23)

将(17)，(18)代入，可得

$\begin{array}{c}L\left(z\right)={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{z}^{n}K\left({\sigma }_0^n+{\rho }_0\frac{{\sigma }_0^n-{\rho }_1^n}{{\sigma }_0-{\rho }_1}+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }{\rho }_1^n\right)}\\ =K\left(\frac{1}{1-{\sigma }_{0}z}+{\rho }_0\frac{z}{\left(1-{\sigma }_{0}z\right)\left(1-{\rho }_{1}z\right)}+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }\frac{1}{1-{\rho }_{1}z}\right)\\ =\frac{1-{\rho }_1}{1-{\rho }_{1}z}\frac{K}{1-{\rho }_1}\left(\frac{1-{\rho }_{1}z}{1-{\sigma }_{0}z}+\frac{{\rho }_{0}z}{1-{\sigma }_{0}z}+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }\right)\\ =\frac{1-{\rho }_1}{1-{\rho }_{1}z}\frac{K}{\left(1-{\rho }_1\right)\left(1-{\sigma }_0\right)}\left(\left(1-{\rho }_{1}z+{\rho }_{0}z\right)\frac{1-{\sigma }_0}{1-{\sigma }_{0}z}+\frac{\lambda q_0-{\sigma }_0\eta }{\xi }\left(1-{\sigma }_0\right)\right),\end{array}$ (24)

其中 ${\sigma }_0=\frac{\theta +\lambda q_0-\sqrt{{\left(\theta +\lambda q_0\right)}^2-4\eta \lambda q_0}}{2\eta }$ 。

通过随机分解理论，得到了系统中顾客的平均数量，记为 $L\left(q_0,q_1\right)$ ，可得

$L\left(q_0,q_1\right)=\frac{{\rho }_1}{1-{\rho }_1}+\frac{\xi \left(2{\rho }_0+{\rho }_1{}^2{\sigma }_0-{\sigma }_0{\rho }_0{\rho }_1-2{\rho }_1{\sigma }_0\right)+{\rho }_1\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2}{\left(1-{\rho }_1\right)\left(1-{\sigma }_0\right)\left[\xi \left(1-{\rho }_1+{\rho }_0\right)+\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)\right]}$ , (25)

其中 ${\sigma }_0=\frac{\theta +\lambda q_0-\sqrt{{\left(\theta +\lambda q_0\right)}^2-4\eta \lambda q_0}}{2\eta }$ ， ${\rho }_0=\frac{1+{\sigma }_0}{1-{\sigma }_0}\frac{\theta }{\mu }$ ， ${\rho }_1=\frac{\lambda q_1}{\mu }$ 。

因此，可以使用利特尔定律获得决定在某一顾客到达时进入的顾客的平均逗留时间：

$W\left(q_0,q_1\right)=\frac{L\left(q_0,q_1\right)}{\bar{\lambda }}$ , (26)

将(22)，(25)代入，可得

$\begin{array}{c}W\left(q_0,q_1\right)=\frac{1}{\lambda }\frac{{\rho }_1\left[\xi \left(1-{\rho }_1+{\rho }_0\right)+\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)\right]}{\left[\xi \left(q_0\left(1-{\rho }_1\right)+{\rho }_0{q}_1\right)+q_1\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)\right]\left(1-{\rho }_1\right)}\\ +\frac{\xi \left(2{\rho }_0+{\rho }_1{}^2{\sigma }_0-{\sigma }_0{\rho }_0{\rho }_1-2{\rho }_1{\sigma }_0\right)+{\rho }_1\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2}{\left[\xi \left(q_0\left(1-{\rho }_1\right)+{\rho }_0{q}_1\right)+q_1\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)\right]\left(1-{\rho }_1\right)\left(1-{\sigma }_0\right)},\end{array}$ (27)

其中 ${\sigma }_0=\frac{\theta +\lambda q_0-\sqrt{{\left(\theta +\lambda q_0\right)}^2-4\eta \lambda q_0}}{2\eta }$ ， ${\rho }_0=\frac{1+{\sigma }_0}{1-{\sigma }_0}\frac{\theta }{\mu }$ ， ${\rho }_1=\frac{\lambda q_1}{\mu }$ 。

现在可以计算出所有顾客都遵循混合策略 $\left(q_0,q_1\right)$ 时的社会收益

$S_{au}\left(q_0,q_1\right)=\bar{\lambda }\left(R-CW\left(q_0,q_1\right)\right)=\bar{\lambda }R-CL\left(q_0,q_1\right)$ , (28)

将(22)，(25)代入，可得

$\begin{array}{c}{S}_{au}\left(q_0,q_1\right)=\lambda \frac{\xi \left[q_0\left(1-{\rho }_1\right)+{\rho }_0{q}_1\right]+q_1\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)}{\xi \left(1-{\rho }_1+{\rho }_0\right)+\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)}R\\ -C\left(\frac{{\rho }_1}{1-{\rho }_1}+\frac{\xi \left(2{\rho }_0+{\rho }_1{}^2{\sigma }_0-{\sigma }_0{\rho }_0{\rho }_1-2{\rho }_1{\sigma }_0\right)+{\rho }_1\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2}{\left(1-{\rho }_1\right)\left(1-{\sigma }_0\right)\left[\xi \left(1-{\rho }_1+{\rho }_0\right)+\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)\right]}\right),\end{array}$ (29)

其中 ${\sigma }_0=\frac{\theta +\lambda q_0-\sqrt{{\left(\theta +\lambda q_0\right)}^2-4\eta \lambda q_0}}{2\eta }$ ， ${\rho }_0=\frac{1+{\sigma }_0}{1-{\sigma }_0}\frac{\theta }{\mu }$ ， ${\rho }_1=\frac{\lambda q_1}{\mu }$ 。

系统管理者的目标是最大化整体社会收益。即求解非线性规划问题 $S_{au}\left(q_0,q_1\right)$ ( $0\le q_i\le 1,i=0,1$ )的最大值，即可以获得社会最优策略 $\left(q_0^{*},q_1^{*}\right)$ 以最大化社会收益。令

$f=f\left(q_0,q_1\right)=\xi \left(2{\rho }_0+{\rho }_1{}^2{\sigma }_0-{\sigma }_0{\rho }_0{\rho }_1-2{\rho }_1{\sigma }_0\right)+{\rho }_1\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2$ , (30)

$g=g\left(q_0,q_1\right)=\left(1-{\rho }_1\right)\left(1-{\sigma }_0\right)\left[\xi \left(1-{\rho }_1+{\rho }_0\right)+\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)\right]$ , (31)

则f，g关于 $q_0$ ， $q_1$ 的一阶导分别为

$\begin{array}{c}\frac{\partial f}{\partial q_0}=\frac{\xi {{\sigma }^{\prime }}_0}{\mu }\left(\frac{4\theta }{{\left(1-{\sigma }_0\right)}^2}+\frac{{\lambda }^2{q}_1^2}{\mu }-\frac{\left(1+{\sigma }_0\right)\theta \lambda q_1}{\mu \left(1-{\sigma }_0\right)}-\frac{2{\sigma }_0\theta \lambda q_1}{\mu {\left(1-{\sigma }_0\right)}^2}\right)\\ +\frac{\lambda q_1\left(1-{\sigma }_0\right)}{\mu }\left[\left(\lambda -{{\sigma }^{\prime }}_0\eta \right)\left(1-{\sigma }_0\right)+2{{\sigma }^{\prime }}_0\left(\lambda q_0-{\sigma }_0\eta \right)\right],\end{array}$ (32)

$\frac{\partial f}{\partial q_1}=\frac{\xi \lambda {\sigma }_0}{{\mu }^2}\left(2\lambda q_1-\theta \frac{1+{\sigma }_0}{1-{\sigma }_0}\right)+\frac{\lambda }{\mu }\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2$ , (33)

$\begin{array}{c}\frac{\partial g}{\partial q_0}=\left(\frac{\lambda q_1}{\mu }-1\right)[{{\sigma }^{\prime }}_0\left(\xi \left(1-\frac{\lambda q_1}{\mu }+\frac{1+{\sigma }_0}{1-{\sigma }_0}\frac{\theta }{\mu }\right)+\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)\right)\\ +\left({\sigma }_0-1\right)\left(\frac{2\xi \theta {{\sigma }^{\prime }}_0}{\mu {\left(1-{\sigma }_0\right)}^2}+\left(\lambda -{{\sigma }^{\prime }}_0\eta \right)\left(1-{\sigma }_0\right)-{{\sigma }^{\prime }}_0\left(\lambda q_0-{\sigma }_0\eta \right)\right)],\end{array}$ (34)

$\frac{\partial g}{\partial q_1}=\left(1-{\sigma }_0\right)[\frac{-\lambda }{\mu }\left(\xi \left(1-\frac{\lambda q_1}{\mu }+\frac{1+{\sigma }_0}{1-{\sigma }_0}\frac{\theta }{\mu }\right)+\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)\right)+\frac{\xi \lambda }{\mu }\left(\frac{\lambda q_1}{\mu }-1\right)],$ (35)

将(30)，(31)代入 $\bar{\lambda }$ 和 $L\left(q_0,q_1\right)$ ，可得

$\begin{array}{c}\bar{\lambda }=\lambda \frac{\xi \left[q_0\left(1-{\rho }_1\right)+{\rho }_0{q}_1\right]+q_1\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)}{g\left(q_0,q_1\right)/\left(1-{\rho }_1\right)\left(1-{\sigma }_0\right)}\\ =\frac{\lambda }{{\mu }^2}\frac{\left(\mu -\lambda q_1\right)\left[\xi \left(q_0\left(\mu -\lambda q_1\right)\left(1-{\sigma }_0\right)+\theta q_1\left(1+{\sigma }_0\right)\right)+\mu q_1\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2\right]}{g\left(q_0,q_1\right)},\end{array}$ (36)

$L\left(q_0,q_1\right)=\frac{\lambda q_1}{\mu -\lambda q_1}+\frac{f\left(q_0,q_1\right)}{g\left(q_0,q_1\right)}$ , (37)

所以社会收益 $S_{au}\left(q_0,q_1\right)$ 可以表示为

$S_{au}\left(q_0,q_1\right)=\lambda \frac{\xi \left[q_0\left(1-{\rho }_1\right)+{\rho }_0{q}_1\right]+q_1\left(\lambda q_0-{\sigma }_0\eta \right)\left(1-{\sigma }_0\right)}{g\left(q_0,q_1\right)/\left[\left(1-{\rho }_1\right)\left(1-{\sigma }_0\right)\right]}R-C\left(\frac{\lambda q_1}{\mu -\lambda q_1}+\frac{f\left(q_0,q_1\right)}{g\left(q_0,q_1\right)}\right),$ (38)

其中 ${\sigma }_0=\frac{\theta +\lambda q_0-\sqrt{{\left(\theta +\lambda q_0\right)}^2-4\eta \lambda q_0}}{2\eta }$ ， ${\rho }_0=\frac{1+{\sigma }_0}{1-{\sigma }_0}\frac{\theta }{\mu }$ ， ${\rho }_1=\frac{\lambda q_1}{\mu }$ 。

则 $S_{au}\left(q_0,q_1\right)$ 中 $\bar{\lambda }$ 和 $L$ 的关于 $q_0$ 和 $q_1$ 的一阶偏导数可以表示为

$\begin{array}{c}\frac{\partial \bar{\lambda }}{\partial q_0}=\frac{\lambda \left(\mu -\lambda q_1\right)}{{\mu }^2}[\frac{\xi \left(\mu -\lambda q_1\right){\left(1-{\sigma }_0-q_0{\sigma }^{\prime }\right)}_0}{g}\underset{}{\overset{\begin{array}{l}\\ \end{array}}{}}\\ +\frac{\mu q_1\left(1-{\sigma }_0\right)\left[\left(\lambda -{{\sigma }^{\prime }}_0\eta \right)\left(1-{\sigma }_0\right)-2{{\sigma }^{\prime }}_0\left(\lambda q_0-{\sigma }_0\eta \right)\right]}{g}\\ -\frac{\left[\left(\mu -\lambda q_1\right)\left(\xi \left(q_0\left(\mu -\lambda q_1\right)\left(1-{\sigma }_0\right)+\theta q_1\left(1+{\sigma }_0\right)\right)+\mu q_1\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2\right)\right]{g^{\prime }}_0}{g^2}],\end{array}$ (39)

$\begin{array}{c}\frac{\partial \bar{\lambda }}{\partial q_1}=\frac{\lambda }{{\mu }^2}[\frac{\left(\mu -\lambda q_1\right)\left[\xi q_0\lambda \left(1-{\sigma }_0\right)+\xi \theta \left(1+{\sigma }_0\right)+\mu {\left(1-{\sigma }_0\right)}^2\left(\lambda q_0-{\sigma }_0\eta \right)\right]}{g}\\ -\lambda \frac{\xi \lambda q_0{q}_1\left({\sigma }_0-1\right)+\xi \theta q_1\left(1+{\sigma }_0\right)+\mu q_1\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2}{g}\\ -\frac{\left[\left(\mu -\lambda q_1\right)\left(\xi \left(q_0\left(\mu -\lambda q_1\right)\left(1-{\sigma }_0\right)+\theta q_1\left(1+{\sigma }_0\right)\right)+\mu q_1\left(\lambda q_0-{\sigma }_0\eta \right){\left(1-{\sigma }_0\right)}^2\right)\right]{g^{\prime }}_1}{g^2}],\end{array}$ (40)

$\frac{\partial L}{\partial q_0}=\frac{{f^{\prime }}_0}{g}-\frac{f{g^{\prime }}_0}{g^2}$ , (41)

$\frac{\partial L}{\partial q_1}=\frac{\mu \lambda }{{\left(\mu -\lambda q_1\right)}^2}+\frac{{f^{\prime }}_1}{g_1}-\frac{f{g^{\prime }}_1}{g^2}$ , (42)

因此， $S_{au}\left(q_0,q_1\right)$ 的偏导数可以表示为

$\frac{\partial S_{au}}{\partial q_0}=R\frac{\partial \bar{\lambda }}{\partial q_0}-C\frac{\partial L}{\partial q_0}$ , (43)

$\frac{\partial S_{au}}{\partial q_1}=R\frac{\partial \bar{\lambda }}{\partial q_1}-C\frac{\partial L}{\partial q_1}$ , (44)

$D_1=\frac{{\partial }^2{S}_{au}}{\partial q_0^2}=R\frac{{\partial }^2\bar{\lambda }}{\partial q_0^2}-C\frac{{\partial }^{2}L}{\partial q_0^2}$ , (45)

$D_2=\frac{{\partial }^2{S}_{au}}{\partial q_0\partial q_1}=\frac{{\partial }^2{S}_{au}}{\partial q_1\partial q_0}=R\frac{{\partial }^2\bar{\lambda }}{\partial q_1\partial q_0}-C\frac{{\partial }^{2}L}{\partial q_1\partial q_0}$ , (46)

$D_3=\frac{{\partial }^2{S}_{au}}{\partial q_1^2}=R\frac{{\partial }^2\bar{\lambda }}{\partial q_1^2}-C\frac{{\partial }^{2}L}{\partial q_1^2}$ . (47)

由于目标函数表达式比较复杂，我们只提供了一个特定的充分条件来保证社会收益 $S_{au}\left(q_0,q_1\right)$ 是一个凸函数，在这种情况下我们能够得到最优加入概率 $\left(q_0,q_1\right)$ 的值。

定理2.2：如果 $D_1<0$ 且 $D_1{D}_3-D_2^2>0$ ，则关于 $S_{au}\left(q_0,q_1\right)$ 优化的问题是一个凸最大化问题，并且存在唯一的最优加入策略 $q_i^{*}\in \left[0,1\right]$ ， $i=0,1$ 。

证明： $S_{au}\left(q_0,q_1\right)$ 的优化问题有3个约束： $0\le q_i\le 1\left(i=0,1\right)$ 和 $\lambda q_1<\mu$ ，且它们都是实值线性函数。因此，约束集是凸的。

令 $H\left(q_0,q_1\right)$ 为目标函数的Hessian矩阵，其形式为

$H\left(q_0,q_1\right)=\left(\begin{array}{cc}\frac{{\partial }^2{S}_{au}}{\partial q_0^2}& \frac{{\partial }^2{S}_{au}}{\partial q_0\partial q_1}\\ \frac{{\partial }^2{S}_{au}}{\partial q_1\partial q_0}& \frac{{\partial }^2{S}_{au}}{\partial q_1^2}\end{array}\right)=\left(\begin{array}{cc}{D}_1& D_2\\ D_2& D_3\end{array}\right)$ . (48)

根据Boyd和Vandenberghe [20] 里凸函数最大化问题的理论，如果 $D_1<0$ 且 $D_1{D}_3-D_2^2>0$ 且 $H\left(q_0,q_1\right)$ 是负定的，则目标函数 $S_{au}\left(q_0,q_1\right)$ 在可行域内应该是严格凸的，这导致 $S_{au}\left(q_0,q_1\right)$ 的优化问题是一个凸函数求最大值的问题。凸函数的特点是有且仅有一个最大值。

根据上面的讨论，最优 $q_i^{*}\in \left[0,1\right]$ ， $i=0,1$ 的显式形式太长太复杂，本文只依图给出后面的数值结果。具体的求解方法可以参考Boyd和Vandenberghe等人 [20] 的研究，本文不再详细描述。图2表明社会收益 $S_{au}\left(q_0,q_1\right)$ 是严格的凸且最大值为9.98。同时我们还可以得到社会最优策略为 $\left(q_0^{*},q_1^{*}\right)=\left(0.30,0.85\right)$ 。

Figure 2. Social welfare in almost invisible situation, when R = 20, C = 1, λ = 1.2, μ = 1.5, η = 0.6, θ = 0.8, ξ = 1

图2. 几乎不可见下的社会收益，当R = 20，C = 1，λ = 1.2，μ = 1.5，η = 0.6，θ = 0.8，ξ = 1

2.2. 完全不可见情形

有两种纯策略可供顾客使用，即加入队列或不加入队列。一个策略可以用一个加入概率 $q\left(0\le q\le 1\right)$ 来描述，加入率为 $\lambda q$ 。过渡图表如图3所示。

Figure 3. Transition rate diagram in completely invisible situation

图3. 完全不可见情形下的转换速率图

当所有顾客都遵循给定策略q时，在几乎不可观察的队列中系统的平稳分布可以通过取 $q_0=q_1=q$ 。所以我们有

${\pi }_{n0}=K{\sigma }^n,n\ge 0$ , (49)

${\pi }_{n1}=K\left({\rho }_0\frac{{\sigma }^n-{\rho }_1^n}{{\sigma }^n-{\rho }_1}+\frac{\lambda q-\sigma \eta }{\xi }{\rho }_1^n\right),n\ge 0$ , (50)

其中

$\begin{array}{c}\sigma =\frac{\theta +\lambda q-\sqrt{{\left(\theta +\lambda q\right)}^2-4\eta \lambda q}}{2\eta },\\ {\rho }_0=\frac{1+\sigma }{1-\sigma }\frac{\theta }{\mu },\\ {\rho }_1=\frac{\lambda q}{\mu },\\ K=\left(1-\sigma \right)\left(1-{\rho }_1\right){\left(1-{\rho }_1+{\rho }_0+\frac{\lambda q-\sigma \eta }{\xi }\left(1-\sigma \right)\right)}^{-1},\end{array}$ (51)

可以得到平均队列长度，表示为 $L\left(q\right)$ ，如下：

$\begin{array}{c}L\left(q\right)=\frac{{\rho }_1}{1-{\rho }_1}+\frac{\xi \left(2{\rho }_0+{\rho }_1{}^2\sigma -\sigma {\rho }_0{\rho }_1-2{\rho }_1\sigma \right)+{\rho }_1\left(\lambda q-\sigma \eta \right){\left(1-\sigma \right)}^2}{\left(1-{\rho }_1\right)\left(1-\sigma \right)\left(\xi \left(1-{\rho }_1+{\rho }_0\right)+\left(\lambda q-\sigma \eta \right)\left(1-\sigma \right)\right)}\\ =\frac{\lambda q}{\mu -\lambda q}+\frac{\xi \left[\theta \left(1+\sigma \right)\left(2\mu -\sigma \lambda q\right)+\sigma \lambda q\left(1-\sigma \right)\left(\lambda q-2\mu \right)\right]+\mu \lambda q\left(\lambda q-\sigma \eta \right){\left(1-\sigma \right)}^3}{\left(\mu -\lambda q\right)\left(1-\sigma \right)\left[\xi \left(\left(\mu -\lambda q\right)\left(1-\sigma \right)+\theta \left(1+\sigma \right)\right)+\mu \left(\lambda q-\sigma \eta \right){\left(1-\sigma \right)}^2\right]}\end{array}$ (52)

根据利特尔定律，可求出顾客到达后决定进入的平均逗留时间

$W\left(q\right)=\frac{L\left(q\right)}{\lambda q}$ , (53)

将(52)代入，可得

$W\left(q\right)=\frac{1}{\mu -\lambda q}+\frac{\xi \left[\theta \left(1+\sigma \right)\left(2\mu -\sigma \lambda q\right)+\sigma \lambda q\left(1-\sigma \right)\left(\lambda q-2\mu \right)\right]+\mu \lambda q\left(\lambda q-\sigma \eta \right){\left(1-\sigma \right)}^3}{\lambda q\left(\mu -\lambda q\right)\left(1-\sigma \right)\left[\xi \left(\left(\mu -\lambda q\right)\left(1-\sigma \right)+\theta \left(1+\sigma \right)\right)+\mu \left(\lambda q-\sigma \eta \right){\left(1-\sigma \right)}^2\right]}$ , (54)

因此，单位时间的社会收益可以计算为

$S_{fu}\left(q\right)=\lambda q\left(R-CW\left(q\right)\right)$ , (55)

将(54)代入，可得

$S_{fu}\left(q\right)=\lambda qR-C\left(\frac{\lambda q}{\mu -\lambda q}+\frac{\xi \left[\theta \left(1+\sigma \right)\left(2\mu -\sigma \lambda q\right)+\sigma \lambda q\left(1-\sigma \right)\left(\lambda q-2\mu \right)\right]+\mu \lambda q\left(\lambda q-\sigma \eta \right){\left(1-\sigma \right)}^3}{\left(\mu -\lambda q\right)\left(1-\sigma \right)\left[\xi \left(\left(\mu -\lambda q\right)\left(1-\sigma \right)+\theta \left(1+\sigma \right)\right)+\mu \left(\lambda q-\sigma \eta \right){\left(1-\sigma \right)}^2\right]}\right),$ (56)

令 $q^{*}$ 表示社会最优加入概率，并令 $x^{*}$ 为一阶最优条件的根 ${S^{\prime }}_{fu}\left(q\right)=0$ 。他们具有以下关系：

定理2.6：若 $0<x^{*}<1$ 且 ${S^{″}}_{fu}\left(q\right)\le 0$ ，则 $q^{*}=x^{*}$ ；若 $0<x^{*}<1$ 且 ${S^{″}}_{fu}\left(q\right)>0$ 或 $x^{*}\ge 1$ ，则 $q^{*}=1$ 。

在下面的分析中，本文为了保证函数(56)是严格的凸函数，有且仅有一个最大值，将提供一个具体的假设.在这种情况下我们得到了最优的加入概率。

定理2.7：假设 $\rho <1$ 。如果 $0\le q\le 1$ 且 $2W^{\prime }\left({\lambda }_q\right)-{\lambda }_q{W}^{″}\left({\lambda }_q\right)\ge 0$ ，则

1) 社会收益 $S_{fu}\left(q\right)$ 在 $\left[q_1,q_2\right]$ 中是单峰且严格凸的，其中

$\left[q_1,q_2\right]=\left[0,1\right]\cap \left\{q|2W^{\prime }\left({\lambda }_q\right)-{\lambda }_q{W}^{″}\left({\lambda }_q\right)\ge 0\right\}$ . (57)

2) 如果 $0<x^{*}<1$ ，则 $q^{*}=x^{*}$ 。否则 $q^{*}=1$ 。

证明：让 ${\lambda }_q=\lambda q$ 。平均逗留时间 $W\left({\lambda }_q\right)$ 的前两阶导数由下式给出，令

$f\left({\lambda }_q\right)=\xi \left[\theta \left(1+\sigma \right)\left(2\mu -{\lambda }_q\sigma \right)+{\lambda }_q\sigma \left(1-\sigma \right)\left({\lambda }_q-2\mu \right)\right]+\mu {\lambda }_q\left({\lambda }_q-\sigma \eta \right){\left(1-\sigma \right)}^3$ , (58)

$g\left({\lambda }_q\right)={\lambda }_q\left(\mu -{\lambda }_q\right)\left(1-{\sigma }_q\right)\left[\xi \left(\left(\mu -{\lambda }_q\right)\left(1-\sigma \right)+\theta \left(1+\sigma \right)\right)+\mu \left({\lambda }_q-\sigma \eta \right){\left(1-\sigma \right)}^2\right]$ , (59)

其中 ${\sigma }_q=\frac{\theta +{\lambda }_q-\sqrt{\left(\theta +{\lambda }_q\right)-4\eta {\lambda }_q}}{2\eta }$ 。

则 $W\left({\lambda }_q\right)$ 关于 ${\lambda }_q$ 的一阶导数为

$W^{\prime }\left({\lambda }_q\right)=\frac{1}{{\left(\mu -{\lambda }_q\right)}^2}+\frac{f^{\prime }}{g}-\frac{f{g}^{\prime }}{g^2}$ , (60)

$W\left({\lambda }_q\right)$ 关于 ${\lambda }_q$ 的二阶导数为

$W^{″}\left({\lambda }_q\right)=\frac{2}{{\left(\mu -{\lambda }_q\right)}^3}+\frac{f^{″}}{g}-\frac{2f^{\prime }{g}^{\prime }+f{g}^{″}}{g^2}+\frac{2f{g}^{\prime }{g}^{\prime }}{g^4}$ , (61)

可计算出社会收益的二阶导数为

${S^{″}}_{fu}\left({\lambda }_q\right)=-2C{W}^{\prime }\left({\lambda }_q\right)-C{\lambda }_q{W}^{″}\left({\lambda }_q\right)=-C\left(2W^{\prime }\left({\lambda }_q\right)-{\lambda }_q{W}^{″}\left({\lambda }_q\right)\right)$ . (62)

因此，若 $2W^{\prime }\left({\lambda }_q\right)-{\lambda }_q{W}^{″}\left({\lambda }_q\right)\ge 0$ ，则 ${S^{″}}_{fu}\left({\lambda }_q\right)<0$ ，那么社会收益 $S_{fu}\left(q\right)$ 在 $\left[q_1,q_2\right]$ 中是单峰且严格凸的。

在图4，我们观察到 $S_{fu}\left(q\right)$ 首先随着q增加然后减少，并且在 $q=0.615<1$ 处具有最大值。因此，我们有 $q^{*}=0.615$ 。

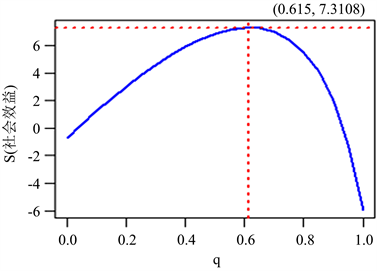
Figure 4. Social welfare in completely invisible situation, when R = 20, C = 1, λ = 1.2, μ = 1.5, η = 0.6, θ = 0.8, ξ = 1

图4. 完全不可见情形下的社会收益，当R = 20，C = 1，λ = 1.2，μ = 1.5，η = 0.6，θ = 0.8，ξ = 1

3. 数值例子

在本节中，我们提出了一些数值分析来研究社会最优加入概率的敏感性顾客和系统参数的社会最优收益。我们分析两个信息水平下最优策略下的社会收益。在图5，当λ超过一定的值时，社会收益会先增加，原因是到达率λ较小时，顾客的等待时间更短，这使得社会收益提高。而当到达率λ变大时，由于顾客的不断到达，系统会造成拥堵，此时顾客的等待时间会相对延长，那么社会收益就会开始下降，且对几乎不可见情况影响较大。图6和图7表明社会收益总是随着服务率μ和休假率θ而增加，这是直观的。这是因为顾客个人的收益变大了，社会收益也提高了。图8表明社会收益是与延迟时间ξ相关的，并呈现略微下降的趋势。这是因为较短的延迟时间会导致过多的顾客进入假期，从而导致系统拥塞并降低社会收益。图9表明社会收益是与工作休假的服务率η相关的，但社会收益随着工作休假的服务率η增大而有减小的趋势，但是对于几乎不可见影响较小，可以认为稳定，而对完全不可见影响较大，此时服务器应选择合适的η。

从这些参数的变化，我们可以发现在正常情况下 $S_{fu}\left(q\right)\le S_{au}\left(q_0^{*},q_1^{*}\right)$ ，但同时我们也能发现，有些参数不是越大越好(例如λ)或越小越好(例如η)，若参数选取的不恰当，很有可能会造成负的社会收益。所以为了得到更多社会收益，系统管理者可以适当地向顾客披露服务器的状态信息。

最后，我们关注延迟工作休假。以完全不可见队列为例，进行延迟工作休假和普通休假这两种机制的比较工作，主要对比哪种机制在控制平均队列长度和提高社会收益方面效果更好。图10表明无论是哪种机制平均队列长度 $L\left(q\right)$ 都相对于q增加，并且社会收益 $S_{fu}\left(q\right)$ 先增加后减少并且有一个最大值，如图11。另一方面，图10和图11表明普通假期的队列的平均排队长度总是小于延迟工作假期的队列，延迟工作假期的队列的社会收益总是小于普通假期的队列。

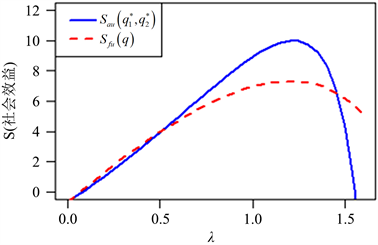
Figure 5. Social welfare, when R = 20, C = 1, μ = 1.5, η = 0.6, ξ = 1, θ = 0.8

图5. 社会收益，当R = 20，C = 1，μ = 1.5，η = 0.6，ξ = 1，θ = 0.8

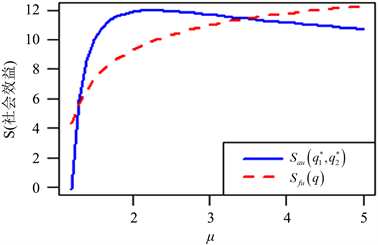
Figure 6. Social welfare, when R = 20, C = 1, λ = 1.2, η = 0.6, ξ = 1, θ = 0.8

图6. 社会收益，当R = 20，C = 1，λ = 1.2，η = 0.6，ξ = 1，θ = 0.8

Figure 7. Social welfare, when R = 20, C = 1, λ = 1.2, μ = 1.5, η = 0.6, ξ = 1

图7. 社会收益，当R = 20，C = 1，λ = 1.2，μ = 1.5，η = 0.6，ξ = 1

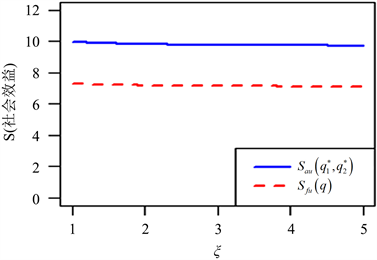
Figure 8. Social welfare, when R = 20, C = 1, λ = 1.2, μ = 1.5, η = 0.6, θ = 0.8

图8. 社会收益，当R = 20，C = 1，λ = 1.2，μ = 1.5，η = 0.6，θ = 0.8

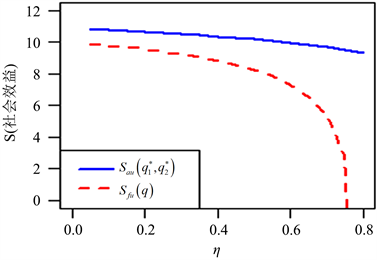
Figure 9. Social welfare, when R = 20, C = 1, λ = 1.2, μ = 1.5, ξ = 1, θ = 0.8

图9. 社会收益，当R = 20，C = 1，λ = 1.2，μ = 1.5，ξ = 1，θ = 0.8

Figure 10. Queue length in delayed working vocations and normal vocations, when R = 20, C = 1, λ = 1.2, μ = 1.5, η = 0.6, θ = 0.8, ξ = 1

图10. 延迟工作休假与普通休假排队的队长，当R = 20，C = 1，λ = 1.2，μ = 1.5，η = 0.6，θ = 0.8，ξ = 1

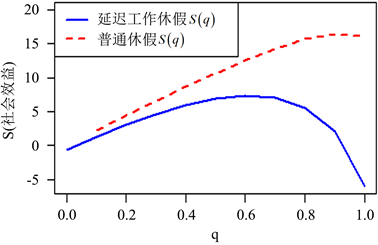
Figure 11. Social welfare in delayed working vocations and normal vocations, when R = 20, C = 1, λ = 1.2, μ = 1.5, η = 0.6, θ = 0.8, ξ = 1

图11. 延迟工作休假与普通休假排队的社会收益，当R = 20，C = 1，λ = 1.2，μ = 1.5，η = 0.6，θ = 0.8，ξ = 1

我们又对比了Tian [17] 学者研究出的延迟休假的平均队长和社会收益发现，延迟休假是优于普通休假的，这是因为在假期排队时，当系统是空的，服务器立即开始休假，顾客等待更长的时间和更大的等待成本，同时在延迟休假的队列中，系统空了之后到达的一些顾客在延迟时间内得到服务。但本文发现普通休假优于延迟工作休假。综合表明，我们给予系统一个延迟时间然后再休假是合理且高效的，但是休假期间如果维持低速率服务，那么实际上，它的平均队长会更长，社会收益会更低，甚至还不如普通的休假。总而言之，延迟休期在一定程度上缓解了系统拥堵问题，增加了社会收益，但延迟工作休假会减少社会收益。

4. 结论

在本文中，我们讨论了在几乎和完全不可见的M/M/1延迟工作假期排队系统中服务器的社会最优策略。我们在两种不同的情况下获得稳态性能指标和社会收益，用数值例子比较了在几乎可见和完全不可见的情况下各种参数对社会最优策略的影响，表明，我们给予系统一个延迟时间然后再休假是合理且高效的，从中观察到系统信息的披露对系统管理者有一定的好处。此外更为推广的研究是相对应的非马尔可夫队列。