1. 引言
拱坝是水工建筑物中一种重要的挡水坝,它以结构合理、体型优美、安全性高、经济性优越而被广泛采用。但随着坝体高度的增加,河谷地形、地质的复杂化及施工难度的提高,坝体的受力和工作状态越来越复杂,拱坝的安全性,尤其是高拱坝的安全性也越来越引起人们的关注。
坝体的应力水平是评价坝体结构安全性的一个重要指标 [1] 。拱坝结构的应力分析方法主要有拱梁法和有限单元法 [2] 。拱梁法属结构力学的方法,其力学模型有一定的简化,在坝体选型时常使用,但它无法分析坝体局部结构引起的应力变化,更难仿真坝体动态的施工力学过程。有限单元法属现代计算力学方法 [3] 。它适用于任意形状的拱坝,可以考虑复杂的地形、地质条件,可以考虑材料的塑性、开裂、流变等非线性行为,也可以很方便地模拟坝体的局部结构、混凝土浇筑顺序、横缝灌浆、温度控制、坝体蓄水等因素。所以有限单元法在拱坝的设计中得到了广泛地应用,对应有限元计算应力–等效应力的控制标准也已写入规范 [1] 。
早期,用有限单元法来计算坝体应力时,自重、水压力、温度等荷载常在坝体上一次施加,并不考虑实际的受载历程。实践表明,对于低拱坝如此加载计算的结果与实际相差不大,但对高拱坝可能会带来很大的误差,从而严重影响对坝体安全性的评价。模拟坝体施工过程的分析人们已做了较多的工作 [4] - [12] ,对自重加载模式的研究较为详细的文献有 [6] 和 [10] 。文献 [6] 以小弯拱坝为例,利用有限单元法,模拟坝体的施工过程,计算拱冠梁坝踵部位的竖向应力,结果发现自重施加方式对应力的影响较大、横缝对自重及初次蓄水对应力影响并不大(8%左右),得出的主要结论是:自重全部由梁承担过小地估计了坝体上游拉应力,而整体施加自重、水压力、计算得到的拉应力偏大。文献 [10] 通过计算坝体的主应力专门研究了自重加载方式对高拱坝的应力变形的影响,得到的结论主要是:不同的自重施加模拟方式对拱坝的应力场和位移场的影响较大,坝体的主拉应力和河床方向的位移对水平拱分层数相对于竖直分缝数目更为敏感,自重整体加载计算所得的主拉应力远大于其它自重加载方式。这些结论使我们逐渐认识了如何合理模拟坝体的自重加载过程,但还不够全面完整。一方面,文献 [6] 仅考察坝踵处的竖向应力,文献 [10] 仅考察坝体的主拉应力,拱坝是一个复杂结构,其最危险的部位并非一定在坝踵,主拉应力也仅是一个重要的评价指标;另一方面,有限元法计算的应力会受网格形状、大小、单元类型等因素的影响,且还能在一定程度上体现应力集中的现象;自重加载方案对坝体应力的影响规律可能与坝体体型有关。为此本文将以某高拱坝为例,借助ABAQUS有限元软件,计算坝体的应力,并进一步计算建基面上所有的等效应力,以此来分析坝体自重模拟的过程;在此基础上本文还考虑水荷载和温度荷载,进行非线性有限元计算,分析坝体的塑性区及塑性应变能,以求为工程设计提供一些有价值的结论。
2. 计算模型
2.1. 工程概况
某水电工程的拦河坝初步拟定为混凝土抛物线双曲拱坝,坝顶高程880.5 m,最大坝高167.5 m。优化后的拱坝体形为坝顶中心线长度288.44 m,坝顶中心角93.789˚,拱冠梁处顶拱厚度10.0 m,最大坝高处坝底厚44.81 m,厚高比0.268。坝体内共布设15道横缝,分18个坝段。水库正常蓄水位高程876.0 m,设计洪水位高程877.5 m,校核洪水位高程878.5 m,淤沙高程779.5 m。拱坝工程所在地为荒漠型大陆性气候,气温日变化剧烈。夏季极端最高气温
41.3 ℃
;冬季极端最低气温−36.4℃,坝址区多年平均气温为
7.7C
。气温年变幅温降
23.4 ℃
,温升
17.8 ℃
;库水表面多年平均温度
12.9 ℃
,年变幅
14.3 ℃
;库底水温
5.0 ℃
;下游水垫塘年均水温
8.0 ℃
。
2.2. 材料参数及模型
坝体采用C35混凝土。混凝土及岩体材料的力学参数见下表1,其中坝体横缝单元材料参数是参考其它工程及偏保守而确定的,它考虑了灌浆材料及横缝的结构。
线性有限元分析时,混凝土和岩体都采用满足广义虎克定律的线弹性材料模型;非线性有限元分析时混凝土与基岩均采用满足Drucker-Prager屈服准则的弹塑性材料,横缝采用满足Mohr-Coulomb屈服准则的弹塑性材料。
2.3. 计算荷载
计算荷载有自重、正常工况下上下游水压力、泥沙压力、温度荷载。自重按体力施加。水压力和泥沙压力按面力施加。坝体变温见下表2,它依据气象资料及规范 [1] 计算得到。
表1. 材料力学参数

Table 2. Crown filling temperate and temperature change under normal water level
表2. 封拱温度及正常水位时的变温
2.4. 计算模型
图1为整体有限元网格,节点数100,951个,单元数91,744个。图2为横缝单元,采用薄层单元来模拟,单元厚度人为设定为2 cm。计算软件为通用商业软件ABAQUS,单元类型主要是8节点6面体单元,少量6节点5面体三棱柱单元。
3. 线弹性计算结果——重力施加方式对坝体应力的影响
为便于使用等效应力来研究重力不同施加方式下的坝体应力,本节采用线弹性有限元进行计算。
3.1. 计算方案
方案1:重力整体施加。相当于坝体完建后(块体浇筑和横缝灌浆都完成)一次施加坝体自重,此时自重荷载将由拱和梁共同承担。早期有限元分析时大多如此加载,计算工作量少,效率高。
方案2:重力按梁施加。相当于坝体浇筑完成,但横缝未灌浆,各梁单独承担自身的重力。早期拱梁法大多如此加载,计算也比较简单。此方案模拟了先浇筑后灌浆的施工过程,不少低拱坝常采用此施工方法。
方案3:重力分级施加。将坝体在高度方向分10层(从下到上编号),每层高度约18 m,自重从下到上逐层施加。当施加第n层自重时,先对第n − 1层内的横缝进行灌浆,第n层中横缝未灌浆,混凝土是分块的。目前大多高拱坝都采用此施工过程。
3.2. 自重应力计算结果
为提高有限元计算应力的可靠性,在坝体建基面内也设置薄层单元,单元厚度为40 cm。由于单元形心的应力是最佳应力,所以首先用ABAQUS进行有限元分析,然后利用建基面薄层单元形心的应力通过插值得到坝体上下游面处的应力,最后再进行等效处理,等效的方法可以参考文献 [1] 和 [13] 。3个方案的坝基面最大等效应力列于表3 (表中
为第一主应力,
为第三主应力。应力以拉为正,压为负),坝体的主应力云图见图3~8。
方案3的自重施加过程比较接近于实际情况,计算结果表明左右坝肩的最大等效主拉应力大约发生在上游面807 m高程,主压应力发生在下游面725 m高程。将方案1的等效应力与方案3比较可以看到,坝底部位的应力略小于方案3,但左右坝顶拱端部位上游面的等效主拉应力远大于方案3,大约是方案3的4倍左右,下游面的等效主压应力值要小一些。这两个方案的最大等效主压应力发生的部位比较接近,但主拉应力相距较远。比较方案2与3的结果,可以发现方案2的坝底平均主压应力要大于方案3,上下游大小分布规律相反;左右坝肩的等效主拉和主压应力值都要大于方案3,压应力发生的部位比较接近,约在下游面720 m高程,最大拉应力的部位方案2要低一些,约在上游面777 m高程。这些规律从主应力的云图也可以看出。就本拱坝而言,3种方案的应力分布规律都有较大的差别,方案1、3略接近。
就以上计算结果可以得到初步结论,对于高拱坝自重整体施加会降低坝底的压应力,但对坝顶拱端的应力影响更大,可能会产生很大的拉应力,且其值远超过规范。自重按梁施加,会增加坝底的压应力,同样在左右坝肩的中部可能会出现较大的拉应力,这与自重按梁施加产生较大梁向弯矩有关。所以对于高拱坝,方案1、2的自重施加方法与实际都可能会有很大的差别,不宜采用。
3.3. 正常工况的计算结果
在自重荷载基础上继续施加水压力、泥沙及温度荷载。水压力在坝体完建后一次施加。计算正常温降和正常温升两种工况。坝基面的有限元等效主应力列于表4和表5。不少拱坝的最大等效主拉和主压应力一般发生在坝底的坝踵和坝趾处,但本拱坝并非如此,这与坝体体型及河谷形状有关。计算结果表明3种方案坝底的应力都能满足规范的要求,最大值在方案2中(温降工况等效主拉应力为1.15 MPa,主压应力为5.95 MPa)。由于本坝温差大,在坝顶拱端部位产生了很大的拉应力,尤其在温降工况,方案1左拱端的等效主拉应力大6.4 MPa,远超过规范1.5 MPa的要求。而在方案3中拱端最大等效主拉应力发生在温降工况达2.64 MPa。方案2中最大等效主拉应力发生在温升工况,达3.71 MPa,发生在左坝肩的中部。由此可见,如果采用方案1、2来计算坝体应力和设计,都将面临远大于规范值的拉应力问题,实践表明还很难通过调整体型来解决此问题;如果采用方案3则只在坝顶拱端小范围内出现超拉应力区,超过的值远小于其它两种方案。这主要是暴露在空气中的混凝土高温差带来的结果,在工程上通过保温措施是完全可以降低温度应力使其满足规范的要求,所以对于高拱坝作有限元应力分析时,自重的作用尽可能模拟实际施工过程,从而提高设计的可靠性。由于自重加载模式不同,坝体位移没有可比性,在此不作介绍。

Table 3. Maximum equivalent principal stress in dam-foundation interface
表3. 坝基面最大有限元等效主应力
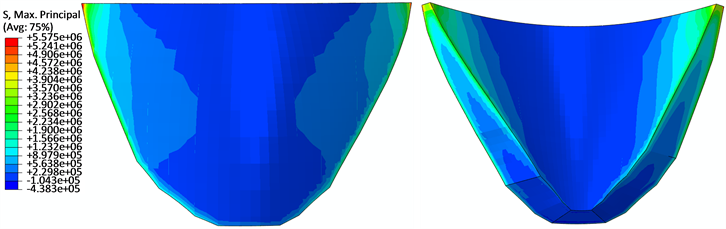
Figure 3. Program 1: Maximum principal stress of dam/Pa
图3. 方案1:坝体第一主应力/Pa
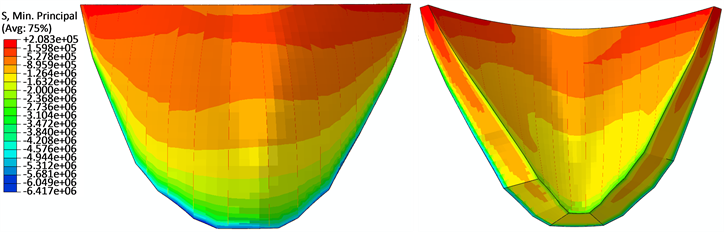
Figure 4. Program 1: Minimum principal stress of dam/Pa
图4. 方案1:坝体第三主应力/Pa

Figure 5. Program 2: Maximum principal stress of dam/Pa
图5. 方案2:坝体第一主应力/Pa
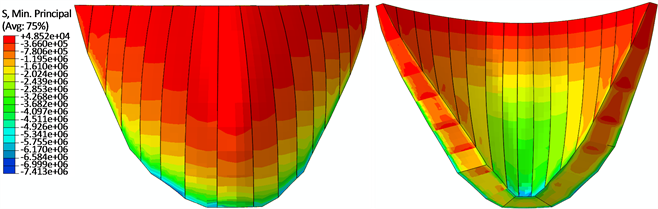
Figure 6. Program 2: Minimum principal stress of dam/Pa
图6. 方案2:坝体第三主应力/Pa

Figure 7. Program 3: Maximum principal stress of dam/Pa
图7. 方案3:坝体第一主应力/Pa

Figure 8. Program 3: Minimum principal stress of dam/Pa
图8. 方案3:坝体第三主应力/Pa

Table 4. Maximum equivalent principal stress in dam-foundation interface under normal water level and temperature drop
表4. 正常温降工况下坝基面最大等效主应力

Table 5. Maximum equivalent principal stress in dam foundation interface under normal water level and temperature rise
表5. 正常温升工况坝基面最大等效主应力
4. 非线性有限元计算结果
本节通过非线性有限元分析来进一步认识自重加载方式对坝体的影响。坝体和岩基考虑材料的非线性,材料模型见上介绍。加载过程仍假定为首先自重(有3种方案),然后是水压力和泥沙压力,最后是温度荷载,计算正常温降和温升两种工况。下表6给出了3种方案下坝体的最大等效塑性应变、塑性应变能、最大主拉和主压应力,为便于比较表中也同时列出线弹性有限元计算的最大主拉和主压应力。图9~11给出3种方案正常温降工况下坝体的等效塑性应变云图(对应温升情况的云图规律基本相同,故不再给出)。由表6可见,方案2的最大等效塑性应变比方案3约增加了40%,方案1约是方案3的2.8倍。从

Table 6. Maximum equivalent plastic strain and energy and principal stress of dam
表6. 坝体最大等效塑性应变、塑性应变能、最大主拉和主压应力
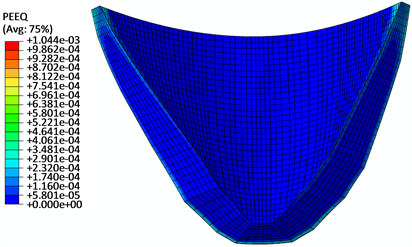
Figure 9. Program 1: Equivalent plastic strain of dam under normal water level and temperature drop
图9. 方案1:正常温降坝体等效塑性应变
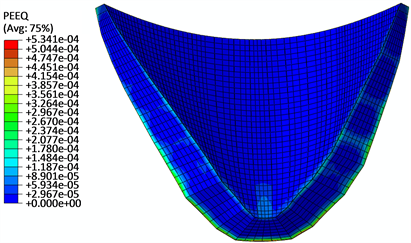
Figure 10. Program 2: Equivalent plastic strain of dam under normal water level and temperature drop
图10. 方案2:正常温降坝体等效塑性应变
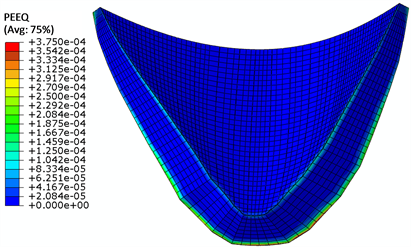
Figure 11. Program 3: Equivalent plastic strain of dam under normal water level and temperature drop
图11. 方案3:正常温降坝体等效塑性应变
等效塑性应变云图看,方案1的塑性区主要发生在坝顶拱端部位,而方案2、3的塑性区主要发生在坝体中下部的上下游表面附近,且方案2的略大。方案1、2中坝体的塑性应变能分别约是方案3的4倍和2.5倍;由此可见,自重加载的方式对坝体塑性区的分布规律、塑性应变的大小及塑性应变能都有明显的影响。从线弹性有限元的应力看,最大主拉应力发生在方案1中(温降工况),达6.93 MPa,最大压应力在方案2中,达12.22 MPa。与方案3相比主拉和主压应力分别约大30%和20%。考虑材料的非线性后,由于混凝土的屈服或开裂,坝体最大主拉应力明显减小,主压应力略增加。以上计算结果表明,方案1的加载对坝体的损伤最大,方案3最小;方案1会过高估计坝体的拉应力,尤其在坝肩上部,方案2会过高估计坝体的压应力。所以,为能真实反映坝体的工作状况,结构分析时应该考虑坝体自重的加载方式及材料的非线性。
5. 结语
本文就自重的3种施加方案,计算了坝体的线弹性有限元应力和等效应力,并进一步计算了非线性有限元应力,得到的主要结论是:对于高拱坝坝体自重的施加方式对坝体的应力、塑性区分布规律及大小都有直接的影响。自重整体施加会降低坝底部位的压应力,使抗拉要求偏保守,但更严重的可能会在坝顶拱端部位产生很大的拉应力,再遇到强温降工况其等效拉应力可能会很难满足规范要求,给设计带来很大的麻烦。自重按梁施加,尽管能提高坝底部位的压应力,但由于梁自重产生的弯矩有可能在上游建基面处产生较大的拉应力,无法满足规范要求。自重逐层施加时,坝体应力分布得到显著改善,尤其是最大拉应力会明显减小。
就本文的计算成果表明,对于高拱坝为得到坝体的可靠应力,计算时必须考虑实际的施工过程;同时,合理的施工过程可以改善坝体的实际受力,如本文的方案3就是一个比较好的施工过程。所以,研究一个合理、可行、高效、又能改善坝体受力的施工方案是很有实际意义的。本文研究的成果对其它拱坝的设计和施工都有一定的实际参考意义。