1. 引言
在电力系统中,基于铁芯气隙的电流互感器有着非常广泛的应用前景,因为它不仅能做成开合式结构,使得安装非常方便;而且,由于气隙的存在,其抗饱和能力大大增强,拓展了量程范围,同时,其非线性误差也得到明显的改善。然而,由于难以建立铁芯真实的的磁特性曲线模型,就铁芯气隙 [1] 对电流互感器的误差影响研究仍有待深化,本文正是针对这一问题,建立了气隙铁芯的磁特性曲线模型,并利用计算机仿真,得到了铁芯气隙对电流互感器的误差影响规律,从而指导了气隙铁芯电流互感器的应用。
2. 气隙铁芯的磁特性曲线模型
2.1. 闭合铁芯的磁化性能模拟
磁滞回线是铁磁材料的基本特性曲线,通过该基本特性曲线可以准确的了解铁磁材料不同工作点的磁特性。对于磁滞回线模型的建立,有基于物理机制的模型和曲线拟合的模型,其实两种方法都可以反映磁滞特性,但能够准确的反映铁磁材料的实际却都很难做到。基于物理机制的模型有J-A模型,其模型具有物理意义明确的优点,但在回线的尖端可能会出现不闭合或磁导率为负的无物理意义情况;曲线拟合的模型很多,大多都是选择一种适当的函数曲线拟合极限回环,然后将极限回环处理得到一般磁滞回环,常用的处理方法有极限回环压缩模型和极限回环平移模型等,极限回环压缩模型有磁化轨迹很容易会超出极限回环的缺点。
本文选取反正切函数加多项式结构极限回环平移模型,这种结构避免了尖端不闭合、磁导率为负和超出极限回环的问题,可以比较准确的得到各磁滞回环。
2.2. 极限磁滞回环的拟合曲线函数
一般而言,极限磁滞回环的拟合曲线函数有反正切函数和多项式结构,本文选取反正切函数加多项式结构,极限磁滞回环上行部分的函数形式为:
(1)
利用磁滞回线关于原点对称可以得到极限磁滞回环下行部分的函数为:
(2)
通过实测极限磁滞回环上的点,采用最小二乘法进行参数估计可以得到五个待定系数a、b、c、d和e。
对于顶点磁场强度为
一般磁滞回环,利用如前所述的方法,可以将极限磁滞回环沿一矢量平移得到。而该矢量至少必须满足平移后的顶点磁场强度为
,并且平移后得到的一般磁滞回环的矫顽力应等于实际矫顽力,由此可以求出该矢量。
设该矢量为
,则一般磁滞回环的上行部分为:
(3)
下行部分仍然由对称性求得:
(4)
2.3. 气隙铁芯的磁化模型
气隙铁芯的特性曲线可以由对应的闭合特性曲线模型推导而来,为了便于推导分析,作如下两点假设:
1) 气隙铁芯的截面平行且垂直于磁力线方向
2) 气隙周围没有凸出的磁力线
设闭合铁芯的磁化曲线为:
(5)
对图1的气隙铁芯,设励磁电流为
,磁感应强度为B,铁芯中的磁场强度为
,气隙中的磁场强度为
,铁芯中的平均磁路长度为
,气隙中的磁路长度为
,气隙比为
,铁芯的相对磁导率为
,真空中的磁导率为
,所以:
(6)
而气隙铁芯的等效磁场强度可表示为:
(7)
则有:
(8)
即:
(9)
上式即为气隙铁芯的磁化模型,它展示了气隙铁芯与闭合铁芯的磁特性曲线的关系。由此,在已知气隙比的情况下,可以根据闭合铁芯的磁特性曲线模型得到气隙铁芯的磁特性曲线模型,即:
(10)
3. 气隙铁芯的磁特性分析
3.1. 气隙铁芯的磁性能特点
根据前面的分析知,气隙铁芯的磁特性曲线可以由闭合铁芯的磁特性曲线推导而来,即
曲线可以通过
曲线和
曲线叠加而来。图2是在气隙比
时得到的模拟曲线。
从仿真图可以看出,当铁芯开气隙后,磁特性发生了明显的变化,具体表现在:
1) 铁芯的剩磁显著降低;
2) 铁芯的抗饱和能力增强;
3) 铁芯的磁导率减小;
4) 铁芯线性度变好。
3.2. 气隙影响磁性能的理论分析
根据上面的仿真分析知,由于气隙的存在,铁芯的磁特性发生了明显的变化,下面在气隙铁芯的磁化模型的基础上,从理论上分析气隙对铁芯剩磁特性、饱和特性、磁导率和非线性的影响。
1) 气隙对剩磁特性的影响
从上面的仿真分析知,由于气隙的存在,铁芯的剩磁显著降低,下面从极限磁滞回环对应的剩磁来理论分析气隙对剩磁特性的影响。
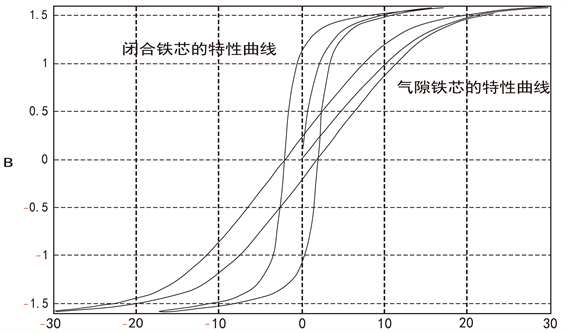
Figure 2. The comparison curve of core magnetization characteristic
图2. 铁心磁化特性曲线对比图
设闭合铁芯的极限磁滞回环的上行部分为:
(11)
利用微元法有,在
的微小领域内函数
可以认为是线性的,即在该微小领域内,函数可表示为:
(12)
根据前面的分析知,当气隙比为l时,气隙铁芯的极限磁滞回环的上行部分为:
(13)
即,
(14)
设磁场强度
时的磁感应强度即为磁滞回环对应的剩磁
,所以闭合铁芯和气隙铁芯的剩磁关系式为:
(15)
从上式可以看出,闭合铁芯的剩磁大于气隙铁芯的剩磁,而且气隙比越大,气隙铁芯的剩磁越小。
2) 气隙对饱和特性的影响
从上面的仿真分析知,由于气隙的存在,铁芯的抗饱和能力增强,下面利用磁化曲线从理论上来分析气隙对饱和特性的影响。
设铁芯本身的饱和磁感应强度为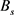 ,则可求出闭合铁芯和气隙铁芯的饱和磁场强度关系式为:
,则可求出闭合铁芯和气隙铁芯的饱和磁场强度关系式为:
(16)
从上式可以看出,气隙铁芯的饱和磁场强度大于闭合铁芯的饱和磁场强度,而且气隙比越大,气隙铁芯的饱和磁场强度越大。
3) 气隙对磁导率的影响
通过对比仿真图也可以看出,气隙铁芯的磁导率会显著减小,而磁滞回环的线性度会变好,为了从理论上详细分析气隙对磁性能的影响,下面利用微元法,将磁化曲线分为很多微小的部分段,在每个部分段可认为是线性的,如图3。
对于闭合铁芯,在非饱和区内,设磁导率最大的部分段的磁导率为
,则其表达式可写为:
(17)
设磁导率最小的部分段的磁导率为
,则其表达式可写为:
(18)
则对于气隙比为l的气隙铁芯,磁导率最大的部分段的表达式变为:
(19)

Figure 3. Differential graph of magnetization curve
图3. 磁化曲线微分图
磁导率最小的部分段的表达式变为:
(20)
所以,气隙的存在会使磁导率减小,并且气隙越大,磁导率减小得越多。
同时,对比磁导率最大部分段和磁导率最小部分段的相对变化有:
(21)
即磁导率越大的部分段,磁导率减小的越多。
4) 气隙对非线性的影响
根据上面的分段处理容易得到,在非饱和区内,闭合铁芯磁导率的线性度为:
(22)
对应的气隙铁芯磁导率的线性度为:
(23)
比较两种情况的线性度有:
(24)
即气隙铁芯磁化曲线的线性特性比闭合铁芯的线性特性好。同时,对于气隙铁芯,容易得到,气隙比l越大,线性度d越趋向于零,即线性特性越好。
4. 气隙铁芯电流互感器的建模与仿真
4.1. 气隙铁芯电流互感器的数学建模
为了便于分析,下面忽略涡流损耗的影响,则气隙铁芯电流互感器的等效电路模型示为:
图4中R为二次绕组内阻和负载电阻之和,L为二次绕组漏电感和负载电感之和。
由等效电路可列电动势平衡方程:
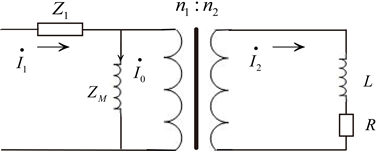
Figure 4. The equivalent circuit of air-gapped core current transformer
图4. 气隙铁心电流互感器等效电路
(25)
又根据磁动势平衡有,
(26)
又由
有,
(27)
即,
(28)
则可得到,
(29)
上式即为气隙铁芯电流互感器的数学模型。
4.2. 气隙铁芯电流互感器的仿真
根据前面的分析知道,铁芯的各磁滞回环基本上平行,并且从仿真结果得到气隙铁芯的磁滞效应相比闭合铁芯的磁滞效应减弱。所以,为了方便分析铁芯气隙对电流互感器的影响,忽略磁滞效应并用气隙铁芯的磁化曲线模型进行仿真是可行的,这样也能得出铁芯气隙对电流互感器的影响规律。
这样,在给定
的情形下,首先将方程离散化得到对应的差分方程,然后由当前
计算出对应的
,再将它们代入差分方程进行迭代求解,从而得到励磁电流
的波形,由此也可以求得
的波形。
下面是对一闭合电流互感器,在气隙后进行的对比仿真。其中闭合铁芯构成的电流互感器的相关参数为:额定变比为1000 A:5 A,一次绕组匝数为5 T,二次绕组匝数为1000 T,铁芯截面积为4 cm2,平均磁路长度为10π cm。相应的磁特性曲线根据前面的阐述的方法求得。
通过对比仿真,可以得到如下波形:
从上面的仿真图5可以看出,对于闭合铁芯电流互感器,在饱和点附近其二次电流波形已有些许畸变,而此时气隙铁芯电流互感器的波形基本上为正弦波,即气隙后电流互感器的抗饱和性能增强。图6是在不同气隙比下的二次电流波形对比仿真,从仿真图可以看出,气隙比越大,二次电流波形的幅值越
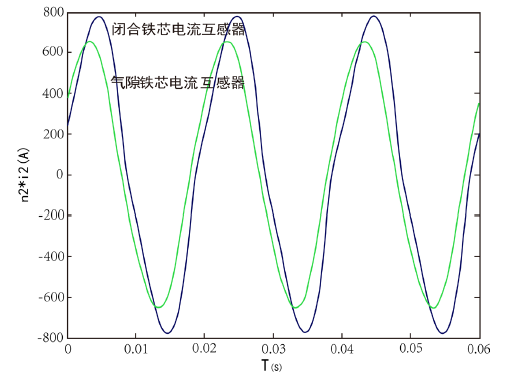
Figure 5. Waveform simulation when the air gap exists or not
图5. 有无气隙时的波形对比仿真
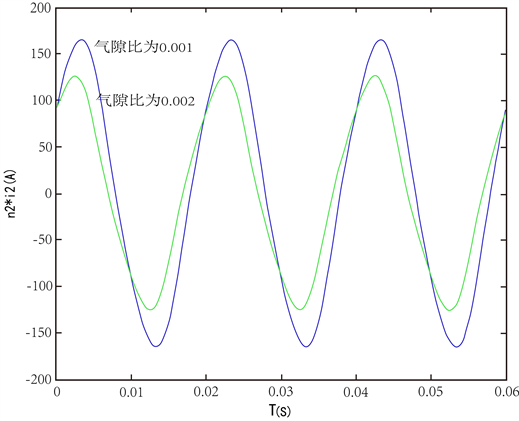
Figure 6. The waveform simulation of different air gap ratio
图6. 不同气隙比时的波形对比仿真
小,而且相位越超前,即气隙比越大,电流互感器的误差也会相应的增大,与实际情况相符。
5. 气隙铁芯电流互感器的误差分析
根据前面的仿真分析知道,气隙会对电流互感器的二次电流产生影响,从而会影响电流互感器的误差 [2] 。为了从理论上量化分析气隙对电流互感器的误差影响,下面运用自动控制理论的方法就气隙对电流互感器的误差影响进行具体的分析。
5.1. 气隙铁芯电流互感器的传递函数模型
根据前面气隙铁芯电流互感器的状态方程可以画出相应的控制框图,从而得到气隙铁芯电流互感器的传递函数模型。
气隙铁芯电流互感器的控制框为图7。
根据控制框图7可以求得气隙铁芯电流互感器的传递函数为:
(30)
对应的误差传递函数为:
(31)
就误差传递函数分析可知,磁导率
的变化会导致气隙铁芯电流互感器的误差变化。
5.2. 气隙铁芯电流互感器的误差
根据前面得到的误差传递函数公式,将其转化为频域的形式有:
(32)
则可得到电流互感器的复数误差 [3] 为:
(33)
其中比差为:
(34)

Figure 7. The control block of air-gapped core current transformer
图7. 气隙铁心电流互感器控制框图
相差为:
(35)
5.3. 气隙对误差的影响
由上面的理论分析和仿真分析可知,铁芯气隙后其磁特性会发生变化,且可根据误差函数分析气隙对互感器误差的具体影响。
下面是针对闭合铁芯构成的电流互感器,就不同的气隙比对误差大小的影响而进行的仿真。其中仍以上面的闭合铁芯构成的电流互感器进行分析。
根据前面就气隙对磁导率的影响分析知,当气隙比为l时,闭合铁芯在某部分段的磁导率k会变为
,再结合闭合铁芯构成的电流互感器的相关参数,可以作出气隙对电流互感器在额定电流时其误差大小影响的曲线图,如图8。
从比差仿真曲线图上可以看出,随着气隙比的增大,电流互感器的比差会负向变大;从相差仿真曲线图(图9)上可以看出,随着气隙比的增大,电流互感器的相差会正向变大。
5.4. 气隙对误差非线性的影响
电流互感器在不同的一次电流下其对应的磁导率 [4] 也会不同,所以电流互感器的误差是非线性变化的,而根据前面就气隙对磁导率非线性的影响分析知,气隙会使磁导率的线性(度)变好。
当
和
时,误差的变化量为:
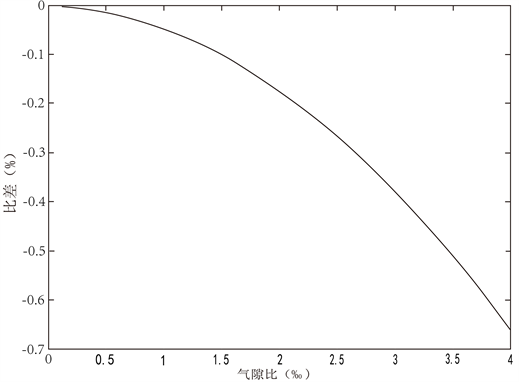
Figure 8. The relation between ratio difference of current transformer and air gap
图8. 比差随气隙变化曲线图

Figure 9. The relation between angle difference of current transformer and air gap
图9. 相差随气隙变化曲线图

Figure 10. The relation between the relative variation of angle difference and air gap
图10. 比差相对变化随气隙变化曲线
(36)
则误差的变化量占
时的误差的百分比为:
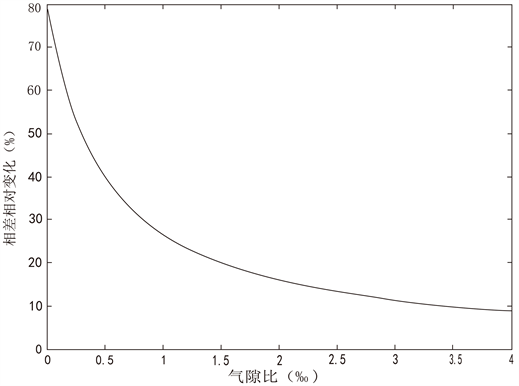
Figure 11. The relation between the relative variation of ratio difference and air gap
图11. 相差相对变化随气隙变化曲线
(37)
下面是对不同气隙比下,一次电流 [5] 在5%到100%变化时,可得到的误差相对变化的曲线图,如图10、图11。
从仿真图可以看出,随着气隙的变大,比差的相对变化和相差的相对变化都趋向于零,即气隙改善电流互感器的线性度。我们可以利用气隙铁芯的这一特性,选择一个适当的气隙,保证气隙铁芯电流互感器的非线性误差在一定范围内,从而能够较有效的提取励磁电流,这在电流互感器的补偿中将是非常有价值的。
6. 总结
本文对气隙铁芯的磁特性进行了研究,用拟合曲线函数的方法构建了其动态磁化模型,就气隙对铁芯的磁特性的影响进行了仿真分析和理论分析,在此基础上对气隙电流互感器进行了对比仿真,得到了气隙铁芯电流互感器相对于闭合铁芯电流互感器差别,以及不同气隙对电流互感器的影响,并从理论上量化分析了气隙对电流互感器误差的影响,为气隙铁芯电流互感器的设计提供了指导。