1. 引言
随着数字信号处理技术的快速发展,数字化功率因数校正技术得以快速发展,数字控制的优势在于电路简单,不需变更控制电路即可实现控制算法的修改,且容易实现较为复杂的控制算法。电感电流连续导通模式(CCM)的Boost PFC变换器具有电感电流脉动小,功率因数高,流过开关管的电流有效值小等优点,通常应用在中大功率场合 [1] [2] [3] [4] 。目前对CCM Boost PFC变换器的控制策略主要有平均电流控制、峰值电流控制、滞环电流控制等 [5] ,其中平均电流控制具有对噪声不敏感、控制精度高等优点,在APFC变换器的控制中应用广泛。本文详细分析了平均电流控制CCM Boost PFC变换器的控制原理,提出了一种数字控制的实现方法,增加输入电压前馈和占空比前馈环节实现了恒功率控制。基于数字信号控制器MC56F8257对控制策略进行了实验验证,实现了开关频率为100 kHz的单相Boost PFC的数字控制。实验结果表明,输入电压在较宽范围内变化时,变换器都能获得接近1的功率因数,从而验证了该数字控制方法的可行性。
2. 平均电流控制的原理
2.1. Boost PFC工作模式分析
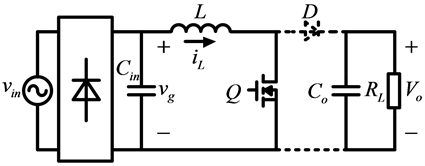
Boost PFC变换器的主功率电路如图1所示。
为了便于分析,做如下假设:1) 所有器件都是理想的;2) 输入、输出电容近似为恒压源;3) 开关频率fs远大于输入电压频率f。
Boost PFC变换器工作于电感电流连续导通模式时,在一个开关周期内,电感电流始终不会降至零,一直处于连续状态。CCM模式下的Boost PFC变换器在一个开关周期内的电感电流有两种状态:MOS管导通状态与续流二极管导通状态,等效电路图如图2所示。为了不失一般性的分析,假设此时变换器工作于第n个开关周期内,经整流桥整流后的输入电压为:
(1)
式中,Vm为输入电压的峰值,Ts为开关周期。

Figure 1. Boost PFC converter circuit
图1. Boost PFC变换器电路图
 (a)
(a)  (b)
(b)
Figure 2. Working mode of CCM Boost PFC converter. (a) Mode 1, (b) Mode 2
图2. CCM模式Boost PFC变换器工作模态:(a) 模态1,(b) 模态2
模态1:等效电路如图2(a)所示,此时MOS管导通,二极管承受反向电压关断,输出电容持续放电为负载电阻充电构成一个回路,维持输出电压恒定;输入电压为升压电感充电构成一个回路,且电感电流以斜率vg (n)/L从电流最小值处开始线性增加,电感电流和电压的表达式如式(2~3)所示。
(2)
(3)
式中,iL_initial为开关周期电感电流初始值,
。
模态2:等效电路如图2(b)所示,此时MOS管关断,续流二极管导通,电感开始放电与输入电压一起为负载供能,电感电流从峰值处开始线性减小至最小值,输出电压保持恒定,电感电流和电压的表达式如式(4~5)所示。
(4)
(5)
式中,iL_Ton为开关管开通阶段的终值,Vo为输出电压,
。
图3给出了一个开关周期内的电感电流及电压波形,在一个开关周期内,应用伏秒积平衡原理可得
(6)
式中,Ton为导通时间,Toff为关断时间。
解得占空比为
(7)
从式(7)可以看出,在CCM模式下,Boost型电路拓扑要实现功率因数校正效果,在半个工频周期内,开关管的占空比应该随着交流输入电压按正弦规律变化,当输入电压的瞬时值为零时,占空比达到最大值1,当输入电压的瞬时值达到峰值时,占空比达到最小值。但是式(7)仅是实现功率因数校正的必要条件,如果只按照式(7)控制占空比,一般不能实现输入电流正弦化的目的,通常实现的方式是给输入电流一个正弦给定,使其在相位上跟随输入电压,达到功率因数校正的目的。
2.2. 控制策略分析
图4给出了变换器的数字化控制原理框图,分为主电路和控制电路两部分。其中主电路由整流桥和
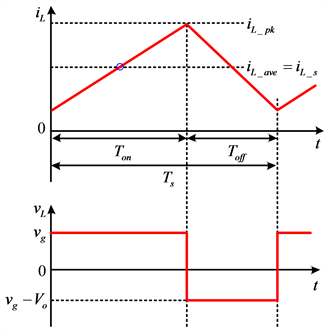
Figure 3. Inductor current and voltage waveform of CCM Boost PFC converter
图3. CCM模式Boost PFC变换器电感电流与电压波形
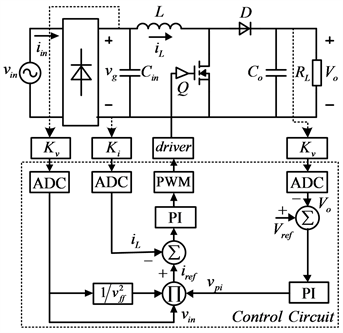
Figure 4. Average current digital control principle block diagram
图4. 平均电流数字化控制原理框图
Boost电路组成,控制电路包括采样调理电路、驱动电路和DSP周边电路。
平均电流控制算法包括电压外环和电流内环,电压外环的作用是控制变换器的输出电压稳定在参考值附近,电流内环的作用是控制电感电流的平均值跟随参考电流变化呈现正弦状,减小相位差和波形畸变因数,提高功率因数。参考图4,具体的实现过程如下。
DSC芯片MC56F8257的ADC模块采样主电路的输出电压Vo、整流后的电压Vin和电感电流iL三个模拟量。输出电压Vo与参考电压Vref比较后得到的误差信号经过电压误差放大器后作为电压外环的输出量VPI,并将它作为乘法器的一路输入;采样的整流输入电压Vin作为乘法器的第二路输入,可以得到参考电流
(8)
上式中Vff为输入电压的平均值,其计算公式为
(9)
得到的参考电流iref与采样的电感电流iL比较,产生的误差信号经过电流误差放大器得到校正占空比don。将得到的校正占空比与占空比前馈计算得到的补偿值dff相加,作为开关管占空比D送至DSC的PWM模块,即可产生控制开关管的开通关断信号。
参考电流的表达式中,VPI作为电压外环的输出信号决定了参考电流的幅值;Vin为参考电流提供了与交流输入电压同相位的正弦波作为波形基准;Vff的引入则是为了保证交流输入电压在一定范围内变换时,输出功率恒定。占空比前馈补偿环节是为了改善输入电流波形的过零畸变现象,具体原因如下节分析。
控制程序由一个主程序和一个脉冲脉宽调制(PWM)重载中断子程序组成,如图5所示,其中,主程序完成初始化、PFC启动电压判断及电压环计算,启动电压设为176 V;中断子程序完成电压采样、电流环计算、占空比更新、PWM控制信号生成,中断周期即为开关周期。
3. 数字控制的前馈环节
3.1. 输入电压前馈环节
通常电网电压的幅值会随负载变化而波形,因此考虑到电网电压的波动,需要将APFC变换器设计为宽电压范围输入。
假设输入电网电压有效值为Vac_rms,输入电流很好的跟随了电流参考值的变化,有效值为Iac_rms,则输入功率Pin为
(10)
输出功率为
(11)
式中,
为变换器的效率。
APFC变换器的输出功率在工频周期内只和负载有关,当负载不变时,输出功率应该为定值。当输入电压变化为kVac_rms时,由式(8~9)可得参考电流变为
(12)
对比
与
可得,此时的输入电流有效值为Iac_rms/k,那么输入电压变化后的输入功率为
(13)

Figure 5. Flow chart of control program
图5. 控制程序流程图
因此,当引入前馈电压环节时,输入功率不随输入电压变化,实现了恒功率控制。
3.2. 占空比前馈环节
APFC变换器在输入电压过零点附近存在输入电流畸变现象,电流畸变的主要原因是电感电流的相位超前输入电压造成的。在模拟控制中利用电容和电阻构成相位补偿网络来补偿这个相位超前 [6] ,由于这种方法需要外加电路,并没有得到很好的推广。常见的抑制输入电流畸变的方法是在电流环输出环节加上占空比前馈值,减小输入电压和输出电压对输入电流的影响。这种方法由于程序简单,尤其适合数字控制电路。
考虑输入电压Vin和输出电压Vo对电流环的影响,可以得到Boost变换器的电流响应为 [7]
(14)
如果忽略输入电压和输出电压对电流环的影响,得到的小信号模型为
(15)
对式(14~15)进行拉氏变换可得
(16)
(17)
从式(17)中可以看出占空比和电感电流成线性关系,不受输入电压和输出电压的影响,这是控制中希望得到的结果。由(16~17)式可知,将实际值与理想值做差得到前馈占空比的补偿量
为
(18)
增加的占空比补偿量代入式(16)可得
(19)
从上式可得,只要补偿的占空比表达式满足式(18)的形式,就可以消除输入电压和输出电压对电流环的影响。这里我们可以取补偿量为
(20)
4. 实验验证
为了验证数字变占空比控制的有效性,基于数字信号控制器MC56F8257对300 W的Boost PFC变换器进行了实验验证。具体电路参数为:输入交流电压有效值为Vin = 176 V − 264 V,f = 50 Hz,Vo = 400 V,fs = 100 kHz,L = 1 mH,输入滤波电容Cin = 0.22 μF,输出滤波电容Co = 560 μF。
变换器工作在额定负载功率时,其工频周期内的输入电压、输入电流及电感电流波形如图6所示。从图中可以看出电感电流的平均值跟随输入电压,输入电流基本是正弦波,与理论分析一致。
当输入电压在176~264 V AC波动时,Boost PFC变换器的输入功率与总谐波畸变率(THD)如表1所示。
从表1中可以看出,功率因数随着输入电压的增大而降低,在220 V的额定输入电压下,功率因数为0.990,THD为8.5%。当输入电压在较宽的范围内变化时,变换器的功率因数都接近于1,即验证了平均电流数字控制的正确性与可行性。
 (a)
(a)  (b)
(b)
Figure 6. Input voltage, input current and inductor current waveforms. (a) Power frequency cycles, (b) Switching cycles
图6. 输入电压电流与电感电流波形:(a) 工频周期,(b) 开关周期

Table 1. PF and THD at different input voltages
表1. 不同输入电压下的功率因数与THD
5. 结语
本文详细分析了电感电流连续模式下的平均电流控制的基本原理,推导了Boost PFC变换器实现功率因数校正的占空比表达式,提出了数字控制的实现方法,并详细解释了恒功率控制与占空比前馈的原理。基于数字信号控制器MC56F8257对额定功率为300 W的Boost PFC变换器进行了实验验证,实验结果表明,平均电流的数字控制策略可以在较宽的输入电压范围内保持功率因数接近于1,输入电流波形基本没有畸变,验证了该数字实现方法的可行性。