2. 经典Galerkin方法下的结论
2.1. 预备知识
双线性 设
是一个双线性泛函 [6] ,则
三线性设
是一个三线性泛函,则
对于
有下列性质(参见 [7] ):
2.2. Galerkin方法的弱形式
设
是一个有界区域。考虑下面定常N-S方程 [8] :
问题I求
满足
(1)
其中u表示速度,p表示压力,f表示外力,
是雷诺数的倒数,是常数。
如下记号:
问题I的变分形式为:
问题I*求
满足
其中
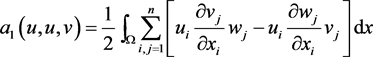 ,
,
.
设
和
分别是X和M空间中次数不超过N的多项式空间,则(1)的谱格式为:
(2)
从文献 [7] 可以得到以下结论。
定理1.1 如果Babuška不等式成立,那么
其中N为插值多项式的个数,
满足Babuška不等式。
3. 非线性Galerkin-Legendre谱方法
3.1. 准备知识
先引进一些记号。设
,
,
,
,
.
注意到
和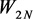 中的元素均在
处为零,即在边界上为零。
中的元素均在
处为零,即在边界上为零。
设
是
的正交投影算子,即
,
,
设
是
的投影算子,即
,
,
3.2. 非线性Galerkin-Legendre方法
问题I的非线性Galerkin-Lengedre格式为 [9]
问题I**求
,和
,使得
(3)
引理2.1根据三线性泛函的性质,有以下结论
以上引理在 [10] 中已经得证。
定理2.1 在引理2.1成立下,对充分大的N,我们有
,
其中C为与
有关的常数,K为与
有关的常数,M为与
有关的常数,
,N为插值多项式的个数。
证明:因为
的定义满足
记
,
,
.
显然
,
,
,特别地
由(1)式与(3)相减
整理得到
不妨取
,
,于是
其中
注意到
。根据Young不等式
因为
,应用Young不等式,Poincare不等式以及
,对充分大的N,有
因为
,
综上
.
由Gronwall不等式
其中
,N为基函数个数。
现在对压力作误差估计。
记
在文献 [11] 中有以下结果:
引理2.2 如果Babuška条件成立,则
下面我们根据Babuška不等式性质以及速度误差的相关结论有
(1)式减去(3)式
由Babuška不等式,找任意
,
则
注意到
,
。
因此
根据
,考虑到
与
正交,文献 [5] 有以下结论
,
因此
综上结论,我们有如下误差估计
其中C是与
有关的常数,K是与
有关的常数,M是与
有关的常数,
。
4. 数值算例
我们考虑如下的N-S方程(飞机抖振数学模型):
(4)
其中
,
,速度空间是一个狄利克雷边界,时间上使用差分法(显示欧拉格式),压强空间上用次数不超过N的多项式空间近似逼近,得到如下格式:
(5)
现对u做Legendre多项式插值,即
,
对p做Legendre多项式插值,即
、
是插值系数,
是插值基函数。
将这些近似多项式和代入上述(5),则有
这是一个线性方程组形式,算法的步骤如下:
已知方程(4)
的精确解
处理不可压缩N-S方程的谱方法与传统的变分法以及有限元法处理N-S方程的区别很明显,从表1和表2可以看出相同的时间间隔,谱方法得出来的结果比经典格式的结果更加精确;表3中的误差表

Table 1. The comparison of error estimates for velocity in two different formats with N = 16 and T = 1
表1. N = 16和T = 1两种不同格式下的速度的误差估计的比较

Table 2. The comparison of error estimates for pressure in two different formats with N = 16 and T = 1
表2. N = 16和T = 1两种不同格式下的压强的误差估计的比较

Table 3. The error estimates and convergence order for different time intervals and N with T = 1 and T = 2
表3. T = 1和T = 2时不同时间间隔和不同N的误差估计以及收敛阶
示在T = 1、T = 2时刻下的速度误差和压力误差总和,从表3中可以看出不同时间间隔下,时间间隔对方程的误差估计影响更大,该方程的收敛阶可以用
来刻画,并且速度收敛阶是1;在相同时间间隔和不同N下,N对方程的误差估计影响更大,该方程的收敛阶可以用N来刻画,且随着基函数的个数N的增加,误差越来越少,所得的精度越高,收敛结果也符合谱方法的收敛阶,以N的负指数次幂速度收敛精确解。
5. 结语
研究提出了一类求解定常纳维斯托克斯方程的谱方法,基于二维不可压缩N-S方程给出了LG格式,并且得出相关误差结果,比较了该方法与经典方法和有限元方法的区别,从数值结果我们可以发现LG谱方法下速度逼近的收敛率是最优的,而压强逼近的收敛率也很好。从表格上可以看出当解
是光滑的,即使对较小的N也能得到很好的结果,而且计算量不大,这充分体现了LG谱方法的优越性。基于N-S方程的GL方法的数值分析,可以看出对于飞机抖振问题,可以通过减少与空气阻力,达到节约能源的目的。
基金项目
贵州省科学技术基金项目(黔科合J字[2013]2128),贵州省大数据重点实验室开放课题 (2017BDKFJJ012)。
NOTES
*通讯作者。