1. 引言
在现代的数字图像技术中,二维彩色数字图像扮演着越来越重要的角色。一副二维数字图像中携带着许多可视化的有意义的数据,如果秘密图像被泄露,落入不法犯罪分子之手,将会造成极大的信息安全问题,因此信息安全问题就显得非常重要 [1] 。数字图像具有数据容量大、冗余度高、相邻像素之间的相关性强等固有特征,这些特征使得大部分的传统文本加密经典算法如DES (Data Encryption Standard)、AES (Advanced Encryption Standard)等不再适用图像加密 [2] [3] ,研究人员利用不同的技术开发了许多图像加密系统,如DNA加密 [4] [5] ,混合图像加密 [6] ,利用小波,卷积变换等加密算法 [7] [8] ,在这些技术中,混沌理论应用的最为广泛 [3] [4] [9] [10] [15] [16] [17] ,这是因为混沌映射具有初始状态敏感性、不可预测性和遍历性,这些性质可以在图像密码系统中找到相似的性质。
1989年,Matthews首次提出基于混沌系统的加密方案 [11] 。1997年,Fridrich将混沌映射应用到图像加密系统 [12] 。1998年,Fridrich利用2D混沌系统提出置乱–扩散结构的图像加密方案 [13] ,在这种结构下,首先在置换过程中对像素位置进行扰乱,以减少相邻像素之间的强相关性。之后,在扩散过程中像素值逐一改变,后一个值与前一个值相关,前后扩散两轮,类似雪崩效应。现有的图像加密算法中,此结构占据很大部分 [7] [8] [9] [10] 。文献 [14] ,首次提出将图像滤波应用在图像加密算法中,首先基于图像块的置乱,扰乱图像像素的相关性,然后在扩散过程中,使用它提出的图像滤波器的方法,对置乱后的图像进行扩散,最后部分的仿真测试显示它比一般的图像加密方案要更优良。文献 [15] ,采用的是2D henon映射加密图像,打破了传统的置乱–扩散结构,它采用两点式置乱扩散同时进行,大大的提升了密码系统的速度,并且为了抵抗选择明文和已知明文攻击,它采用了根据明文生成密钥流的方式,即不同的原图将会产生完全不同的密钥流。文献 [16] [17] ,均采用2D映射,生成混沌序列,应用在加密图像中, [16] 基于级联调制耦合(CMC)模型提出一种新的2D Logistic ICMIC耦合映射(2D-LICM),比起参数较少,轨道相对而言较简单的一维混沌映射,它的效果会更加优良, [17] 介绍的是一种新的2维Sine Logistic模型映射(2D-SLMM),它起源于Sine映射和Logistic映射,比起单独的两个映射,2D-SLMM具有较宽的混沌范围、较好的遍历性和超混沌特性。与1D混沌映射相比,它们通常包含一个变量和几个参数,并且它们的轨道很简单,因此它们的参数和初始值相对而言容易地估计,当这些映射被应用在图像加密系统中,容易被破解 [18] 。另一方面,高维混沌映射具有更多的变量和参数,通常表现出良好的超混沌性质,更适合于加密。
与像素平面置换相比,位平面置换不仅改变像素位置,而且改变像素值 [16] ,所以它拥有更好的加密效果,同时为了对抗选择明文和已知明文攻击,许多加密算法会提取图像的一些固有特征,如计算汉明距离,图像的hash值,图像的和等等,因此不同的明文,将会得到完全不同的特征 [15] [19] 。因此,根据上述分析总结,本文将利用高维的超混沌Lorenz系统,产生一系列混沌序列,基于这些序列,设计了一种位平面同时置乱—扩散的图像加密算法。位平面置乱采用循环移位,扩散采用异或和取反操作,并且设计了一个密钥产生器,更好的抵抗选择明文攻击和已知明文攻击。
本文的结构如下,在第2节,介绍超混沌Lorenz系统,给出了它的混沌吸引子与 图形,简要分析了它的动力学性质。在第3节提出基于Lorenz图像加密算法。第4节,对本文提出的加密算法进行了相关的性能分析,如密钥分析、敏感性分析、统计分析等等,基于所有仿真实验分析,本文所提出的算法,在数字图像加密中具有较好的性能。最后在第5节给出了本文的总结。
2. Hyper-Lorenz混沌系统
本节介绍4D超混沌 系统模型,它的数学定义为:
(1)
其中
是系统(1)的参数,系统的初始值范围:
,
,
,
,这些初始值将被用来当作整个系统的密钥。当
时,
系统处于超混沌状态,且当
时,(1)的4个Lyapunov指数依次为
,
,
,
。因为此时系统由两个正的Lyapunov指数,所以(1)会展现出超混沌状态,图1是(1)的几个不同平面的吸引子,图2是系统(1)的4个Lyapunov指数图。
3. 系统结构
3.1. 密钥产生器
为了满足明文攻击抵抗,比较流行的方法是取得明文的固有特征,然后将其隐藏在原始密钥流里面,这样混沌系统产生的密钥流则不仅跟初始值有关,还跟明文相关。即不同的明文会产生完全不同的密钥流。明文特征提取的方法通常包括hash值,所有像素的和,计算汉明距离等等 [19] [20] 。本文将依赖于系统的密钥和原文的SHA-256值构造一个密钥产生器,类似的算法如 [7] [15] [17] [18] [21] 。令H表示明文的hash值,按位顺序,将H分成4个部分:
,每个部分包括16个十六进制数。由(2)将每个部分转化为十进制的浮点数,使得
,图3展示了初始值的计算过程。
. (2)

Figure 2. The Lyapunov exponent diagram of the (1)
图2. (1)的Lyapunov指数图
输入初始值
作为密钥,根据(3),将所有密钥相加
. (3)
根据(4),更新所有初始值,这些初始值将被应用在迭代系统(1)中。
(4)
密钥产生器的详细结构展示在算法1。
3.2. 加密算法
图4展示R通道的算法加密结构,其余通道加密方式一样。首先由超混沌映射Lorenz产生4个跟明文相关的序列,然后将彩色明文P分解成R,G,B三个通道,再将每个通道分解成比特平面(BBD) [22] [23] ,先对每个通道的行循环移位以及异或取反扩散操作,再对每个通道的列循环移位及异或取反操作,最后将比特平面转化成像素平面(BBC),并组合三个通道,得到密图。详细步骤展现在算法2。
算法1:密钥产生器
输入:超混沌Lorenz映射的初始值x0,y0,z0,w0以及用来避免瞬态效应的参数L,和明文P;
输出:序列x1,M × N,y1,M × N,z1,M × N,w1,M × N,这些序列将被用在整个系统中;
1. 设置超混沌Lorenz映射的参数a = 10, b = 8/3, c = 28, r = −1;
2. 根据3.1,跟新初始值x0,y0,z0,w0;
3. 用更新后的初始值x0,y0,z0,w0,对超混沌Lorenz映射迭代,并得到4个序列x1,y1,z1,w1,再更新4个序列:x1 = x1 − ⌊x1⌋,y1=y1 − ⌊y1⌋,z1=z1 − ⌊z1⌋,w1=w1 − ⌊w1⌋,其中⌊ ⌋表示四舍五入。
4. 选取x,y,z,w:x = x1(L + 1:L + 1 + M × N),y = y1(L + 1:L + 1 + M × N),z = z1(L + 1:L + 1 + M × N),w = w1(L + 1:L + 1 + M × N);其中M,N表示明文大小。
算法2:图像加密
输入:明文彩色图像P,算法1中产生的混沌序列x, y, z, w;
输出:密图C;
1. 得到明文的三个通道R,G,B,并由BBD分解得到比特平面图像:Rbit,Gbit,Bbit;
2. 将Rbit,Gbit,Bbit分别变成rM,8N,gM,8N,bM,8N,并初始化矩阵RBM,8N,GBM,8N,BBM,8N;
3. 处理混沌序列x,y,z,令X = x,X = floor(X × 1014) mod 256,再将X用比特平面表示,最后将X转换为大小为M × 8N,y,z也做同样操作,得到X,Y,Z;
4. for i=1:M
5. kr = floor(abs(x(i))×105 ) mod M 对R通道的置乱扩散,floor表示向下取整;
6. tr = circshift(r(i,:)', kr)' circshift表示循环移位函数;
7. if i==1
8. RB(i,:)=bitxor(tr,r(end,:)) bitxor表示异或;
9. else
10. RB(i,:)=bitxor(bitxor(tr,RB(i-1,:)),X(i,:));
11. end
12. if w(i)>0
13. RB(i,:)=fliplr(RB(i,:) fliplr表示取反;
14. end
15. kg = floor(abs(y(i))×105) mod M对G通道的置乱扩散;
16. tg = circshift(g(i,:)', kg)'
17. if i==1
18. GB(i,:)=bitxor(tg,g(end,:))bitxor表示异或;
19. else
20. GB(i,:)=bitxor(bitxor(tg,GB(i-1,:)),Y(i,:));
21. end
22. if w(i)<0.2
23. GB(i,:)=fliplr(GB(i,:);
24. end
25. kb = floor(abs(z(i))×105) mod M 对B通道的置乱扩散;
26. tb = circshift(b(i,:)', kb)'
27. if i==1
28. BB(i,:)=bitxor(tb,b(end,:));
29. else
30. BB(i,:)=bitxor(bitxor(tb,BB(i-1,:) ),Z(i,:));
31. end
32. 接下来对三个通道(R,G,B)的列进行类似的移位异或取反操作,这边仅给出 通道,其余类似不再赘叙;
33. 初试化矩阵RBCM,8N,GBCM,8N,BBCM,8N,令A = 8 × N;
34. for i=1:8×N
35. kr = floor(abs(y(i))×108) mod A;;
36. tr = circshift(RB(:,i), kr);
37. i==1
38. RBC(:,i)=bitxor(tr,RB(:,end));
39. else
40. RBC(:,i)=bitxor(bitxor(tr,RBC(:,i-1)),Y(:,i));
41. end
42. if w(i)>0
43. RBC(:,i)=fliplr(RBC(:,i);
44. end
45. 再对G,B通道做类似的操作;
46. end
47.分别将RBC,GBC,BBC转换为像素平面矩阵,再组合成一幅密图C。
4. 仿真实验和性能分析
本文采用MatlabR2016a对本文提出的图像加密算法进行仿真实验,分别对彩色图Lena,Tiffany,Mandrill用本文提出的算法用密钥key进行加密,它们的图像尺寸均为512 × 512,其实验结果如图5,

Figure 5. (a) - (h) correspond to the plain-text, cipher-text image and decrypted image of Lena (a), Tiffany (d), Mandrill (g), respectively
图5. (a)~(h)分别对应Lena (a),Tiffany (d),Mandrill (g)的明文、密文图像和解密图像
从解密与加密图可以看出,所有密文呈现杂乱无章且无明显纹理,直观上说明我们的算法加密效果可行。
4.1. 统计分析
本节将通过直方图、相邻像素之间的相关性和信息熵这几个方面来评估算法抵抗统计攻击的能力。
4.1.1. 直方图分析
图像的直方图反映了一副图像像素值的分布情况,为了对抗统计分析的强力攻击,图像的直方图最好是接近完全一致分布的,且与原图的直方图相比具有显著差异,对一幅数字彩色图像,则可以将其红、绿、蓝三个通道各看作一幅特殊的灰度图像,用灰度图像的一维直方图方法去分析加密算法的性能,图6显示了 明文和密文的红、绿、蓝三个颜色通道的一维直方图。直观上可以看出,加密图像的直方图是接近完全一致分布的,且与原图具有显著差异,所以这个算法足够对抗统计分析的强力攻击。
4.1.2. 像素间的相关性分析
一般地,数字图像具有异于文本的一些固有特性如数据的高度冗余、相邻像素的相关性非常强等,攻击者往往利用这些特性对密文图像进行攻击,一个理想的图像加密算法应该产生在水平、垂直、正对角方向上的相邻像素点间相关性都比较弱的密文图像 [24] 。
设从需要考察的图像中任取N对相邻的像素点,记它们的灰度值
,则向量
和
间的相邻系数计算公式如下:
(5)
(6)
(7)
(8)
在实验分析中,我们将从明文Lena及其密图中分别随机选取5000对像素,如图7所示,明文在水平、垂直、对角方向上的相邻像素点对密集在y = x直线上,说明明文图像在各个方向上具有颇强的相关性,而密文图像在各个方向上的像素点对在整个平面中均匀散布着,说明密文图像在各个方向上相关性很弱。同时我们计算了Lena,Mandrill,Tiffany的相关性系数,结果显示在表1。两个独立不相关的序列的相关系系数理论值为0,实验结果表明明文图像相邻像素点的相关性比较高,而密文图像相邻像素点的相关性接近于0,近似无相关性。
4.1.3. 图像信息熵分析
信息熵是反映一个信息源的随机性和不可预测性的数学概念。对于数字图像来说,信息熵反映了图像信息的不确定性。假设一副图像有L种灰度值
,且各灰度值出现的概率分别为
, 则根据Shannon定理,图像的信息量为:

Table 1. The correlation coefficient between Plain image and its cipher-text in horizontal, vertical and diagonal directions, respectively.
表1. 明文与其密文分别在水平、垂直和对角方向上的相关系数

Figure 7. (a) - (c) are the distributions of plain-text and cipher-text pixels in horizontal, vertical and diagonal directions, respectively
图7. (a),(b),(c)分别为明文和密文在水平、垂直和对角方向像素的分布
(9)
称H为图像的信息熵,当图像中各灰度值出现的概率相等时,图像的信息熵最大,信息熵表示一副图像所包含信息的多少,它可以度量灰度值的分布,对于理想的随机图像,其信息熵等于8 [14] ,本文分别计算了Lena,Mandrill,Tiffany的及其相应密文的信息熵,实验结果如表2,同时将数字彩色图像的红、绿、蓝三个颜色通道图像矩阵看作为灰度图像矩阵,分别计算Lena,Mandrill,Tiffany明文图像和密文图像每个颜色通道的信息熵值,如表3所示,由表2,表3数据所示,各个密文图像和其每个通道的信息熵均接近于理论值8,由此表明本文提出的加密系统的效果非常好。
4.2. 密钥空间
密钥空间是指所有合法密钥构成的集合,图像密码系统的密钥空间应该足够大,从而可以有效地对抗穷举攻击,特别是加密解密速度非常快的密码系统,密码长度至少应该为128b [14] ,本文所提出的加密系统有5个密钥:
,设计算机精度为10−16,图像大小为512 × 512,
,则整个密
钥空间至少约为:
,这个值远远大于128b,这意味着我们的算法能够经受得住暴力破解。
4.3. 密钥敏感性
为了保证系统的安全性,一个优良的加密系统必须对密钥极端敏感,即当使用不同的密钥对密码图像进行解密时,将得不到明文。在实验中,我们将用密钥key去加密Lena,得到密图,而用几个与key差别极其微小的密钥去解密密图,如果系统足够敏感的话,是无法得到明文的,图8展示了密钥敏感性测试,同时,表4展示了用key1~key5解密图与用key加密的密图之间的NPCR和UACI。

Table 2. The results of information entropy
表2. 信息熵实验结果

Table 3. The information entropy of each color channel of different plain-texts and cipher-text
表3. 不同明文图像和分别对应本文算法得到密文图像的各颜色通道信息熵

Figure 8. Encryption sensitivity test. (a) - (f) were decrypted with key, key1 - key 5, respectively
图8. 加密敏感性测试:(a)~(f)分别为用key和key1~key 5去解密key所产生密文的明文

Table 4. The NPCR and UACI for decrypted image using different keys (Lena) (%)
表4. 用极小差别密钥解密的图片与密文的NPCR和UACI (%)
4.4. 差分分析
在图像加密系统中,差分分析指探究在相同加密密钥的条件下,密文图像会在多大程度上受明文图像的影响,攻击者通常通过选择明文分析或选择密文分析来实现差分攻击,为了测试加密系统对明文的极端敏感性,采用两个常用的度量:不同密文图像之间的像素改变率(number of pixels change rate, NPCR)和不同密文图像之间的一致改变强度(unified average changing intensity, UACI),NPCR是用来比较两幅图像相应位置的像素点的值,记录不同的像素点个数占全部像素点的比例,而UACI则是比较两幅图像相应位置的像素点的值,记录它们的差值,然后计算全部相应位置像素点的差值与最大差值(即255)的比值的平均值。在数学上,它们定义如下:
(10)
(11)
(12)
分别是图像的行数和列数,
分别是对应需要被衡量的两幅图像,本文指用同一个密钥加密仅改变一个明文像素值的两幅密图。理论上来说两幅随机图像的NPCR,UACI理论期望值分别约为99.6094%,33.4635%,本文将用彩色图像Lena和Mandrill来完成差分实验,对于每一个实验图片,将随机选取1000个像素点,每次改变一个像素值,得到一个新的图像,然后用同样的密钥去加密两个相差仅一个像素的原密钥加密仅改变一个明文像素值的两幅密图。理论上来说两幅随机图像的NPCR,UACI理论期望值分别约为99.6094%,33.4635%,本文将用彩色图像Lena和Mandrill来完成差分实验,对于每一个实验图片,将随机选取1000个像素点,每次改变一个像素值,得到一个新的图像,然后用同样的密钥去加密两个相差仅一个像素的原图,实验数据结果呈现在表5,表6以及NPCR,UACI的曲线变化图如图9所示。期望值分别约为99.6094%,33.4635%,本文将用彩色图像Lena和Mandrill来完成差分实验,同时对于明文Lena图像的每个颜色通道,随机地选取的100个像素值,对每个灰度值仅随机改变1个像素值,然后用本文提出加密算法去加密改变前后的明文图像Lena,得到对应每个颜色通道的100个NPCR,UACI曲线变化图如图10所示,实验数据结果呈现在表7。实验结果表明,本文提出的算

Table 5. The NPCR results for different image (%)
表5. 不同明文的NPCR (%)

Table 6. The UACI results for different image (%)
表6. 不同明文的UACI (%)

Table 7. The maximum, minimum, and average values of the NPCR and UACI sequences between the corresponding cipher-texts before and after the Lena image changes (%)
表7. Lena图像改变前后对应密文之间的NPCR和UACI序列的最大值、最小值和平均值(%)
 (a) (b)
(a) (b)
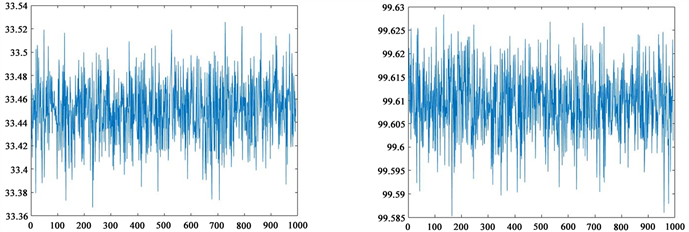
Figure 9. The NPCR and UACI of 1000 images that only change one pixel. (a) NPCR, (b) UACI
图9. 只改变一个像素值的1000张图片的NPCR和UICA,(a) NPCR,(b) UACI
法所得的NPCR,UACI值极其地接近期望值,这表明本文算法达到一个优良的扩散性能,它对原文非常敏感。所以它能够抵抗差分攻击。
5. 总结
本文提出基于高维超混沌映射的位平面彩色图像加密算法。首先通过空间相位图、Lyapunov指数图简要地分析了高维混沌映射Lorenz的动力学性质,然后基于高维混沌映射设计了一种彩色图像加密算法,在传统的置乱–扩散结构中,置乱和扩散一般是两个独立的部分,本文算法将位平面置乱和扩散同时进行,位平面置乱采用循环移位,扩散采用异或和取反操作。同时为了提高抵抗已知明文攻击和选择明文攻击的能力,与原文相关的SHA-256将应用在密钥流产生器中,因此不同的明文将产生完全不同的密钥流。最后有关本文提出算法的重要安全性能分析被提出,包括密钥分析、敏感性分析和统计分析等,所有的实验结果均表明,本文提出算法具有较强的鲁棒性,因而具有一定的应用价值。
NOTES
*通讯作者。