1. 引言
在现代相控阵雷达特别是多功能相控阵雷达中,阵元数一般为数千;此时无法采用同等数量的接收通道,只能采用子阵结构,即在每个子阵后接一个接收通道并进行数字化,为此只能得到子阵的数字化输出 [1] 。将阵列划分为子阵后,有效降低了系统成本并信号处理的维数;实际应用中,从成本和运算量考虑,子阵数一般取为几十。
对于子阵级相控阵,根据其阵列结构和组成特点,通常在阵元级采用幅度锥削加权抑制和方向图的旁瓣;而其它处理(如超分辨测向、干扰抑制等)均在子阵级进行 [2] [3] [4] 。
相控阵雷达中,子阵结构对系统性能有十分显著的影响。对相控阵雷达进行最优子阵划分是具有重要理论与实际应用意义的课题。但是,在阵列复杂度一定(阵元和子阵数固定)的情况下,寻找一组最优的子阵划分是一个难度很大的问题。它包含了极其广泛的搜索空间,导致运算量十分庞大。如即使将只有64个阵元的
矩形阵划分为8个子阵,就有约
种可能;更不用说包含几千个阵元的阵列。而且,阵列优化过程中还要满足众多的约束条件,这又大大增加了运算代价。对于子阵优化问题,传统的优化搜索算法难以胜任。
遗传算法是子阵优化的一种可行方案。遗传算法在解决大空间、非线性、全局寻优等复杂问题上具有很多优势,且有鲁棒性,对不规律的函数很有效且比其它优化方法具有更高的效率;具有既扩大搜索空间、又兼顾优化效率的优点 [5] 。
国内外对基于遗传算法的子阵划分问题进行了一定研究。文献 [6] 针对地震应用,对于阵元数20、阵元间距2.5 km的阵列,利用遗传算法优化子阵结构,使SNR提高了26%,但需要关闭一定数目的中心阵元;文献 [7] 对子阵结构和阵元加权同时优化,以抑制阵列方向图的旁瓣;但未考虑子阵级加权的情况,且对子阵结构和阵元加权同时优化会显著增加运算代价。文献 [8] 研究了差波束方向图的旁瓣抑制问题,给出了子阵结构和子阵加权的联合优化方案;但仅适用于线阵及对称划分的阵列,且只以阵元数100、子阵数4为例说明性能,阵列规模与实际情况有较大差距。
雷达系统中,抑制阵列方向图的旁瓣是一个基本问题;本文研究用于抑制方向图旁瓣的最优子阵划分方法。与文献 [7] 不同,本文阵元级采用Taylor加权,仅对子阵结构优化;且考虑了子阵级数字加权的情况。与子阵结构与阵元加权的联合优化相比,这种方案可降低运算代价和复杂度;且在不采用子阵级加权的情况下,可得到Taylor加权的旁瓣电平。
本文研究任意平面相控阵,并以阵元数1千左右、子阵数几十为例来说明优化结果,这与实际阵列规模比较接近。
子阵优化的运算量十分庞大,而且我们要求优化后的阵列为满布阵、各子阵均为非重叠子阵等,又大大增加了运算代价。如何提高遗传算法的收敛速度及运算效率,也是本文所要研究的一个重要问题。
2. 基于遗传算法的最优子阵划分
2.1. 遗传算法
为对相控阵的子阵结构进行优化,首要问题是选择一种高效的优化方法;显然应采用全局优化技术。模拟退火与其它进化方法可实现对设计空间的全局搜索,这其中就包括遗传算法。
遗传算法是基于达尔文进化理论的高效进化搜索方法,基本可解决所有优化问题,无论有无约束条件。其主要思想是从父代群体中保留好的个体,淘汰差的个体。它通过选择、交叉、变异等操作不断对个体进行优化 [5] 。遗传算法综合了定向与随机搜索的优点;尽管其是一种随机搜索方法,但与传统搜索方法不同,不依赖问题自身,可进行全局搜索,且搜索规模大、效率高,易于计算机实现。它是概率的不确定的状态转移,更容易得到全局最优解。遗传算法对搜索空间进行随机取样,与传统优化技术相比,其收敛到非全局最优解的可能性大大降低。
遗传算法是对大型相控阵进行子阵优化的一种有效方法。遗传算法在优化过程中利用适应度函数作为评价个体成功的测度。在对阵列特别是大型阵列进行优化的过程中,适应度函数是计算中最耗时的部分,因为它包含了对阵列方向图的合成与分析。
2.2. 目标函数
设阵列为由
个全向阵元组成的平面相控阵,位于xoy平面上,第1个阵元位于坐标原点,将其作为参考阵元,且设第
个阵元的坐标为
。阵元级采用Taylor加权,设第
个阵元的加权为
;通过移相器实现波束指向。用
表示仰角和方位角,设阵列波束指向为
。设阵列共被划分为
个子阵,且
为
的子阵形成矩阵 [2] [3] 。
令
,
,
,
,并设
(1)
则子阵转换矩阵可表示为
(2)
因而阵列的子阵级导向向量为
(3)
其中
为阵元级导向向量,且
。
设
为子阵级加权向量(用于进行数字处理),则以
为自变量的阵列方向性函数为
(4)
式中
表示Hadamard乘积, 表示共轭转置。
表示共轭转置。
本文中,遗传算法的目标函数即为方向图的旁瓣电平。
2.3. 子阵结构的编解码方法
为利用遗传算法对子阵结构进行优化,需要将阵列结构用二进制码表示,即将其映射为可由遗传算法计算的染色体编码形式。本文中,染色体的信息用于由阵列中的一个初始阵元生成一个子阵;解码染色体后,子阵被形成并更新状态标记,以表明在整个阵列中哪些阵元被划分到子阵内。
为此采用基于中心阵元的编码方法。其过程为:用一个随机的二进制串编码的染色体表示
个子阵中心的初始位置,其对应的阵元称为各子阵的中心阵元,并将该类染色体称为中心染色体。中心染色体的基因提供了中心阵元的信息,解码时它为一个包含所有中心阵元位置信息的向量。
中心阵元周围的阵元用另一类染色体、即周围染色体来表示。周围染色体包含了中心阵元周围的阵元中有哪些位于子阵内的信息。将周围染色体分为若干类。如第1类周围染色体为8位,用于表明紧邻中心阵元的8个阵元中有哪些位于该子阵内;图1为对其解码示意图。图中,阵元1、3、6、7 (用实心圆表示)位于该子阵内,在基因1中其相应位的代码为1;而阵元2、4、5、8(用空心圆表示)均不位于该子阵内,在基因1中其相应位的代码为0。类似地,第2类周围染色体的基因为16位,表明中心阵元周围第2层的16个阵元中有哪些位于该子阵内;而第3类周围染色体的基因为24位,用于表明中心阵元周围第3层的24个阵元中,有哪些位于该子阵内。
上述3类周围染色体表明了围绕中心阵元的48个阵元的子阵划分信息 [7] 。
2.4. 子阵划分的约束条件
为保证优化后的阵列性能,本文提出优化过程应满足的以下4个约束条件。
1) 解码后所有阵元均位于阵列的有效范围内
编码过程中,中心阵元是随机产生的,因而解码后的阵元可能位于实际的阵列范围之外。为避免出现这一情况,构造一个边界判断函数,在进行子阵划分后,利用该函数来判断是否有阵元超出阵列范围;如果有,则利用越界修正函数修正染色体中非法阵元所对应的基因位。
2) 同一子阵中所有的阵元相邻
子阵划分的基本要求是同一子阵中的所有阵元相邻。然而,基于中心阵元的编解码方法常常得到不相邻的子阵划分结果。为此设计相邻条件判断函数,同时构造一个数据链表并将满足条件的阵元放入到链表中。通过比较链表和解码后子阵中的阵元,将不在链表中(即不满足相邻条件)的阵元去除,从而实现了对非法阵元的修正。
3) 各子阵为非重叠子阵
我们要求各子阵为非重叠子阵,这在实际中更容易实现和控制。为此设置阵元状态标记位,在划分子阵后求出每个阵元的状态标记,再利用重叠阵元修正函数来去除重叠阵元(即同时位于不同子阵中的阵元)。
4) 阵列为满布阵
为使阵列得到尽可能的利用,要求其为满布阵,即所有阵元均被划分到某一子阵中。为此采用相邻插入的方法。首先求出阵列中每个阵元的状态标记位,对于未被利用的阵元,利用满布阵修正函数,按照相邻原则插入到已划分好的子阵中。
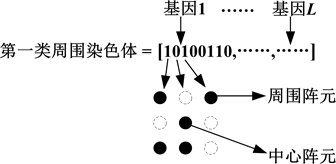
Figure 1. Schematic diagram of chromosome decoding
图1. 染色体解码示意图
3. 基于自适应交叉算子的改进遗传算法
利用遗传算法进行平面相控阵的子阵优化时,阵元数常常为数千,因而搜索空间十分巨大;而且又要满足众多约束条件,这又大大增加了运算代价。如何提高收敛速度及运算效率,是要解决的一个重要问题。
遗传算法中与收敛速度最相关的参数是交叉算子,其作用是组合交叉两个个体中有价值的信息以产生新的后代个体,使群体向优化的方向进化。本文对常规遗传算法进行改进,将常规算法中设定为常数的交叉算子
,修正为随目标函数值自适应变化的交叉算子
,并称其为自适应交叉算子。
自适应交叉算子定义为
(5)
式中,
为某一代目标函数的平均值,而
为其最优值。二者越接近则
越大,将在上一代选择更多的父代个体进行组合遗传,从而使子代的种群更为优化。
自适应交叉算子的引入使优化过程具有自适应交叉组合的特点,可较大提高收敛速度并改善运算效率。
4. 子阵划分流程
在实现了阵列结构的编码解码以及约束条件之后,基于改进遗传算法的子阵划分的流程为:
1) 随机产生中心染色体及周围染色体;
2) 对中心染色体和周围染色体解码,还原子阵结构;
3) 根据解码结果,判断是否满足约束条件,并修正染色体中的非法基因;即使同一子阵中所有阵元相邻,各子阵为非重叠子阵且阵列为满布阵;
4) 计算由解码得到的子阵结构所相应的方向图的旁瓣电平及适应度值;
5) 求出旁瓣电平的最优值及平均值,计算自适应交叉算子;
6) 分别对中心染色体和周围染色体进行选择、交叉及变异操作,以产生新的染色体;
7) 判断是否满足迭代次数,是则终止,否则返回2。
其具体流程图如图2所示。
5. 仿真结果
5.1. 仿真条件
以矩形平面阵为例给出仿真结果。设阵列中有
个全向阵元,按
间距的矩形栅格放置在xoy平面上。设阵列波束指向垂直于阵列平面。水平向(x轴方向)和垂直向(y轴方向)均采用−40 dB Taylor加权。设子阵个数为64。子阵级采用数字加权,用于超分辨空间谱估计等后续处理。
原始的子阵结构随机选取。遗传参数中,交叉概率自适应选取,变异概率为0.01,种群大小取为40,遗传代数取为50。
5.2. 改进遗传算法的收敛性能
图3给出了改进遗传算法与常规遗传算法收敛性能的比较。图中,纵坐标为每代40个种群解码所产生的子阵结构的方向图旁瓣电平的平均值。可见,改进方法的收敛性能明显优于常规方法:在同样的代数下可收敛到更优的结果。如经过50代遗传后,常规方法旁瓣电平的平均值收敛到−21.80 dB,而改进方法为−27.02 dB;其改善达5.22 dB,收敛性能得到显著提高。
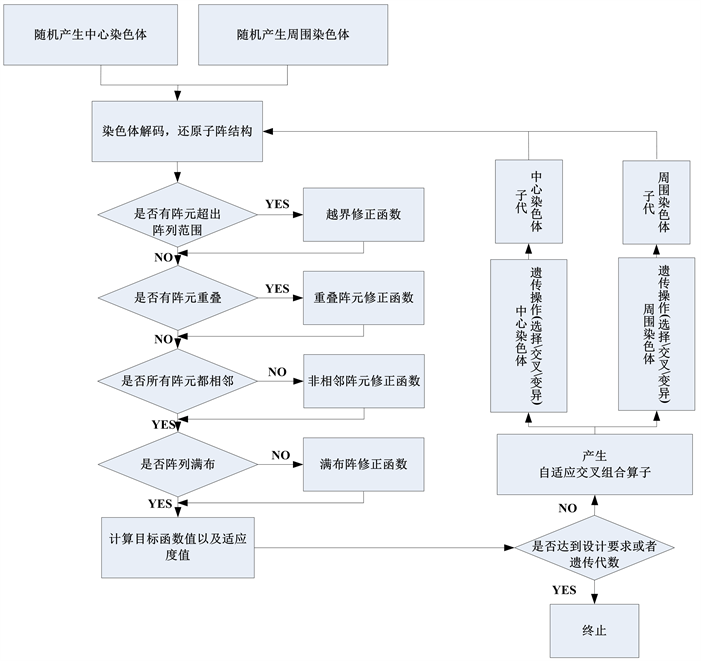
Figure 2. Sub array optimization flow chart based on Improved Genetic Algorithm
图2. 基于改进遗传算法的子阵优化流程图
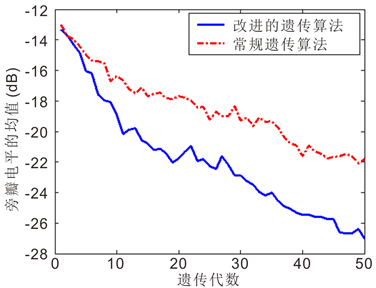
Figure 3. Comparison of convergence performance between the two methods
图3. 两种方法收敛性能的比较
5.3. 方向图
图4给出了利用改进遗传算法对子阵结构进行优化后,其阵列方向图在
的切面图;为便于比较,图中同时给出了原始子阵结构的方向图。可见,子阵优化后,方向图旁瓣电平得到了有效改善。图中原始和优化后的旁瓣分别为−8.82 dB和−29.44 dB,因而旁瓣改善20.62 dB,效果显著。
5.4. 子阵划分结果
图4给出了最优子阵划分结果,即图5中优化后的方向图所对应的阵列结构;图中用不同符号表示位于不同子阵内的阵元。
本文研究利用改进的遗传算法,对子阵进行优化,使优化过程具有自适应交叉组合的特点,改善了阵列方向图的旁瓣,与常规遗传算法相比可提高收敛速度及运算效率。同时由于基于中心阵元的子阵编解码方法在优化过程中可能产生大量不合理的子阵结构,利用约束条件进行判断和修正,但增加了运算代价及复杂度,研究提出了更高效的子阵编解码方法。