1. 引言
当前时代是航空产业高速发展的黄金期,在航空客运、货运和军事等相关行业出现井喷式的增长,迫切需要培养大量飞行员及其相关人才。然而,据国际民航组织的统计,仅由于气象原因造成的严重空中事故,就占民航总事故的10%~15%,与气象直接或间接有关的事故占民航总事故的三分之一左右。因此,加强危险气象条件下应对技能是飞行员必不可少的学习内容之一,迫切需要地面虚拟仿真软件在航空气象仿真上的支持。
低空风切变是指600米以下的空气运动在风向或风速上发生变化的一种自然现象,按照风速发生变化的方向,风切变分为水平风切变和垂直风切变两种。特别的垂直风切变对飞机起飞和降落阶段具有较大威胁 [1] 。微下击暴流是常见的一种垂直风切变现象,已经引起了多起空难事故。该气象条件发生时间短,强度大,预测困难,是航空领域头号“杀手”。
自上世纪八十年代起,众多学者试图对微下击暴流建立数值模型,研究其内在规律。Michael Ivan [2] 最早根据实测数据提出基于涡环的数学模型,其思想被后续学者所采用,进而提出更多改进模型 [3] [4] [5] [6] [7] 。由于经验模型与实测数据之间总存在一定差异,近代学者根据流体力学方程和微物理模型对微下击暴流进行数值仿真 [6] [8] [9] [10] [11] ,通过大量计算重现微下击暴流风场,取得了更高的仿真精度。
在面向地面飞行模拟训练 [12] [13] 的实际应用中,微下击暴流的仿真计算主要是为了向飞行员提供较为逼真的风切变气象条件的直观感受,训练飞行员在极端气象条件下的应对能力。这需要仿真软件能实时计算出飞机所在位置的风速和方向,并为飞行员提供可靠的感知反馈(包括视觉上风场提示和飞行姿态实时突变等)。现有微下击暴流仿真模型计算速度较慢,且不关注风场可视化技术,而传统流场可视化技术 [14] - [20] 在直观性和实时性上并不能满足飞行模拟软件的实际需求。
本文针对飞行模拟软件在飞行员风切变应变能力的培训需求,提出基于圆切线模型的微下击暴流实时仿真算法,并探索出一种基于粒子拖尾效果的风场可视化技术。实际测试表明,该方法能在不增加飞行模拟软件计算负担的前提下,实时为其提供微下击暴流的视觉效果和三维空间中任意位置的风场数据。
2. 微下击暴流仿真算法
下击暴流是一团强烈的局部下沉冷空气在近地面垂直运动而形成的特殊风场条件,其风速矢量在空中垂直与风向平面内发生急剧变化,对飞行器起飞和降落阶段的安全威胁较大。根据破坏性水平出流的尺度,下击暴流分为宏下击暴流(水平尺度超过10千米)和微下击暴流(最大出流水平尺度小于4公里)两类。由于微下击暴流出现频率高、隐蔽性强、危害大等原因,面向飞行模拟的下击暴流仿真研究主要针对微下击暴流现象。
现有微下击暴流仿真模型主要分为两类,基于涡环的数学模型 [2] 和基于流体力学的数值计算模型 [6] [8] [9] [10] [11] 。考虑到飞行模拟软件的实时性计算要求,本文采用基于涡环的数学模型方法更为合适,并在此基础上提出一种快速计算算法,可大幅提升其仿真风场的计算速度。
2.1. 基于涡环的数学模型
Michael Ivan [2] 最早根据气象观测数据提出基于涡环的微下击暴流仿真模型,其仿真结果与实测风场数据在视觉上具有较高的一致性,得到广泛应用。
将地面任意一点作为坐标原点,建立如图1的涡环模型。则地面上方 点的涡环曲线方程为:
点的涡环曲线方程为:
(1)
其中R是涡环的半径,流线方程为:
(2)
其中,
由涡环半径与预定风速
确定,
、
是仿真计算空间中当前位置
到主涡环的最大和最小距离,
为椭圆积分函数,
。
为使仿真风场在地面上的垂直风速为零,Michael Ivan模型使用第二个镜像涡环
(其中心位置
与主涡环中心位置
互为镜像),用于抵消地面位置的垂直风速。最终的仿真风场速度矢量为这两个涡环方程的诱导速度场:
(3)

Figure 1. The sketch illustration of the vortex ring model
图1. 涡环模型几何解释图
其中
。
Michael Ivan模型在计算上存在较大复杂度,对特殊位置(如主涡环自身和涡环中轴线等)存在奇异性问题,需要追加计算步骤。虽然后续研究者不断提出改进方案,但在计算速度上和程序复杂度上效果并不理想。
进一步,Michael Ivan模型计算出的仿真风场是严格轴对称的,与实际风场情况存在一定偏差,缺乏可调参数控制风场形状,不利于实际工程应用。
2.2. 本文圆切线模型
本节针对Michael Ivan模型存在的问题,提出一种新的快速计算方法,可支持更多形状调整参数。
Michael Ivan模型采用涡环的主要原因是微下击暴流表现出典型的涡流现象,即风场存在一个旋转中心点,而方程(2)的切线方向与涡流现象吻合。方程(2)及其切线防线的计算复杂性是Michael Ivan模型复杂度的主要来源,本节提出使用圆切线的方式大幅降低模型复杂度。
由于微下击暴流具有明显的轴对称特点,故无需在3D空间建立仿真模型,仅需在2D平面计算,然后按照中轴线旋转360度即可形成3D风场。将地平线视为x轴,垂直地面方向视为y轴,如图2建立模型坐标系,并设置两个风场涡环中心
和
,涡环半径分别为
和
。
Michael Ivan模型中计算涡环切线的过程,可以由图2中圆切线近似逼近,即风场在任意一点P的风矢量的方向与圆切线一致,大小与圆心距离调整:
(4)
其中
为尺度函数,可使仿真风速在距涡环中心R处达到极大值,并在涡环中心风速

Figure 2. The sketch illustration of the circle’s tangent model
图2. 基于圆切线的微下击暴流仿真模型几何示意图
为零。
为预定风速,代表微下击暴流的整体强度。为保证近地风速垂直风速为零,本节模型同样采用Michael Ivan的方式,即在地平线下放置两个虚拟涡环。
与Michael Ivan模型(3)相比,本节模型的计算仅涉及向量间计算,具有明显的计算复杂度优势且无需复杂的特殊位置处理过程。进一步,本节模型具有多个可调参数
,可灵活控制仿真微下击暴流的左右风场形状、涡环大小和风场卷曲形状,更利于工程实际应用。
3. 基于粒子系统的风场可视化技术
风场可视化是科学数据可视化中一个经典且有挑战性的研究方向,具有广泛的应用。与传统风场可视化研究问题有所不同,面向飞行模拟的微下击暴流仿真研究需要为飞行员提供一个直观的风场特性,而不是具体流场数据属性。传统基于图标或者线性积分卷积的方法绘制速度缓慢,绘图结果不适合飞行员视角的直观需求,并不能直接应用。
本节基于粒子系统及拖尾技术,提出一种直观的风场可视化算法,可在飞行模拟软件中实时提供风场视觉效果。
3.1. 粒子系统
在计算机图形技术中,粒子系统用于表现火、爆炸、烟、水流、火花、落叶、云、雾、雪、尘等自然现象,已经成为众多游戏引擎的必备模块。使用粒子系统作为飞行模拟软件中的风场可视化技术,可直接调用现有引擎模块,不增加额外软件开发负担。
在粒子系统中,每一个粒子都是独立实体,具有各自的属性(位置、速度、形状、颜色、透明度、生命周期等)。粒子系统负责实时更新每个粒子的属性,并根据其材质绘制相应图形。
本文算法仅关注粒子的位置属性,故假设粒子系统中所有粒子激活的粒子集合为:
(5)
粒子在风场的位置更新由下述方程控制:
(6)
其中
表示风场在
处的速度x分量,
是更新时间间隔。方程(6)本质上表示粒子在风场中是无质量的质点,按照风速流动,与流线的定义相一致。粒子系统负责将生命值
小于零的粒子清除,并在随机位置生成新粒子,从而实现粒子的动态更新过程。
原始粒子系统并不能直接表现出风场的外观,而传统可视化方案里给粒子施加箭头形状等的方式不适合飞行员观察风的流向。本文作者经过多种尝试,探索出粒子系统结合拖尾的新表现方式,形成近似“流线”效果,可快速绘制风场形状。特别的,由于并没有直接采用复杂的流线计算,本节算法对计算量的需求与传统粒子系统保持一致。
3.2. 拖尾技术
粒子运动轨迹与流场中流线的定义一致,可揭示出风场内部特征。由于粒子绘制结果偏小,其运动过程也较快,飞行员并不能有效观察到粒子运动轨迹。
借鉴流线的思想,本节提出拖尾技术,直接绘制每个粒子的运动轨迹,从而形成较为直观的风场特征。拖尾技术本质上是一组跟随粒子运动的多边形,其顶点随着粒子运动而动态更新。
设拖尾多边形顶点为
,图形引擎可根据这组顶点绘制一个条状多边形(如图3所示)。拖尾效果的实现仅需动态调整顶点位置即可:
(7)
由于拖尾技术仅是增加一个多边形的绘制,其计算速度远远高于流线计算和线性积分卷积计算。
4. 仿真实验结果
本文仿真硬件平台为一台PC计算机(Intel I7 CPU,16 GB内存,NVidia GeForceGTX770 GPU),在Unity引擎平台上,使用C#编程语言开发仿真软件。使用Unity自带Profile工具测试结果显示,本文仿真及可视化算法在每一帧生成过程中仅占4ms左右的时间,对飞行模拟软件的实时性几乎没有造成任何负担。
在相同涡环半径、涡环中心位置等参数的设定情况下,Michael Ivan模型产生的仿真与本文基于圆切线模型产生的仿真风场实验结果对比如图4。本文方法基本保持了与Michael Ivan模型的一致性,只是在微下击暴流外侧的风场风速有些偏大。对于面向飞行模拟器软件中训练飞行员对微下击暴流直观认知的应用而言,这种误差是可以接受的。
与Michael Ivan模型不同,本文提出得基于圆切线模型的仿真风场具有较多灵活的可调参数,可以生成种类多样的仿真风场(如图5),更加利于工程应用中根据实际需要调整风场形状。
对于计算产生的仿真风场,传统可视化技术(如图6、图7、图8)偏重让研究人员观察风场内部结构属性,且计算复杂而耗时,不能直接应用于飞行模拟软件中。
为了让飞行员更加直观的认识到微下击暴流的特性,本文提出的基于粒子拖尾的可视化技术可以动

Figure 3. Description of trailing algorithm
图3. 拖尾技术示意图
 (a) Michael Ivan模型仿真风场
(a) Michael Ivan模型仿真风场 (b) 本文方法仿真风场
(b) 本文方法仿真风场
Figure 4. Comparison of the simulated wind field
图4. 仿真风场实验结果对比图
 (a) 参数设置一
(a) 参数设置一 (b) 参数设置二
(b) 参数设置二 (c) 参数设置三
(c) 参数设置三
Figure 5. Simulated wind field under different parameter settings
图5. 本文算法在不同参数设置下的仿真风场实验结果

Figure 6. Visualization results by traditional graph-based method
图6. 传统基于图标的风场可视化结果

Figure 7. Visualization results by traditional stream-line-based method
图7. 传统基于流线的风场可视化结果
态展示风速、风向,更加具有直观性(如图9)。
为更加清楚的显示出本文基于粒子拖尾方法的效果,图10给出了对一个拖尾进行高亮的实验结果。该图中,白色高亮轨迹即为拖尾多边形
,坐标系(红绿蓝箭头)位置为拖尾多边形首顶点
(粒子点)位置。另外,本文方法可将粒子渲染成雪花、灰尘或者雨滴等自然元素,更加增强飞行员视觉体验。
本文可视化算法可直接应用到三维空间(如图11、图12和图13),并根据实际用调整拖尾的材质,在飞行模拟软件中灵活应用。
本文可视化方案采用多边形拖尾的技术,其的材质可以通过GPU上的着色器实时改变,从而为风场
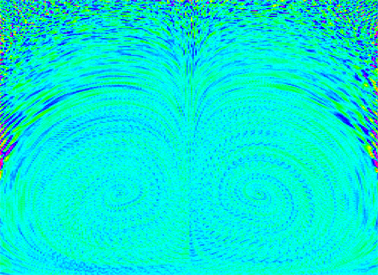
Figure 8. Visualization results by traditional convolution-based method
图8. 基于线性积分卷积的风场可视化结果

Figure 9. Visualization results by our trail-based method
图9. 基于粒子拖尾的风场可视化结果

Figure 11. Visualization results in a real 3D scene I
图11. 三维场景中的可视化效果(一)

Figure 12. Visualization results in a real 3D scene II
图12. 三维场景中的可视化效果(二)

Figure 13. Visualization results in a real 3D scene III
图13. 三维场景中的可视化效果(三)
可视化提供了多种方案的选择(如图14和图15,采用纯色或热折射效果),便于飞行模拟训练内容的灵活设置。
5. 结论
本文针对飞行模拟软件所需的气象条件视觉仿真问题,提出基于圆切线模型的微下击暴流仿真算法,并通过粒子系统和拖尾效果进行风场的实时可视化绘制。该方法具有简单易行、计算快速和画面视觉逼

Figure 14. A simulated and visualizated Microburst in a flight simulation scene
图14. 微下击暴流仿真效果及其在实时飞行模拟软件中的可视化效果

Figure 15. Visualization results by the heat distortion trails
图15. 采用热折射拖尾的可视化效果1
真度较高等特点,可在普通PC平台上实现微下击暴流的动态视觉仿真,具有实际工程应用价值。
与基于流体力学的专业级仿真方法相比,本文方法在风场物理特性精度方面具有一定差距。本文作者将继续研究带有物体特性仿真的风场建模方法,以便进一步提高气象条件的物理逼真度。
基金项目
国家科技支撑计划课题(2015BAH54F01)、江苏省自然科学基金(BK20141113, BK20130158)。
NOTES
1请查看在线视频,其动态效果更佳直观。https://www.bilibili.com/video/av31249132/。