1. 引言
大数据时代背景下,信息量爆炸式增长、传播速度日益加快,数据驱动的决策在日常生活中随处可见。房地产市场作为我国经济的重要组成部分,对其研究一直是学术界和实业界的热点问题。
在房地产价格的预测中,传统的时间序列仅考虑自身趋势,与房地产市场多因素影响、非线性波动的特点存在偏差;基于多因素指标构建的机器学习预测模型被应用到房地产价格的预测中。章伟(2011) [1] 提出一种粗糙集BP神经网络并验证了其在房地产价格预测中的有效性。刘彩云(2017) [2] 年提出基于多因素影响的组合预测模型,利用马尔科夫修正了小波神经网络的预测结果。Del Giudice (2017) [3] 利用遗传算法解释了那不勒斯中心地区房地产租赁价格与地理位置之间的关系,并通过与多元回归分析的比较验证了遗传算法的有效性。Bae (2018) [4] 在稳定的市场与受到结构变化与外部冲击的市场环境中分别验证了支持向量机、随机森林等机器学习方法,表明在房地产预测的准确性方面机器学习算法要优于传统时间序列模型。机器学习方法在房地产价格预测中的应用主要采用同频数据为影响变量,很少纳入混频数据指标。
而随着网络的普及和用户量的指数式增长,网络搜索数据开始成为建立预测模型的重要影响指标,Ginsberg (2009) [5] 等最早利用谷歌搜索数据对流感疾病趋势进行了成功预测。Askitas (2009) [6] 等通过研究关键词的搜索数据,相较于官方数据提前做出了失业率的预测。在国内应用网络搜索数据的研究也日益增多。董倩(2014) [7] 等利用网络搜索数据,采用交叉验证技术比较了不同的预测模型,证明了网络搜索数据在国内房地产价格预测中的有效性。孟雪井(2016) [8] 结合文本分析得到网络搜索关键词,接着利用时差相关系数法与随机森林进行筛选过滤得到符合我国投资者情绪的关键词词库,并以此构建了沪市投资者情绪指数。在房地产市场中,网络搜索指数的变化更有时效性,且可以在一定程度上体现供求双方的预期心理和行为情况。但是在现有的研究中,并未考虑到网络搜索数据与房地产指数间存在的频率差问题。而混频数据模型的应用则可以更大程度地利用数据样本的原始信息,提升预测可信度。
Ghysels (2004) [9] 等提出了混频数据抽样方法(MIDAS),通过构建MIDAS模型可以实现对不同频率数据的处理,利用权重多项式对不同滞后期的变量系数进行描述和刻画解决了之前存在的“维数灾难”问题。Pan (2017) [10] 等提出多输出混频支持向量机模型,利用低频数据实现对高频房地产及股票市场数据的预测,相较单输出SVM提升了模型的预测准确率。刘金全(2010) [11] 基于MIDAS模型实证研究证明了混频宏观数据在经济应用中的有效性。
本文在基本混频数据抽样模型的基础上,不同于传统的非线性最小二乘估计,采用全局寻优的粒子群算法获取模型参数,利用相关关键词的百度指数数据进行预测,相较官方数据的发布时间,预测结果可以提前进行预报。同时,在以往的研究基础上,选择新的常用影响指标,提出基于随机森林重要性排序和封装排序的特征选择算法,并将筛选后的组合变量与混频数据预测模型的拟合结果进行结合,使新的影响指标体系不仅囊括传统统计指标,也包含了网络搜索数据。在各类机器学习算法中,支持向量机同时考虑结构化风险最小与经验风险最小,且处理小样本、非线性特征问题十分优秀 [12] ,因此选择其作为修正模型,且针对其存在的参数难以确定、核函数选择无理论支持的问题,建立了混合核函数以实现局部与全局核函数的综合利用,且利用了PSO算法进行参数全局寻优。基于改进的支持向量机模型可以实现对混频数据抽样模型预测结果的修正,本文实现了模型时效性与精准性的综合提升。
2. 模型构建
2.1. 模型基础
首先,价格由供求关系决定,房地产具备投资品与消费品的双重特征,所受到的影响因素众多,且对其价格预测具有混沌性和非线性。其次,作为国民经济的重要组成部分,国家政府相关政策的制定对于房地产市场的影响也十分强烈。然后,房地产价格的预测在时效性的要求上较高,网络搜索数据能够在一定程度上体现房地产市场热度。最后,房地产市场还与其自身所处环境、土地开发状况以及各类配套设施的建设有着密切关系。综合来看,房地产市场的价格走势存在一定的规律性,但要对其进行准确分析与预测,单一使用房地产自身走势作为影响因素进行的时间序列预测,涵盖的要素过少,预测结果缺乏信服力,为提升预测结果可靠性,需要考虑更多的影响因素指标和更优秀的预测模型。
2.2. 模型步骤
1) 利用网络爬虫工具,根据定性分析以及百度推荐工具,获取影响房地产市场的相关百度指数数据指标,并基于AIC准则对相关指标进行逐步回归,选取最重要的前五个影响指标。
2) 选择从2011年1月至2018年1月的百度搜索数据以及国房景气指数作为研究对象,利用PSO-MIDAS单变量模型以及PSO-M-MIDAS多变量模型分别对百度指数与国房景气指数进行拟合,得到初始预测结果。
3) 选取房地产市场上下游的多个影响指标,构建指标体系,同时将国房景气指数进行趋势处理,分为上升趋势和下降趋势,构建随机森林为基础的封装特征选择模型,选取对房地产市场而言最为重要的影响因素作为输入变量。
4) 建立PSO-M-SVR模型,利用粒子群算法优化支持向量机相关参数,将混频抽样数据模型预测结果结合筛选指标作为输入变量,对初始预测结果进行修正,提高预测精度,并降低误差波动性。
2.3. PSO-M-MIDAS(m, k)模型
MIDAS模型区别于分布滞后多项模型的最重要性质,是其对于混频数据具有拟合预测能力,同时参数估计结果、模型预测精度均优于分布滞后模型。MIDAS模型在金融波动预测以及宏观经济预测等方面都有着广泛的应用,并取得了不错的预测效果。
Ghysels (2004)提出的MIDAS(m, k)模型包括参数化的多项式权重
,可以将高频数据
与低频数据
间建立回归联系:
(1)
模型当中,m表示的是数据之间的频率倍差,多项式权重的具体表达为
,
是高频数据的滞后阶数。常用的多项式权重函数包括Almon多项式函数,指数Almon多项式函数,β多项式函数,三种权重函数虽然表达方式不同,但都能够确保所使用的高频率滞后阶数的权重函数为正,同时多项式权重函数的表达式中实际包含了各项权重之和为1的前提条件。本文选择两参数的指数Almon多项式函数作为参数化权重函数,同时为了保证权重为正,方程误差小以及对应权重递减的特性,给定参数约束条件
。两参数的指数Almon多项式函数的具体表达式为:
(2)
Ghysels (2004)提出的多元混频预测模型M-MIDAS(m, K)基于单变量混频预测模型,任何一个经济系统都是一个复杂性系统,要想获得更为准确的预测效果需要利用多个解释变量的信息。M-MIDAS(m, K)模型的具体表达式为:
(3)
模型中n表示有n个解释变量。
多元混频预测模型相较单变量混频预测模型需要估计的参数更多,每增加一个变量就需要多估计一组(β, θ)值。
刘汉(2011) [13] 基于非线性最小二乘估计进行混频预测模型相关参数的估计,并用最大似然估计值作为评判依据,考察模型的有效性。本文结合粒子群算法(PSO)的全局寻优能力,以及自适应粒子变异性,实现混频预测模型的参数寻优。需要考虑更多的影响因素指标和更优秀的预测模型。
2.4. 基于随机森林的封装特征选择
房地产市场属于混沌的、非线性的经济市场,为了提升模型预测准确率,需要进行变量的重要度筛选。在传统的研究中,相关系数、卡方检验等 [14] 常被用来判定变量之间的相关性,考虑到本文具体涉及的房地产市场,文章采用基于决策树的集成模型——随机森林算法实现对特征的综合排序及封装排序。
2.4.1. 基于随机森林的特征值重要性综合排序
文章通过计算特征的gini值来对每个特征进行评价,gini指数的表达式为:
(4)
其中,
表示将特征m逐个对节点计算gini值变化量中类别K所占的比例,k则表示分类结果中的类别数。
Gini指数的变化量表示了特征j在相关节点上的重要性,具体表达式为:
(5)
其中,
和
表示的是对节点m进行分枝操作后的两个新节点上的gini指数。
如果特征J在决策树i中出现的节点在集合M中,那么特征j在第i棵树上的重要性则为:
(6)
由于随机森林是由n棵决策树集成的一种集成算法,因此需要综合考虑在n棵树上的所有重要性,表达式为:
(7)
在得到每个特征在所有决策树上的重要度之后,只需对其进行归一化处理,就可以得到所有特征值的综合排序情况。
2.4.2. 基于随机森林的封装特征选择
通过随机森林算法,可以得到每个特征值的综合重要性排序,但一般情况下,并不是选取排名靠前的几个变量就能获得最优的预测准确度。因此,在综合排序的基础上,文章进一步提出了封装特征选择的方法。
考虑到数据样本规模较小,因此选择10折交叉验证,用于提升模型可靠性与准确性。算法步骤如下:
1) 设置迭代最大次数
。
2) 给定需要排序的特征变量组合,将数据集随机分为十等份。
3) 在处理完成的数据集上生成随机森林训练模型,初步进行模型训练,在测试集上得到初始局部分类准确率
,初始局部平均分类准确率
。
4) 进行迭代运算,在测试集上得到每次的局部分类准确率
,并对
进行迭代更新,若
,则
。
5) 若
,则迭代结束,否则返回第二步。
6) 得到同一组变量组合的最优平均预测准确度,并得到该组变量集合的特征综合重要性排序结果。因为是采用10折交叉验证,因此,特征j的重要性值为
。
表示第j个特征在交叉验证第i组数据中的重要性值,进行降序排列。
7) 根据序列后向搜索方法,删除排名最低的特征值,形成的特征变量组合,并判断特征变量组合中的变量个数是否大于1,若大于1,则返回第一步。
8) 得到全局最优的分类准确率
,返回其对应的特征重要性排序结果。
算法流程图如图1所示。
2.5. 粒子群优化多核支持向量机预测模型
利用多元混频数据预测模型可以实现对原始混频数据的充分利用,在不损失数据原始信息的基础上实现预测。利用混频数据预测模型,获取了百度指数所包含的即时性,将预测结果作为间接影响指标,结合特征筛选过后的变量组合,实现对房地产市场的进一步非线性拟合。
支持向量机的泛化能力强,训练精度高,适用于小样本问题,且能解决线性不可分的问题,同时相较于BP神经网络模型有着不易于陷入局部极值点的优势。针对支持向量机存在的核函数选取无理论支持等问题,本文参照孙菲艳(2016) [15] 提出的改进支持向量机模型,构建新的混合核函数,实现支持向量机全局核函数与局部核函数的优势互补。具体核函数的形式如下所示:
(8)
式中,
表示多项式核函数,
表示柯西核函数。为进一步解决参数无法确定的问题,文章采用粒子群优化算法(PSO)实现对支持向量机多项式核函数的d,柯西核函数的u,权重系数θ以及惩罚系数C

Figure 1. Package filtering based on random forest
图1. 基于随机森林的封装特征筛选
的全局寻优。
PSO-M-SVR具体算法流程图如图2所示。
3. 实证分析
3.1. 数据选取及变量说明
为了避免重大经济危机对房地产市场带来的扰动,同时考虑中国网络普及情况,解释变量选取时间段为2011年1月至2018年1月,被解释变量的选取时间段提前一期,即为2011年2月至2018年2月。
3.1.1. 被解释变量
被解释变量为国房景气指数,数据来源于前瞻数据库,是由中国国家统计局于1997年研制并建立,反映中国房地产业发展变化趋势和变化综合量化指标体系。通过对国房景气值的预测,可以为国家宏观调控提供预警机制,也可以为投资者选择投资机遇提供决策依据。
3.1.2. 混频预测模型解释变量
使用百度推荐功能,得到与房地产市场相关关键词,并根据定性分析与AIC准则对各个关键词进行逐步回归,最终确定了房价走势,公积金,房价利率,房产税,以及装修五个关键词,各指数指标均为日数据,由python编写的爬虫程序从百度指数官网获取。
百度搜索指数为日数据,而国房景气指数为月度数据,因此将频率倍差m设置为30,对超过30天
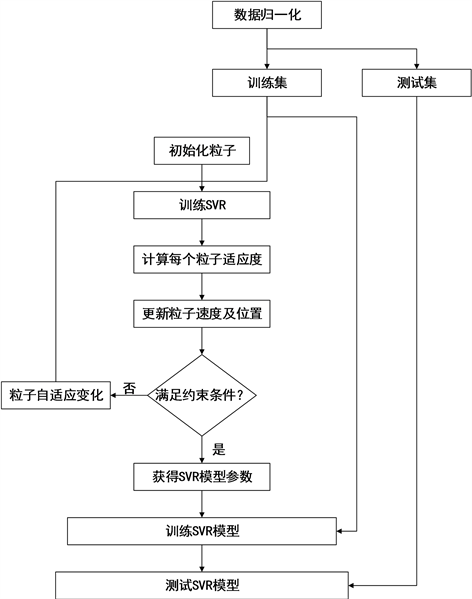
Figure 2. Algorithm flowchart of PSO-M-SVR
图2. PSO-M-SVR算法流程图
的月份进行数据删减,对2月份数据则结合1、3月份数据进行补充。同时,为了保证百度搜索指数的及时性与完整性,设置高频滞后阶数K为30。
3.1.3. 粒子群优化多核支持向量机模型解释变量
在现在研究的基础上,根据对房地产市场的综合分析及数据的可获得性,构建新的影响指标体系。将相关影响指标分为宏观影响因素、房地产企业上游影响因素、房地产企业自身影响因素、房地产企业下游影响因素以及被解释变量滞后自身因素五大类影响因素,每个影响因素均为月度数据,数据来源于wind数据库以及前瞻数据库。具体指标体系结构如图3所示。
3.2. 结果分析
3.2.1. 混频数据预测模型结果分析
利用2011年1月至2016年5月的数据作为训练集,利用粒子群优化算法分别对单变量混频数据预测模型与多元混频数据模型进行参数寻优,在2016年6月至2018年1月的测试集数据上进行预测结果观测。为比较混频数据预测模型结果优劣性,对百度指数数据进行加总平均处理,将频率为日度数据的百度指数指标转化为月度数据,并利用最小二乘回归进行数据拟合,得到同频预测结果,与多元混频数据预测模型及单变量混频数据预测模型预测结果进行比对。

Figure 3. Impact indicators of real estate market
图3. 房地产市场影响指标体系
选取反应预测相对误差的绝对误差AE、反应预测平均误差的MAPE以及反应误差波动性的RMSE作为评价指标,若MAPE值越小,则说明预测结果更准确;若RMSE值越小,则说明预测结果的误差波动越小。各指标计算公式如下:
(9)
(10)

Table 1. Prediction results of multivariate and univariate MIDAS models
表1. 多变量及单变量混频数据抽样模型预测结果
从表1数据可以看出,多元混频数据预测模型结果最优,但从预测结果来看,残差区间较大,各混频预测模型结果趋势预测仍有修正的空间,但相比同频化处理后的数据预测模型,已有了明显的改进,也表明了改进的混频预测模型利用了更多的数据样本信息。
3.2.2. 基于随机森林的特征选择结果
对被解释变量进行预处理,将上升趋势设为1、下降趋势设为0,视为二分类问题,计算每个解释变量对被解释变量的重要性程度。采用十折交叉验证,对于构建的影响房地产市场的指标体系进行基于随机森林的初始重要性综合排序(按降序排列)为:国房景气指数滞后一阶;货币供应量(M1);房地产开发投资完成额;全国建材家居景气指数(BHI);消费者信心指数;土地购置费;商品房销售额;工业增加值增长;土地购置面积;房地产新开工施工面积;外汇贷款数据;采购经理指数(PMI);房地产竣工面积;社会消费品零售总额;房地产施工面积;工业品出厂价格(PPI);房地产开发企业资金来源;居民消费价格指数(CPI),而封装特征选择的结果则为:国房景气指数滞后一阶;货币供应量(M1);房地产开发投资完成额;全国建材家居景气指数(BHI);消费者信心指数;土地购置费;商品房销售额;土地购置面积;房地产新开发施工面积;房地产竣工面积。
3.2.3. 基于粒子群优化多核支持向量机模型预测结果分析
为了判断SVM是否对多元混频数据抽样模型达到了修正的效果,建立四组模型,模型一、模型二、模型三、模型四分别表示将封装筛选后的特征变量组合、将加总平均换成月度数据的百度搜索指数、将筛选后的特征变量组合与多元混频数据预测模型预测结果进行整合以及将筛选后的特征变量组合与加总平均变换的百度搜索指数整合作为输入变量的预测模型。模型三即为对利用支持向量机模型对混频率数据抽样模型的修正。
将整体样本划分为训练集与测试集,训练集样本时间跨度为:2011年2月至2016年5月;训练集样本时间跨度为:2016年7月至2018年2月,样本选择时间区间均为被解释变量时间跨度。在训练集上优化参数并构建预测模型,在测试集上对模型结果进行观测。各模型预测结果如下:
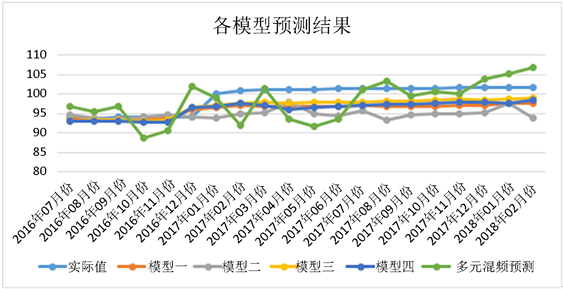
Figure 4. Prediction results of different models
图4. 各模型预测结果
从各模型预测拟合结果图4可以看出,模型二,即选用加总的百度搜索指数作为输入变量波动性较大,与原始值的走势存在偏差;而其它模型均与原始值的走势基本一致。
选取除MAPE、RMSE之外,新增绝对误差AE作为评判模型预测优劣性的依据。AE计算公式为:
(11)
其中,Prevalue表示预测值,Actvalue表示实际值,n表示预测值数量。
从表2数据可以看出,模型三与模型四的预测结果相较于模型一与模型二要更好,表明在封装筛选后的特征变量组合中加入百度搜索指数指标提升了预测模型的预测准确度,同时降低了预测误差波动。且模型三取得了最佳预测精度与最小的误差波动率,即结合多元混频数据预测模型拟合结果的预测模型表现最好,利用多元混频数据预测模型PSO-M-MIDAS与PSO-M-SVR的组合预测能有效提高预测的准确度、修正了多元混频数据预测模型的预测结果,使预测结果能够更加准确地的与实际数据走势相稳合,通过实证分析证明了本文建立的模型能对我国的房地产市场进行更加有效更加快速的预测。
4. 结论与展望
由于数据统计的原因,各类数据指标通常存在频率差,传统的同频化处理会损失数据样本的原始信

Table 2. Prediction results of optimization and comparison models
表2. 优化及对比模型预测结果
息,而混频数据抽样模型可以提升数据样本的利用率,从而达到提高预测准确度的作用。
本文在算法上实现了对混频抽样数据及支持向量机的优化,使用粒子群算法优化的混频数据抽样模型,且根据随机森林的特性提出了一种有效的特征筛选方法,在此基础上利用混合核函数及优化参数的支持向量机回归模型对混频数据模型预测结果进行修正;在指标体系的构建上综合利用了百度搜索指数与传统房地产市场影响指标。实证证明了本文提出的预测模型在房地产市场上的有效性,利用SVM对混频数据抽样模型结果的修正从预测准确性及趋势稳合度方面都达到了预期要求。
随着时代的发展和数据可获得性的不断增强,以后研究面临的数据类型越来越丰富,不仅需要考虑更多有用的数据指标,且需要提出适应能力更强的算法模型,这也是文章需要继续研究的方向。
致谢
感谢对本文进行写作、修改及投稿建议的导师肖智老师,您以渊博的知识和理论体系提出的每条真知灼见都令我如醍醐灌顶一般,感谢为本文提出修改意见和各位师兄师姐、师弟师妹,感谢女朋友一如既往的陪伴与支持。