1. 引言
反馈现象源自于电子放大电路的“反馈”概念,主要是指信号经过放大电路时,输出信号回授至输入端时所引起的输出信号加强(正反馈)或减弱(负反馈)现象。目前有关反馈现象的研究,除去电子放大电路之外,还常见于系统动力学的基本理论研究 [1] 。但有关负反馈方程的研究仅局限于电子线路中的放大器,并且多以实验性测试而进行的定性或半定量分析为主 [2] ,缺少具体的反馈机制性的研究。反馈机制的复杂程度是显而易见的,本文所要讨论的是反馈现象中的负反馈现象,并且仅限于反馈因子是线性的线性负反馈。
在电子放大电路中,负反馈是通过反馈信号使得净输入量减小,从而提高增益的稳定性,减小非线性失真 [3] 。许多现象表明,负反馈在系统从平衡态被破坏到新平衡态建立过程中,同样起着重要的作用,在诸如燃烧、落体运动、LR电路等系统中都有负反馈现象发生。
本文旨在建立一类线性负反馈的数学模型,完整反映封闭系统中相关物理量变化的规律。
2. 线性负反馈问题
2.1. 燃烧现象中的负反馈
我们观察到,在一个封闭系统中,燃烧生成物CO2气体对燃烧的进程会有阻碍作用。由反应方程式C + O2 = CO2知,随着CO2气体浓度的升高,O2的浓度在下降,因它们的浓度变化比例相同。由燃烧规律,设CO2气体浓度的变化率和O2浓度成正比,且O2起始浓度为
,产生的CO2气体浓度为
,则有
,其中k为比例系数。
即
(1)
分离变量并积分有
得
即
(其中
) (2)
将初始条件
代入(2)式,得
。于是所求CO2浓度的解为
(3)
由(3)式可以看出,随着时间t的增加,CO2气体浓度
逐渐接近于常数
,且不会超过O2的开始浓度
,CO2达到一定浓度,燃烧就会停止。
2.2. 自由落体中的负反馈
在物体自由下落过程中,我们注意到,随着物体速度的增大,物体所受空气阻力也会增大,最终速度趋于稳定值,冰雹、雨滴的运动都是这样的。
现有质量为m的物体在空气中自由下落,若物体所受空气阻力与速度成正比,根据牛顿第二定律,有
(4)
注意到
,易知方程(4)的解 [4] 为
(5)
从(5)式可以看出,随着时间t的增加,物体下落的速度逐渐接近于常数
,最后物体的运动趋于匀速下降。
2.3. LR电路中的负反馈
当线圈中的电流变化时,它所激发的磁场通过线圈自身的磁通量也在变化 [5] ,线圈自身通过产生感应电动势来减弱这一变化。法拉第电磁感应定律就是对这一负反馈现象的描述。
如图1所示,电阻R和电感L都是常量(电感L的电阻不计),当开关S闭合时,电路中的电流开始
增加。由法拉第电磁感应定律知,当电流i变化时,L上有感应电动势
。由回路电压定律可得
(6)
注意到
,解方程(6)可得
(7)
从(7)式看出,随着时间t的增大,电路中电流i逐渐稳定于常数 。
。
3. 线性负反馈数学模型
3.1. 模型的建立
从式(1)、(4)、(6)式看出,在线性负反馈中,都有一个稳定的诱导量I (如以上各式中的
、
和
),反馈量kf (如上述各式中的
、
和
),以及内禀常数m (如以上(4)、(6)式中的m,L,(1)式中的常数为1)。由此,负反馈标准方程可经验地表示为
(8)
这个方程的一个特解是
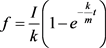 (9)
(9)
3.2. 模型讨论及意义
3.2.1. 负反馈方程的性质
负反馈方程(8)是具有线性反馈因子kf的一阶微分方程。“负反馈”概念虽然来自于电子放大电路,很明显,本文所建立的负反馈方程远远超出了电子放大器所研究的范围,其意义更广,范围也更大。需要说明的是,相比于那些非线性反馈因子kf n (n > 1),本文所讨论的线性负反馈是最简单的一种类型。在涉及速度负反馈问题中,指的是低速反馈现象 [6] 。
由于负反馈方程(8)中的相关物理量在不同事件中的意义不同,所以说负反馈方程式(8),更多意义上表达的是,不同负反馈现象中相关因素的一种结构关系。在诸多负反馈现象中,凡反馈方程可以表达成形如式(8)的,说明他们都有相同的反馈结构。对于同一反馈类型,反馈因子k是相同的常数。但在不同形式的反馈中,常数k又是不同的,它的大小由具体的反馈实验测量而得。
3.2.2. 负反馈方程的意义
1) 系统从一个平衡态到另一个平衡态发展的过程中,负反馈方程
能帮助我们清楚这一演变的过程。在燃烧现象中,一个封闭系统,燃烧生成物CO2气体浓度的增加,是由碳在氧气中燃烧导致的,但随着CO2气体浓度的增加,又对燃烧的进程起阻碍作用。当CO2气体达到一定浓度时,燃烧就会停止,系统进入平衡态;在自由落体现象中,物体速度的增加是由重力引起的,但随着物体速度的增大,物体所受空气阻力也会增大,当阻力和重力平衡时,速度就趋于稳定值;同样,在LR电路中,感应电流i是由电动势E引起的,但随着电流i的产生,电感线圈中就会出现反向的感应电动势,这个感应的电动势削减了E的作用。由此看出,诱导量I促使物理量f的产生,但通过反馈因子k又对物理量f的产生起到抑制作用,保持了系统状态的相对稳定性。
2) 物体质量是物体惯性大小的量度,这一论断在负反馈方程的解
中得到了明确的、强有力的理论说明:内禀常数m的大小,决定了系统在诱导量I的作用下,重新达到稳定性的快慢。常数m越大,系统到达新平衡态越迟,体现的是系统保持原有状态不变的性质,即物体的惯性。
LR电路中的电感系数L,和内禀常数m相比,同样起到延缓电流i增长的作用。
3) 在负反馈方程中,当诱导量I消失后,方程就和法拉第电磁感应定律方程形式相同,意义也相同。反馈系数k的符号,对应的是楞次定律的思想。当环境中反馈因子不存在时,方程就和牛顿第二定律形式相同。
4) 在封闭系统内,反馈系数k削减了诱导量I的作用,最终使f稳定在
的大小。和内禀常数m相
比,k是由系统内环境因素决定的。内禀常数m和反馈系数k,反映了在系统演化过程中,当一个平衡态被破坏后,在到达新的平衡态前,系统对自身稳定性的维持(通过m体现)和对环境适应性调整(通过k体现)的规律性。
5) 线性负反馈模型可以为更加复杂的非线性负反馈研究提供理论基础。
4. 结论
在系统平衡态演变过程中,存在负反馈现象。负反馈不但延缓了系统到达新平衡态的时间,同时也影响着系统新平衡态的状态。对于一些简单的系统,其平衡态演变过程可以用简化的数学模型表达出来。
参考文献