1. 引言
基金公司从成立以来,作为专业的投资机构总能被市场关注。基金的持股情况更是一直广泛受到投资者的关注。由于基金仓位数据公布比较少,一般只会在每一季度结束后才会公布当季基金仓位,所以存在一定的滞后性。对投资者来说,仓位数据无法作为判断市场情绪的参考。因此,如果能提前给出基金仓位的测算,投资者就能做出更好的投资决策。
国外对于基金仓位问题的研究比较早,比如投资组合理论 [1] ,资本资产定价模型 [2] 、Fama五因子模型 [3] 。目前,国内杨艳军 [4] 通过行业因子收益和规模因子收益对基金的收益进行了解释,使用多因素优化方法建立了基金仓位配置模型。何青峰 [5] 通过最优化法,选取了行业因子和规模因子对基金收益进行绩效分。马永谙 [6] 认为国内的基金仓位估算模型已经经历了四个阶段,对比分析了每一代模型在算法上和误差上的不同之处,并认为,通过引入神经网络、因子分析、最优化等方法,基金仓位测算的精准性会逐步提高,模型将更加完善。海琴 [7] 运用BP神经网络构建基金仓位的测算模型,选取单只基金“华夏成长证券投资基金”收益率时间序列作为研究数据,证实了模型的有效性。曲荣华 [8] 为了解决指数间的共线性问题,对每个指数分别进行简单线性回归得到各自的系数,再通过最优化处理得到系数前的比重,最后对各系数按比重加权求和得到仓位估计值。目前已有的研究主要是通过最优化法来解决变量间的多重共线性的问题,本文在二次规划法的基础上引入逐步回归法和Lasso回归法,通过剔除有共线性影响的变量来实现对基金仓位更准确的测算。
2. 数据及符号说明
2.1. 数据说明
本文的数据来源于wind金融终端。选择投资类型为普通股票型和偏股混合型的基金,时间为2018年1月1日到2018年12月31日,剔除2018年之后成立的基金以及正处于清盘期或者建仓期的基金。根据获取的2018年四个季度的基金净值数据计算日收益率作为因变量,根据四个季度的中信29个一级行业指数每个交易日的收盘价数据计算日收益率作为自变量,通过建立变量间的回归模型实现对基金仓位的测算。
2.2. 符号说明
表1给出了本文涉及到的相关符号的解释说明。
3. 多元线性回归模型
以基金的日收益率作为因变量,分别对中信一级行业指数以季度为周期进行回归,模型为:
对得到的系数
进行求和即为测算的基金仓位。这里多元线性回归模型是作为下面要介绍的二次规划、逐步回归和Lasso回归这三种模型的理论基础。
4. 二次规划
二次规划模型可以通过多元线性回归模型转化得到,它的本质就是带约束的线性回归。优化目标是使回归模型的均方误差最小。即
由于基金投资于单个指数的股票资产比例是在(0,1)之间,并且证监会对公募基金仓位有一定的范围限制,因此可以得出系数的约束条件,如下所示:
分别对每只基金进行二次规划模拟系数,并计算每只基金对应模型的R2值。选择R2大于0.5的模型对系数进行求和,得到对应基金的仓位值。图1和图2分别给出了用二次规划法测算的偏股混合型和普通股票型的基金仓位与季报公布的实际基金仓位值的误差分布。
从四个季度仓位测算的误差分布来看,二次规划法测算的误差大部分分布在(5%, 15%)区间。因为基金仓位在短时间内变动本身不会太大,所以如果模型测算的误差达到5%以上说明测算效果不好。
从结果来看,由于二次规划法在测算系数时没有考虑自变量的多重共线性(即行业指数间的多重共线性),所以产生了较大误差。图3是中信29个一级行业指数间的相关系数热图:

Figure 1. Error distribution of partial-equity hybrid funds
图1. 偏股混合型基金误差分布

Figure 2. Error distribution of common stock funds
图2. 普通股票型基金误差分布
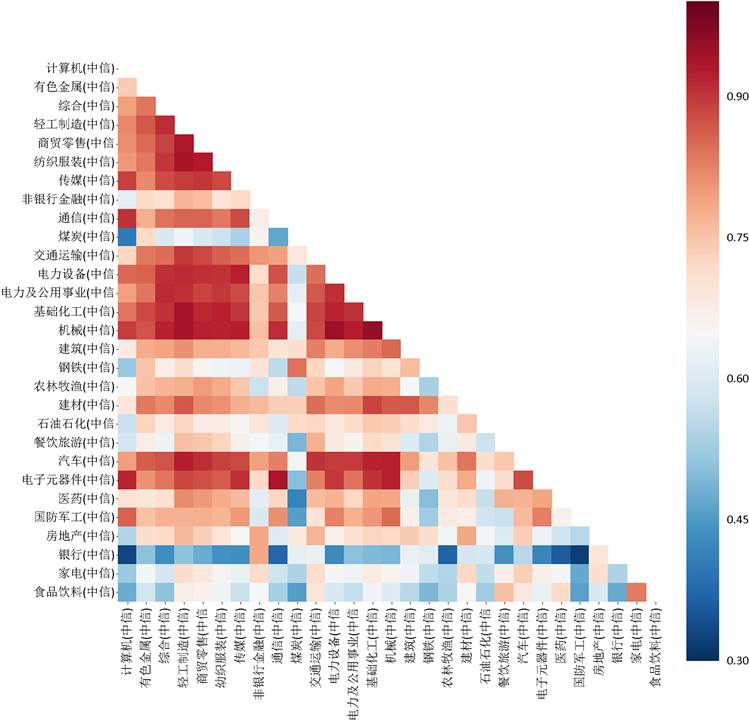
Figure 3. Relevance coefficient of industry index
图3. 行业指数相关系数
从图3中可以看出行业指数之间存在较大的相关性,所以对仓位进行测算时需要解决多重共线性的问题,因此在二次规划法的模型基础上引入了改进的模型。
5. 改进的模型
为了降低行业指数之间的多重共线性,下面采用逐步回归法和Lasso回归法来拟合基金日收益率与行业指数日涨跌幅之间的回归模型。
5.1. 逐步回归
逐步回归基本思想是有进有出,每次引入或剔除自变量,都对原模型和新模型进行F检验。如果新自变量的引入能够显著提升模型的解释能力,那么引入该自变量;如果原自变量的剔除不会显著降低模型的解释能力,那么剔除该自变量。直到不再有变量被选入或剔除为止,保证最后所得的回归子集是最优子集。通过对行业指数与单只基金的相关系数从大到小排序,依次引入模型。当p值小于0.05则保留变量,否则剔除该变量。
在逐步回归的过程中,逐渐剔除掉共线性较强的成份(行业指数),保留相对独立的成份,假设基金只在这些成份上进行配置,将这些成份的回归系数加总得到基金仓位预测值。
逐步回归的模型得到的R2值均大于0.9,保留下来的变量系数也通过显著性检验。图1和图2分别给出了用逐步回归法测算的偏股混合型基金和普通股票型基金误差的分布。可以看出此方法下模型误差在(−5%, 5%)区间的数量增加,而在(5%, 15%)区间的误差数量明显减少,说明逐步回归的结果相对于二次规划法的结果误差小。
表2给出易方达国防军工这只基金通过逐步回归法得到的系数值,可以看出该基金在国防军工行业上的投资占比明显大于其他行业,属于行业配置较为集中的基金。因此用逐步回归法测算的结果比较符合实际,但对于行业配置比较分散的基金则估计效果就不太理想。
5.2. Lasso回归
Lasso回归是引入L1正则化项的线性回归,是多元线性回归的有偏估计,适用于共线性数据,它可以通过将系数进行压缩直到零从而达到剔除部分自变量的目的。Lasso回归的结果对正则化系数λ取值敏感。实际使用过程中,需要通过交叉验证的方法选择合适的λ值。
以K折交叉验证为例,将样本随机分成K份,每次取K-1份作为训练样本拟合Lasso回归模型,计算该模型在剩余1份验证样本的均方误差;重复K次,得到该模型在K组验证样本的均方误差均值。对一定范围内可能的λ值进行遍历,选择验证样本均方误差均值最小的λ值,作为最终的Lasso回归正则化系数。Lasso回归的损失函数为:
这里根据交叉验证结果得出惩罚系数λ = 0.1时Lasso回归得到的样本均方误差最小,且回归的R2值均在0.9以上。
图1和图2分别给出了用Lasso回归法测算的偏股混合型基金和普通股票型基金的误差分布。该模型得出的误差分布与逐步回归的误差分布相似,比二次规划法的误差小,说明这两种方法在此问题上得到的验证结果都优于二次规划法的结果。
图4和图5是根据对时间进行滚动得到的求和仓位再加权平均与实际平均仓位的对比图。因为基金仓位只在每一季度末的季报公布,所以2018年只有四个季度末的数据。

Figure 4. Position comparison of partial-equity hybrid funds
图4. 偏股混合型基金仓位对比

Figure 5. Position comparison of common stock funds
图5. 普通股票型基金仓位对比
图4和图5折线图与实际仓位值对比可以看出Lasso回归测算的基金的平均仓位非常接近真实值。
6. 模型结果对比
表3给出了这三种方法测算的平均仓位与实际四个季度报告公布的平均仓位的绝对误差数据,从表中可以看出逐步回归和Lasso回归的误差相比二次规划法的误差要小,误差基本都在0到5%之间。说明逐步回归和Lasso回归测算的结果对于判断市场基金平均仓位走势有比较大的参考价值。
综合来看,这三种方法都可以测算出公募基金的仓位。二次规划法可以得到基金在每个指数上的投资比例,但是这种方法面临的一个问题是自变量之间的多重共线性。逐步回归法通过逐步筛选变量能够降低多重共线性,它对于行业配置比较集中的基金的仓位的测算效果比较好,但是对于行业配置分散的基金仓位的测算效果就不太理想。Lasso回归通过对系数加入惩罚项,避免估计值过大影响效果,并且通

Table 3. Error comparison of average position
表3. 平均仓位误差对比
过绝对值压缩来剔除变量,降低多重共线性,但是这种方法剔除变量是完全基于数据的基础上进行的,并没有涉及单个基金实际持仓信息,从而有可能剔除关键变量。
这三种模型都是通过建立基金日收益率与指数日涨跌幅的回归模型,从而可以测算基金的仓位。从绝对误差角度来看,逐步回归和Lasso回归测算结果的误差比二次规划法测算的误差都小,所以如果想要估算单只基金的仓位变动情况或者预判整个后市的动向变化,采用逐步回归和Lasso回归效果会更好。当涉及行业配置比较集中的基金仓位的测算时,用逐步回归法得到的结果会更符合实际预期。对行业配置分散的基金进行仓位测算时可以用Lasso回归。
7. 结论
为了避免被投资者或者竞争者摸清自身的投资策略,基金经理可能会在季末进行临时调仓而达到“粉饰”季报的目的,或者基金经理更换人选导致投资风格大变都会影响模型的估计效果。但模型整体误差近似呈现正态分布,所以在计算平均误差的时候可以通过增加参与测算的基金的数量来降低误差。
目前已有的资料中关于基金仓位的研究比较少,原因在于基金净值和持仓相关的信息可获取的非常少,对于研究的开展比较困难。本文主要就是基于二次规划法、逐步回归以及Lasso回归这三种方法根据可获得的公募基金的净值数据来测算基金的仓位。根据仓位的变动趋势来判断后市动向从而作出相应的投资决策。在后续研究中,可以增加时间跨度、数据量,再结合基金持仓方面的信息进一步优化方法。