1. 引言
递归算法是一种直接或者间接地调用自身算法的过程,递归算法把大问题转化为规模缩小的同类问题的子问题,将一个复杂问题逐步简化并最终转化为一个最简单的问题,最简单问题的解决就意味着整个问题解决。递归算法对解决一大类问题是十分有效的,它往往使算法的描述简洁而且易于理解,为一些问题提供了最简单的解决方案 [1] 。递归算法简洁、规整,虽然在整体结构上易于理解,但在分析递归运行情况时,总给人不可捉摸、难以理解的感觉,主要原因是递归调用实现机制太抽象,递归函数层层跳转、回溯,使人们对递归算法的分析难以把握。
多年来,很多学者对递归算法的分析进行了深入研究,但还存在一些不足,文献 [2] [3] [4] 在讨论递归算法结果时,一般根据函数调用的过程直接分析,对于简单的问题容易实现,但对复杂递归函数分析就困难重重,分析过程过于抽象,极易出错;文献 [5] [6] 使用递推函数对递归算法分析研究,这种方法不具有通用性,而且一些递归算法难以转换为递推式;文献 [7] [8] [9] 提出了用递归树研究递归的方法,将递归与树进行映射,便于操作,但分析时局限于单棵树,注重于函数调用关系的研究,而递归调用中有时是多棵树组成的森林,递归树在处理这些问题时显得不足,且在树上标注,处理结构不清晰。
本文将森林引入递归算法的分析处理过程,解决递归算法分析中存在的问题,通过建立递归与森林的逻辑映射关系,根据对程序递归结构分析,判断树结构,由入口函数,建立搜索树,所建立的树不仅限于二叉树,根据实际问题可以是单分支树,可以是二叉树、多叉树,甚至多棵树,到达叶子节点进行回溯,将程序结构映射为森林,并根据执行情况建立状态调用表,既分析全面,又使分析结构清晰、结果准确,有效解决了递归算法结果分析中的难题。
2. 树在递归分析中的应用
递归算法整个过程分为两部分:递推和回归,递归调用由多个子递归构成,递归的结构和处理与树的特点很相似,树由多个子树构成,对树的遍历就是搜索和回溯的过程,所以在递归算法分析上可以将递归结构映射到树型结构上,可以用树结构进行递归算法的分析。实际问题中,存在一些分支语句中含有递归的情形,这时需要分成多棵树,多棵树组成逻辑上的森林。
森林为M棵互不相交的树的集合,表示为F = {T1, T2, ∙∙∙, Tm} [10] ,T1, T2, ∙∙∙, Tm为组成森林的树,可以将递归算法逻辑映射为森林,具体处理上以树为处理单元,建立标准的处理流程。
递归算法映射到树时,在分析中对树的遍历采用先根遍历,边界条件即为树的叶子节点,下面以一简单递归类型的程序结构为例,说明使用树对递归算法分析的过程,在第3部分采用具体实例进行详细说明:
(1)void Recursive (int m, int n)
{
(2) if (m==0)
(3) return ;
(4) if (n==0)
{
(5) a= Recursive (m-1,1);
(6) return a;
}
(7)else
{
(8) b= Recursive (m-1,n);
(9) printf(“%d %d”,m,n);
(10) c= Recursive (m,n-1);
}
}
2.1. 分析程序结构
首先分析程序的整体结构,函数Recursive为递归函数,作为树的基础节点,通过深度搜索对树节点进行扩展,每次递归函数执行过程的节点作为树的一个节点类型;其次要分析递归函数在程序结构中所处位置,语句(5)的递归函数与语句(8)、(10)的递归函数处于不同的语句结构体中,执行到语句(5)时程序跳转到另外一棵树,所以要分成两个不同的树进行处理,这两棵树构成森林;第三,语句(8)、(10)在一棵树中进行处理,处理过程扩展为二叉树,b和c处于二叉树的不同分支;第四,两个分支中的其他语句,如:程序中的处理语句(9)在b执行到叶子节点回溯到c的过程中执行。
程序中语句(2)、(4)为边界,搜索到叶子节点时执行,执行语句(4)时跳到另一棵树执行搜索;语句(1)为程序入口,可看作根节点。
2.2. 建立树型图
根据对程序结构的分析,明确树的总体结构,本示例为两棵树构成的森林,每棵树为二叉树,入口函数作为树的根节点,从根节点进行深度搜索,由搜索情况建立树节点,到叶子节点进行回溯。多棵树组成的森林,在搜索树节点时,根据实际情况进行树间跳转,根据搜索情况绘制树型图,标明节点序号。
2.3. 建立状态调用表
树只建立节点,根据节点扩展情况,对应树的节点建立对应状态调用表,调用表反映状态变化及其他语句块执行,一方面反映程序整体全貌,另一方面使分析更加清晰、直观;状态调用表主要内容有:节点编号、节点名、节点动作、节点值等,根据树的搜索情况建立该表,回溯节点前加H代表回溯动作,回溯到根节点,递归算法分析结束,结果为递归算法处理结果。
3. 实例分析
3.1. 汉诺塔问题
有A,B,C三根柱子,A柱上按大小顺序从下往上摞着n片圆盘,现在要将这些圆盘从A柱移至C柱,并保持上小下大的顺序。移动规则如下:每次只能移动一个盘,大盘不能放在小盘上。
程序主体结构:
void hanoi (int n,char a,char b,char c)
{
if(n==1)
{
printf(“%c-->%c”, a,c);//1
}
else
{
hanoi(n-1,a,c,b );
printf(“%c-->%c”, a,c);//2
hanoi(n-1,b,a,c);
}
}
递归分析:
将递归函数作为树的节点,程序中有两个递归函数分别为树的左右分支,左分支:hanoi(n-1,a,c,b),右分支:hanoi(n-1,b,a,c),其他处理语句单独列明:如:1语句在n等于1时执行,为出口语句,2语句在右分支前执行,在下述实例中只在4、5、7节点前执行。
假如初始调用为hanoi(3,'A','B','C'),则调用树结构如图1所示,执行过程调用状态如表1所示。
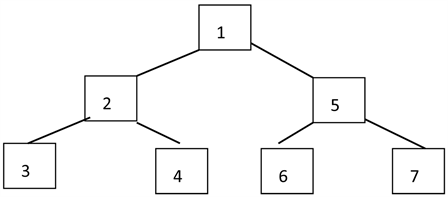
Figure 1. The tree structure of the Tower of Hanoi
图1. 汉诺塔执行的树结构


Table 1. The Tower of Hanoi call status table on execution procedure
表1. 汉诺塔执行过程调用状态表
3.2. 2018 noip普及组试题三(3)
int findans(int n,int m)
{
if(n==0) return m;
if(m==0) return n%3;
return findans(n-1,m)-findans(n,m-1)+findans(n-1,m-1);
}
将return findans(n-1,m)-findans(n,m-1)+findans(n-1,m-1),修改为:
f1= findans(n-1,m)
f2= findans(n,m-1)
f3= findans(n-1,m-1)
return f1-f2+f3
调用实例findans(1,2)
树为三叉树,第一分支为findans(n-1,m),第二分支为findans(n,m-1),第三分支为findans(n-1,m-1),函数简称为f(n,m)。
语句f1-f2+f3在第三分支后执行,return m,return n%3为出口语句。
调用树结构如图2所示,执行过程调用状态如表2所示。
结果为:3。
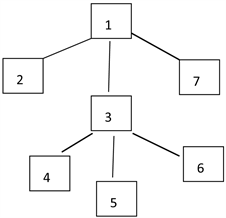
Figure 2. The tree structure of 2018 noip popularization group
图2. 2018 noip普及组树结构

Table 2. The call status table of 2018 noip popularization group
表2. 2018 noip普及组调用状态表
3.3. 阿克曼函数
阿克曼函数定义:
n+1m=0,n>0
A(m,n)=A(m-1,1) n=0,m>0
A(m-1,A(m,n-1)) n>0,m>0
程序主体结构:
int Ackerman(int m, int n)
{
if (m==0)
return n + 1;
if (n==0)
return Ackerman(m - 1, 1);
else
return Ackerman(m - 1,Ackerman(m, n - 1));
}
因为递归函数是参数,语句return Ackerman(m - 1,Ackerman(m, n - 1));修改为:
a= Ackerman(m, n - 1);
b= Ackerman(m - 1,a);
return b;
因为if语句含有递归函数,所以分为两棵树,树1称为t1,树2称为t2。t1有两个分支,左分支为Ackerman(m, n - 1),右分支为Ackerman(m - 1,a),函数简称为A(m,n)。t2有1个分支为Ackerman(m - 1, 1)。
入口调用函数为:A(1,2)
t1调用树结构如图3所示,执行过程调用状态如表3所示,跳转后的分支树t2的调用树结构如图4所示,执行过程调用状态如表4所示。
结果为:4。

Table 3. The call status table of T1
表3. T1树调用状态表

Table 4. The call status table of T2
表4. T2树调用状态表
4. 结论
当前对递归算法的分析方法主要有:根据函数调用的过程直接分析 [2] [3] [4] ,使用递推函数分析 [5] [6] ,这两种方法分析递归算法的局限性是显而易见的,在分析稍复杂的递归算法时是无能为力的;用递归树分析递归过程 [7] [8] [9] ,分析时局限于单棵树、状态调用过程不清晰;本文通过对递归不同类型典型实例的分析,将递归算法逻辑映射到森林,用树结构处理递归函数结果。给出了用森林分析递归函数的基本流程,通过分析程序结构、搜索建立分析树和状态变化对照表,到达叶子节点进行回溯,既分析全面,又使分析结构清晰、结果准确,有效解决了递归算法结果分析中的难题。