1. 引言
本文选取大学数学学习情况作为研究方向,探索其影响因素并据此给出行之有效的建议。多年来国内外学者从各个方面对数学学习质量进行研究分析,如彭乃霞、廖爽和陈亚萍 [1] 指出数学焦虑是影响大学生数学学习成绩的主要因素;陈玉文 [2] 指出非智力因素与大学生数学学习有显著的相关性;李红霞 [3] 指出高等数学自主学习情况与学生性别、年级、理论基础等因素有关;Weiss Iris R [4] 从教师授课的角度分析了不同因素对学生数学学习造成的影响。
论文主要从大学生学习态度及日常学习习惯的角度探寻影响数学学习质量的因素,向山东理工大学统计与数学学院的教授们获取专家意见,以山东理工大学财管、市销和金融本三个专业的学生为调查对象,设计问卷调查。最终共收回问卷308份,为保证问卷的完整性,采用有效问卷239份。
2. 基于AHP对大学生数学质量的影响因素的分析
2.1. 构建多层次结构模型
本文是从大学生学习态度及日常学习习惯的角度探寻影响数学学习质量A的因素,可将其划分为课前预习、课堂学习、课后学习和考前准备四大指标,并将各个指标细化为多个影响因素,形成层次影响因素结构
,见图1。
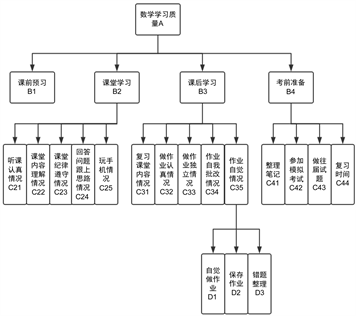
Figure 1. Hierarchical chart of influencing factors
图1. 影响因素层次结构图
2.2. 一致性检验并确定各影响因素的全局权重
建立递阶层次结构后,通过专家咨询得出各层的两两比较判断矩阵,并据此计算单层次排序。
采用和积法计算判断矩阵的最大特征根及其对应的特征向量,即解
,所求得W,经规一化处理后即为同一层次相应因素对于上一层次某因素相对重要性的排序权重。
各层次单排序计算及一致性检验结果如下:
判断矩阵
判断矩阵
,
,
判断矩阵
判断矩阵
,
,
判断矩阵
,
由计算结果可知,数学学习质量A、课堂学习情况
、课后学习情况
、考前准备情况
以及作业自觉情况
的判断矩阵都有满意的一致性,且课堂学习情况
、课后学习情况
都具有较好的一致性。
C层次总排序的一致性检验:
D层次总排序的一致性检验:
由计算结果可知,认为C层次总排序和D层次总排序的结果具有满意的一致性。因此,我们可以认为由上述判断矩阵计算出来的权重是可取的。通过对权重进行计算合成,可得到各影响因素的全局权重。大学生数学学习质量影响因素全局权重如表1所示。

Table 1. Each factor affects the weight
表1. 各影响因素权重
2.3. 各影响因素权重结果分析
基于影响指标权重的计算结果,我们可以看出一级影响因素中,课堂学习具有最高的全局权重约为0.4414,其次是考前准备(全局权重约为0.3134),再次是课后学习(全局权重约为0.1668),最后才是课前预习(全局权重约为0.0783)。课堂学习具有最高的全局权重充分说明了课堂学习质量的优劣是影响大学生数学学习质量的一个重要方面,因此学生要是想提高自身数学成绩,首先做好的就是课上认真听讲学习。
观察15项影响因素的权重,发现差别很大。其中课堂听课认真程度和课堂内容理解情况权重最高,作业自我批改情况权重最低,若再次细分,则保存作业情况所占全局权重为最低。在所有因素中,影响数学学习质量排在前6位的因素分别是:课堂听课认真程度、课堂内容理解情况、考前复试时间情况、回答问题跟上思路情况、整理笔记情况、课前预习情况。
3. AHP结合多元回归对影响大学生数学学习质量因素的实证分析
为寻找出参与调查的同学对影响数学学习质量的因素的看法,下面以成绩为自变量,各个影响因素为因变量建立回归模型。通过SPSS软件操作,模型建立如下:
:复习课堂内容情况;
:回答问题跟上思路情况;
:课前预习情况;
:考前学习时间。
由表2统计分析结果可知,进入模型的因素有复习课堂内容情况、回答问题跟上思路情况、课前预习情况和考前学习时间,且前两项因素是正向指标后两项因素是负向指标。综合同学们的情况来看,说明课上紧跟老师思路、课后及时复习巩固所学知识对数学学习有积极的影响。但课前预习和考前复习时间的影响并没有达到理想中的效果,这与层次分析法分析出来的结果有显著差异,尤其是考前复习时间的影响与之出入甚大。普遍而言,考前准备时间越充足,成绩一般越好,但这也只是相对的。平时认真学习的同学考前不需要花费过多的时间去复习,只需拿出是平时学习时间2倍左右的时间,而平时不主动学习的同学或许可以通过“考前突击”式的准备来提高成绩,但成绩不会随着复习准备时间直线上升。所以较长的准备时间并没有出现想象中的效果。观察排除的变量,听课认真程度与课堂内容理解程度对数学学习质量是有一定的正向影响,但由于二者的容忍度较小(0.464, 0.432),说明存在较强的多重共线性,加之在课上能回答问题跟上思路的学生,一般都会听课认真且能较好地理解课上学习内容,故将这两个因素排除在模型之外得到了解释。因此我们可以认为据专家意见计算出的影响因素权重是可取的。存在误差的原因还有一点,就是调查问卷的数据会出现不真实的情况。观察数据的拟合优度,发现数据拟合效果确实不好。
结合同学们的反映与层次分析法得出的结论再次建立回归模型,以成绩为因变量,以层次分析法得出的前六大影响因素为自变量。通过SPSS软件操作,建立模型如下:
:课堂内容当时理解程度;
:学习时间;
:课前预习情况;
:回答问题跟上思路。
由表3统计分析结果可知,模型中的课堂内容理解程度、回答问题跟上思路正向指标、考前学习时间和课前预习为负向指标。综合来看,课堂内容理解程度与回答问题跟上思路这两个因素占比最重,考前复习时间和课堂听课认真程度这两个因素都可得到合理的解释。对比上个模型,发现得出的结论相似。
4. 研究建议
综上,我们得知课堂学习与考前准备对数学学习有较强的影响。据此给出学习建议:适当做好课前预习;争取做到课上认真听讲、跟上老师思路,尽可能的在课上理解所学的知识。独立且及时地完成课后作业可以巩固所学的新知识以及检验自己的学习效果,如果有时间反思错题则学习效果会更好;考前将听讲笔记系统整理有助于梳理数学知识点,使之有一个明确的知识脉络,对相应内容有更加深入的理解。
参考文献
NOTES
*通讯作者。