1. 引言
探索性因子分析 [1] (EFA)是一系列用来发现一组变量的潜在结构的方法。它通过寻找一组更小的潜在的或者隐藏的结构来解释已观测到的、显式的变量间的关系。可以把繁杂的数据整理划分为多个维度,也可以解释问卷的结构效度。R软件完全免费,由新西兰Auckland大学的RobertGentleman和ROSSIhaka等研究开发 [2] 。其功能强大包括数据存储与处理、数组运算、统计分析、统计制图等,还可实现自定义编程。目前国内学者喜欢使用的SPSS软件需购买版权,随着整个社会越来越重视版权,使用未购买版权的SPSS软件分析而来的文章,刊发将会面临障碍,尤其是准备发表国外正规期刊时,R软件完全免费,不存在版权问题 [3] 。目前越来越多的科研工作者开始使用。
2. 探索性因子分析
2.1. 探索性因子分析模型 [4] (见图1)的一般表达形式为
其中,x表示观测变量,FM代表因子分析中最基本的公因子(Common factor),它们是各个观测变量所共有的因子,解释了变量之间的相关;U代表特殊因子(Unique factor)。它是每个观测变量所特有的因子,相当于多元回归分析中的残差项,表示该变量不能被公因子所解释的部分:wM代表因子负载(Factor-loading),它是每个变量在各公因子上的负载,相当于多元回归分析中的回归系数;而e则代表了每一观测变量的随机误差。
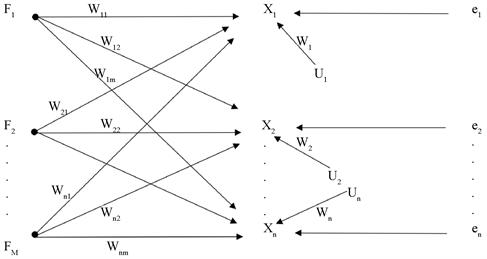
Figure 1. Exploratory factor analysis model (Source: Guo Zhigang [5] , 1999)
图1. 探索性因子分析模型(来源:郭志刚 [5] ,1999)
2.2. 探索性因子分析步骤
① 收集观测变量:通常采用抽样的方法,按照实际情况收集观测变量数据。② 构造相关矩阵:根据相关矩阵可以确定是否适合进行因子分析。③ 确定因子个数:可根据实际情况事先假定因子个数,也可以按照特征根大于1的准则或碎 石准则来确定因子个数。④ 提取因子:可以根据需要选择合适的因子提取方法,如主成分方法、加权最小平方法、极大似然法等。⑤ 因子旋转:由于初始因子综合性太强,难以找出实际意义,因此一般都需要对因子进行旋转(常用的旋转方法有正交旋转、斜交旋转等),以便于对因子结构进行合理解释。⑥ 解释因子结构:可以根据实际情况及负载大小对因子进行具体解释。⑦ 计算因子得分:可以利用公共因子来做进一步的研究,如聚类分析、评价等 [6] 。
3. 对象和方法
3.1. 对象
本次研究以昆明医科大学护理学院护生为对象。纳入标准为实习过两个月以上的实习护生,愿意填写问卷的护生。
3.1.1. 护生对伦理学知识应用效果问卷
使用自制问卷进行调查。该问卷包含22条目,问卷中对问卷进行初步的划分维度,均采用Iikert5级计分法。随机抽取70名学生进行调查,最终回收问卷70份,有效问卷65份。
3.1.2. 问卷的内部一致性检验
采用克朗巴哈α系数评估问卷的内部一致性。用R软件分析,问卷本次调查的克朗巴哈α系数为0.802,说明问卷具有较高信度。适合做探索性因子分析。
3.2. 方法
3.2.1. 导入数据及数据预处理
① 将65份的数据用EpiData软件录入后导出为sav文件。② 将数据命名为X123456.sav。③ 打开R studio软件,点击import Dataset,选择从SPSS中导入数据。
输入>library(psych)#载入psych包
cor<-cor(X123456)#计算变量相关系数矩阵并赋值给cor。
其中相关系数矩阵的原理,其是由矩阵各列间的相关系数构成的。也就是说,相关矩阵第i行第j列的元素是原矩阵第i列和第j列的相关系数。
3.2.2. 判断需要提取的公共因子数
fa.parallel(cor,n.obs=65,n.iter=100,fa=fa,show.legend=FALSE,main=scree plot with parallel analysis)#n.obs:样本量cor:相关系数矩阵;#fa = fa,因子分析;#n.iter:模拟分析的次数;#main:标题命名。运行代码后得到碎石图:
分析:图2中,实线表示真实数据,虚线表示模拟数据。
因子分析(FA)即三角形线,通过模拟,真实数据中只有4个主成分高于模拟数据;Kaiser-Harris 准则,在探索性因子分析中,Kaiser-Harris 准则的特征值取值应该是大于0,而不是主成分分析中的大于1,这是大多数人所不了解的。根据图形,我们可以看出有7个公共因子特征值大于0;Cattell 碎石检验,通过绘制特征值与公共因子数的图形,因此我们选择7个公共因子。当然在选择公共因子时,有时候我们也可以我们所需要的公共因子数,来进行调整。需要考虑到因子分析中的累计方差贡献率。
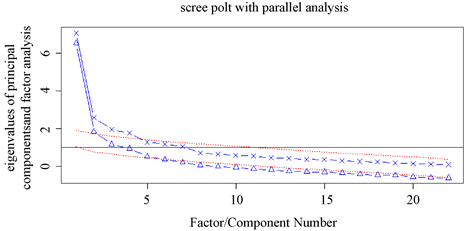
Figure 2. Parallel analysis of gravel maps
图2. 平行分析碎石图
3.2.3. 提取公共因子
fa<-fa(correlations,nfactors=7,rotate=none,fm=pa)
#r:相关系数矩阵;#nfactors:设定公共因子数;#rotate:指定旋转方法。
代码运行后,输出结果如下:
PA1 PA2 PA3 PA4 PA5 PA6PA7
SS loadings 6.78 2.22 1.60 1.380.88 0.74 0.56
Proportion Var 0.31 0.100.07 0.06 0.040.030.03
Cumulative Var 0.310.41 0.48 0.540.590.62 0.64
已删除了多余的输出
其中,SS loadings行包含了与公共因子相关联的特征值,指的是与特定公共因子相关联的标准化后的方差值,Proportion Var行表示的是每个公共因子对整个数据集的解释程度,Cumulative Var行表示累计的公共因子的累计解释程度。
可以看到,在提取公共因子中,原始数据中的特征值和方差贡献率分别为:① 特征值:第1公共因子特征值为6.78,第2公共因子特征值为2.22,.....省略.....第6公共因子特征值为0.74,第7公共因子特征值为0.56;②方差贡献率:第1公共因子解释了问卷中31%的方差,第2公共因子解释了10%,.....省略.....第6公共因子解释了3%,第7公共因子解释了3%。累计共解释了64%的方差。累计方差贡献率大于64%,说明在提取公共因子中的因子分析是可靠的。
3.2.4. 因子旋转
fa.varimax<-fa(correlations,nfactors=7,rotate=varimax,fm=pa)#使用正交旋转来计算。varimax表示最大方差旋转法。pa表示主轴迭代法。
代码运行后,输出结果如下:
PA1 PA2 PA3 PA5 PA6 PA4 PA7
SS loadings 4.65 3.031.62 1.51 1.16 1.10 1.10
Proportion Var 0.210.14 0.07 0.07 0.05 0.05 0.05
Cumulative Var 0.21 0.35 0.42 0.49 0.54 0.59 0.64
已删除了多余的输出
可以看到,在提取公共因子中,旋转后的特征值和方差贡献率分别为:① 特征值:第1公共因子特征值为4.65,第2公共因子特征值为3.03,.....省略.....第6公共因子特征值为1.10,第7公共因子特征值为1.10;② 方差贡献率:第1公共因子解释了问卷中21%的方差,第2公共因子解释了14%,.....省略.....第6公共因子解释了5%,第7公共因子解释了5%。累计共解释了64%的方差。
在经过了因子旋转后,特征值和各公共因子贡献率发生了变化。
3.2.5. 获取因子得分
scores<-fa(correlations,nfactors=7,rotate=varimax,fm=pa,scores=TRUE)#Scores:设定是否需要计算因子得分。
3.2.6. 因子分析可视化
fa.diagram(fa.varimax,simple=TRUE,digits=3)#digits=3表示保留3位小数。
> corrplot(fa.varimax$loadings)

Figure 3. Factor analysis visualization (factor score)
图3. 因子分析可视化(因子得分)

Figure 4. Factor analysis visualization
图4. 因子分析可视化
4. 结果
4.1. 根据图3、图4得出旋转后的因子得分
公共因子PA1中q11:0.813、q12:0.774、q8:0.761、q7:0.760、q10:0.743、q6:0.705、q14:0.629、q9:0.569;在公共因子PA2中q1:0.794、q2:0.777、q3:0.763、q5:0.724;在公共因子PA3中q20:0.776、q16:0.603;在公共因子PA5中q21:0.752、q22:0.066;在公共因子PA6中q18:0.747、q17:0.608;在公共因子PA4中q15:0.716、q13:0.567;在公共因子PA7中q19:0.751、q4:0.497。
4.2. 根据图3所示,提取出公共因子
包括:PA1:人文关怀和有利原则因子;PA2:基础护理因子;PA3:慎独因子;PA5:护患沟通因子;PA6:保密原则因子;PA4:护理决策因子;PA7:执行医嘱和医疗监督因子。利用探索性因子分析出来的结果与原先问卷中构建的问卷模型基本相符,说明问卷的结构效度良好,可以进行下一步分析。而且使用R软件可以方便的用因子分析法对实际的问题进行计算。
5. 结论
在此次研究中,R软件可以以清晰的碎石图(图2),向我们展现出清晰的数据,其中根据图形,我们可以看出有7个公共因子特征值大于0;Cattell碎石检验,通过绘制特征值与公共因子数的图形,因此我们选择PA1:人文关怀和有利原则因子;PA2:基础护理因子;PA3:慎独因子;PA5:护患沟通因子;PA6:保密原则因子;PA4:护理决策因子;PA7:执行医嘱和医疗监督因子。当然我们也可以从提取公共因子中应用简单的程序得出,这里采用了主轴迭代法,当然也可以灵活地应用最大似然法(ml)、最小二乘法(wls)等,得出每个公共因子的特征值及方差贡献率,在因子旋转部分选用正交旋转中最常用的最大方差旋转法来实现。可以明显地看出,与因子旋转之前的结果相比,在人文关怀和有利原则因子中,方差贡献率减少了;慎独因子的方差贡献率没变;基础护理因子、护患沟通因子、保密原则因子、护理决策因子、执行医嘱和医疗监督因子的方差贡献率都增加了。然而,在R软件中,还可以对数据进行可视化及显示各公共因子的因子得分(如图3)情况。由此可以看出R软件是一款免费开放且方便的软件,而且应用R软件可以方便而且快捷地用因子分析方法对实际问题进行分析计算(图4),检验问卷的结构效度。有利于下一步科研工作的进行。
NOTES
*通讯作者。