1. 引言
近年来,基于实际需求和理论研究,约束控制系统的设计在国内外开始盛行并备受关注,包括对系统的输入 [1] 、输出 [2] 和状态 [3] 等方面的约束,如果在系统运行过程中违反约束控制条件,则会影响系统动态性能,致使系统不稳定,更有甚者会损坏物理器件,有时需要人工干预来满足约束条件,这样既耗时又耗力。一般而言,针对具有输入约束 [1] 的控制系统,主要是通过死区输入、饱和输入和迟滞输入等几种方式来对系统进行约束。同时,针对具有输出和状态约束的控制系统方法 [3] 也相继问世,其中包括模型预测控制方法(MPC)、超驰控制、不变域控制法、自适应变结构控制、误差转换函数、极值搜索控制、饱和补偿方控制方法和障碍李雅普诺夫函数控制方法等。本文采用正切型障碍李雅普诺夫函数控制方法进行约束控制。
基于障碍李雅普诺夫函数的自适应约束控制方法能在不需要得到系统显式解的情况下使得约束条件不被违反,因而,与后期调试或试凑相比,该方法的可操作性更高,特别是针对高阶非线性系统或者大规模互联过程。目前正切型障碍李雅普诺夫函数得到了较为广泛的应用。在文献 [4] 中,针对一类具有参数不确定和全状态约束的严格反馈非线性系统,基于所构造的调节函数,提出了一种正切型障碍李亚普诺夫函数来保证跟踪误差的有界性,结合一个数值算例,证明了该方法能够达到预期的性能,且不突破全状态约束。而在文献 [5] 中,则是利用障碍李亚普诺夫函数对具有输出约束的严格反馈非线性系统进行系统化的控制设计,提出了基于对称和非对称对数型障碍李亚普诺夫函数的反推控制设计方法,保证了输出约束条件不违反,并证明闭环系统中的信号有界性。通过仿真,对比了正切型障碍李亚普诺夫函数和对数型障碍李亚普诺夫函数来说明控制性能的差异。在文献 [6] 中,针对具有状态约束的多输入多输出(MIMO)非线性系统,提出了一种新的自适应容错控制(FTC)方案,构建了一种新的正切型时变障碍李亚普诺夫函数,设计了一个辅助系统来分析输入约束的影响,在两自由度机械手控制系统上,验证了该方案的有效性。
本文针对具有全状态约束和输入饱和的非线性单输入单输出系统进行自适应跟踪控制研究。利用反步递推和神经网络逼近相结合的方法设计了自适应控制器。利用误差函数得到了一个连续可导的非对称饱和模型,再通过构造恰当的正切型障碍李雅普诺夫函数来解决约束控制问题,保证了系统所有状态均不违反约束条件,其中tan-BLFs可以同时处理具有约束和无约束的系统,证明了闭环系统的所有信号都是一致最终有界的,误差信号收敛到零的小邻域内。最后,通过仿真例子进一步验证了所提约束控制策略的有效性。
2. 问题描述及稳定性分析
2.1. 系统描述
考虑下面一类非线性严格反馈系统
(1)
其中,
是系统的状态,且
,
是一个常数;
是系统的输出,
是不确定非线性光滑函数,
是已知函数。
为饱和器的输出,也是系统的输入,
是饱和器的输入,有如下描述
(2)
其中,
,这里
和
是分别是执行器的上界和下界,
和
分别是标准符号函数和高斯误差函数。
为了便于接下来的控制器设计,定义如下函数

其中,c为正常数,u和v均为时间函数。则
(3)
将公式(3)代入系统(1),可得
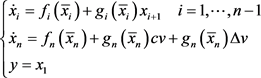 (4)
(4)
对于系统(4),现提出如下假设、引理及注解。
假设1:
是一个连续有界函数,因此
和
都可导。
假设2:假设对于
,
满足
,同时i阶时间导数
满足
,其中,
是正常数,
。
假设3:信号的控制增益函数
是已知的,存在常数
使得
。
假设4:存在常数
,
和
,使得
和c在系统(1)中满足
,
。
引理1:对于有界的初始条件,如果存在一个连续和正定的李雅普诺夫函
,满足
,这样就有
,其中
,
是
类函数,并且
是一个小的正常数,那么结果就是
是一致有界的。
本文的控制目标是构造一个自适应神经网络控制器,使系统输出y能较好的跟踪上期望信号
,并且全部的状态都不违反约束界,所有信号是半全局最终有界的。
2.2. 控制器设计和系统稳定性分析
本节运用反步递推方法对具有输入饱和全状态约束的非线性严格反馈系统进行神经网络自适应控制器u的设计,最终证明系统是稳定的。现给出误差变量
和虚拟控制器
的定义,即
,
,
第1步:定义误差变量
,
,并且选取正切型障碍李雅普诺夫函数
,其中
,
是正常数。根据系统(4)、公式(2)和公式(3),则有
(5)
对时间t求导,则得到
的表示如下
(6)
利用神经网络逼近
,则有
(7)
其中,
是神经网络权重向量,
是神经网络逼近误差,
,
。将式(7)代入式(6),可得
(8)
根据杨氏不等式有
(9)
取
,记
,其中
,且
是
的估计,将(9)代入(8)有
(10)
设计虚拟控制器
如下
(11)
其中,
是正设计参数,且
,将虚拟控制器(11)代入(10)得
(12)
第2步:定义误差变量
,
,并且选取正切型障碍李雅普诺夫函数
,其中
,
是正常数。则根据系统(4),式(11)得到
(13)
其中, ,且
,
对时间t求导,再将(13)代入,则
表示如下
,且
,
对时间t求导,再将(13)代入,则
表示如下
(14)
利用神经网络逼近
,则有
(15)
其中,
,将(15)代入(14)有
(16)
根据杨氏不等式,有
 (17)
(17)
取 ,记
,其中
,且
是
的估计(17)代入(16)得
,记
,其中
,且
是
的估计(17)代入(16)得
(18)
设计虚拟控制器
如下
(19)
其中,
是正设计参数,且
,将虚拟控制器(19)代入(18)有
(20)
第i步
:定义误差变量
,
,并且选取正切型障碍李雅普诺夫函数
,其中
,
是正常数。则根据系统(4),得到
(21)
其中,
,并且有
接着,
对时间t求导,再将(21)代入,则
表示如下
(22)
利用神经网络逼近
,则有
(23)
其中,
,将(23)代入到(22)得到
(24)
根据杨氏不等式,有
(25)
取
,记 ,其中
,且
是
的估计,再将(25)代入(24)得到
,其中
,且
是
的估计,再将(25)代入(24)得到
(26)
设计虚拟控制器
如下
(27)
且有
,根据(13)和(21),再将虚拟控制器(27)代入到(26)得到
(28)
第n步:定义跟踪误差变量
,其中
,
是正常数。则根据系统(4),得到
(29)
其中,
,并且
选取正切型障碍李雅普诺夫函数
(30)
其中,
是正设计参数。
对时间t求导,再将(29)代入,则
表示如下
(31)
利用神经网络逼近
,则有
(32)
其中,
,将(32)代入到(31),得到
(33)
根据杨氏不等式有
(34)
将(34)代入到(33)得到
(35)
现取函数v如下
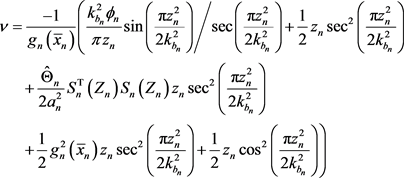 (36)
(36)
根据(12)、(20)和(30),将函数v代入,得到
(37)
设计如下自适应律
(38)
其中,
为修正项,提高系统鲁棒性。
将(38)代入(37)有
(39)
又因为
(40)
则
(41)
进一步整理,可得
(42)
其中,
(43)
故根据李雅普诺夫函数第二法,系统(4)是稳定的。根据上述分析,可得如下定理结果:
定理1:基于假设1至假设3,虚拟控制器(11)、(19)和(27),控制器(36)和自适应律(38),考虑一个具有输入饱和的全状态约束的非线性严格反馈系统(4),如果满足初始状态
,则有以下性质成立
1) 误差变量是有界的;
2) 不违反全部状态约束;
3) 闭环系统的全部信号是有界的。
证明:
根据公式(33)和公式(42),A和B按(43)取值,再将公式(42)乘
,对乘积之后的结果在
上取积分得
(44)
结合公式(31)和公式(45)有
(45)
(46)
再根据(47)和(48)有
 (47)
(47)
(48)
根据(49)和(50)得到误差变量
,
满足
(49)
(50)
由此可见
,
是一致最终有界的,又因为误差变量
且
是有界的,所以
也是有界的。所以再根据公式(13)可知作为的关于
,
,
和
的函数,
也是有界的。
根据(47)和(48)还可以得到
(51)
 (52)
(52)
则可得
(53)
根据(53)可知
是有界的,又因为
,且
是有界的,所以
是有界的。剩下的信号的有界性可以通过归纳证明。假设
是有界的,然后有
也应该是有界的。剩余信号的有界性可以通过归纳证明。根据
,
的有界性可以推出。根据光滑性
,
和
也有界。因为
是
,
,
,
的函数,因此它也是有界的。通过归纳,可以得出状态向量
和实际控制输入v,其中v是关于
,
,
和
函数,因此v也是有界的。因此,将所采用的神经网络构造在足够大的逼近区域上,可以得到一个稳定的自适应神经控制器,使有界初始条件保证闭环系统中所有信号的有界性。根据(42)和引理1,很容易证明,闭环系统的所有信号最终都是一致有界的。
3. 仿真实验
为检验方案可行性,根据所设计的控制方法对如下具有全状态约束的非线性严格反馈系统
(54)
其中,
和
是状态变量,状态的约束描述为
,
; u是系统的输入,y是系统的输出,针对系统(1)设计自适应神经网络控制器使得输出y尽可能地跟踪上期望的轨迹
,同时闭环系统的所有信号都是一致最终有界的(图1和图2)。

Figure 1. The trajectories of the state x1 and the reference signal yd
图1. 状态x1及参考信号的轨迹
控制器的设计如下
其中,误差变量
,
,
,
。

Figure 2. The trajectory of the state x2
图2. 状态x2的轨迹
设计自适应律如下
状态初始值设置为
,
,自适应律初始值设置
,
。参数设计为
,
,
,
,
,
,给定常数
,
,
,
。
根据以上的设计方法,用MATLAB仿真进行仿真,所得的仿真曲线描述于图1~6。图1是y跟踪
的轨迹和状态
的轨迹,图2是状态 的轨迹,从图1和图2可以看出所设计系统很好地跟踪,并且状态变量都是有界的;图3是误差变量
、
的相位轨迹图,很清晰的表达出误差在很小的范围内波动;图4是自适应律
和
的轨迹,易知,自适应律有界;图5和图6分别是控制器u和饱和器输入v的轨迹,从而可以看出u和v都是有界的。图1说明跟踪效果良好,且约束条件不违反;图2说明系统状态有界,且不违反约束条件;图3说明误差均在很小的范围内波动;图4~6说明自适应律、控制器及饱和执行器输入均有界。因此,综合图1~6,该方案的优势和准确性得到了较为良好的验证。
的轨迹,从图1和图2可以看出所设计系统很好地跟踪,并且状态变量都是有界的;图3是误差变量
、
的相位轨迹图,很清晰的表达出误差在很小的范围内波动;图4是自适应律
和
的轨迹,易知,自适应律有界;图5和图6分别是控制器u和饱和器输入v的轨迹,从而可以看出u和v都是有界的。图1说明跟踪效果良好,且约束条件不违反;图2说明系统状态有界,且不违反约束条件;图3说明误差均在很小的范围内波动;图4~6说明自适应律、控制器及饱和执行器输入均有界。因此,综合图1~6,该方案的优势和准确性得到了较为良好的验证。

Figure 3. The phase trajectories of the errors z1 and z2
图3. 误差变量z1和z2的相位轨迹
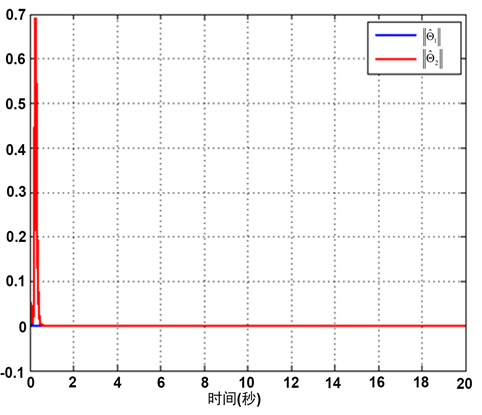
Figure 4. The curves of the adaptive laws
and
图4. 自适应律
和
的轨迹
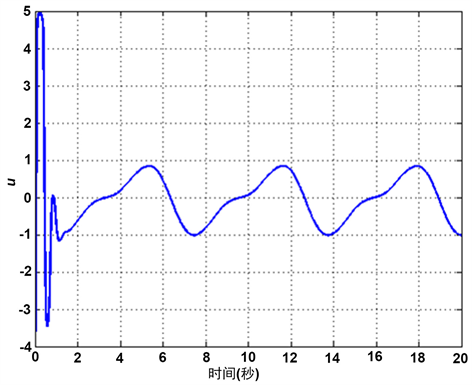
Figure 5. The curve of the system input u
图5. 系统输入u的轨迹
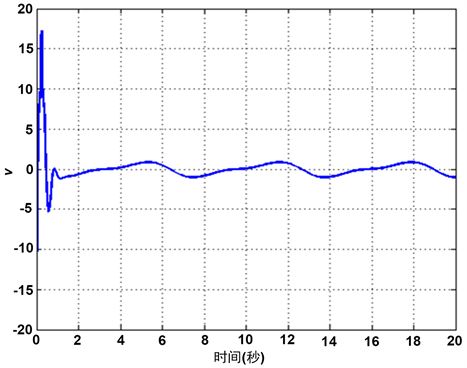
Figure 6. The trajectory of the saturated input v
图6. 饱和输入v的轨迹
4. 结论
本文研究了不确定非线性单变量严格反馈系统的智能约束控制问题。被考虑的三角结构系统,包含了执行器的饱和输入模块。利用径向基神经网络对系统中的未知动态进行辨识,采用高斯误差函数建立出非对称饱和执行器的模型,构造正切型的障碍李雅普诺夫函数来解决系统所有状态必须满足约束条件的问题。基于李雅普诺夫稳定性原理和反步递推技术,证明了闭环系统所有信号的有界性,确保了跟踪误差保持在原点的小邻域内,保证了状态约束条件不被违反。最后,利用数值仿真验证了所提神经网络控制方法的有效性和可行性。
基金项目
辽宁省高校基本科研业务费重点项目(JZL201715402),辽宁省高等学校创新团队(LT2016006)。