1. 引言
随着城市化的发展,城市中的高层超高层建筑不断增多,基坑也往更深更大的方向发展。支护结构对基坑整体的安全性至关重要,支护结构的失效往往会造成严重的安全事故,例如,支护结构强度不足引起的破坏会导致边坡的塌陷,过大的支护变形易造成周边地表的下沉,从而造成严重的生命财产损失。现阶段,城市中的深大基坑越来越多,支护结构的安全更加重要,因此,对基坑支护结构的变形进行精准的预测具有深远的意义。
目前,国内外已经有许多学者在相关领域进行了研究。基坑支护变形的预测方法大致可分为传统方法和新型智能方法。传统方法包括曲线拟合最小二乘法、双曲线模型、幂多项式模型、灰色模型等等,新型智能方法包括神经网络方法、灰色模型方法以及支持向量机等。传统方法方面,王小生等 [1] 采用最小二乘法对基坑开挖引起的建筑沉降监测数据进行了分析,用三次曲线拟合了其演化规律,赵慧军 [2] 采用数学函数拟合了基坑开挖支护结构的变形规律并提出了相应的控制方法,徐日庆等 [3] 基于影像源法预测了基坑开挖引起的土体水平位移,考虑了土体非均匀性的影响,刘美麟等 [4] 提出了改进MSD法并基于此分析了内支撑结合柔性围护结构支护的深大基坑开挖及支护过程的影响,对支护结构的变形展开了动态预测。随着智能算法和计算机性能的发展,近年来,新型智能方法在基坑预测领域的应用也越来越多。灰色模型方面,孟雪 [5] 等基于层次分析法选取了基坑关键要素,结合灰色GM (1,1)和神经网络建立了基坑周边地表的沉降预测模型。支持向量机方面,刘斌 [6] 基于粒子群算法和混沌理论,构建了混沌优化PSO-SVM模型对基坑变形进行了预测。神经网络方面,王成汤等 [7] 针对地铁车站基坑施工,提出了基于多态模糊贝叶斯网络的深基坑坍塌风险预测方法,郭健等 [8] 构建了小波网络W-RBF预测模型,并对经过小波虑噪后的基坑沉降数据进行了预测,宋楚平 [9] 采用基于遗传算法的BP神经网络模型对基坑的沉降进行了预测,张宏等 [10] 建立了深基坑非施工期钢支撑轴力BP神经预测模型,使用Matlab软件进行了模型训练,并用实测数据进行了验证,韦猛等 [11] 基于T-S模糊神经网络构建了多信息融合模型,实现了对深基坑安全预警信息进行智能分析处理。
本文基于BP神经网络模型,针对湖南某变电站基坑支护结构变形监测数据进行分析,以墙顶水平位移和墙顶竖向沉降作为预测对象,选取典型测点并将其80天的监测数据作为样本,进行模型训练和预测,在此基础上,选取部分测点对其模型扩大训练集进行预测结果优化。
2. BP (Back Propagation)神经网络
BP神经网络的学习过程由信号的正向传播与误差的反向传播两个过程组成 [12]。正向传播时,输入样本从输入层传入,在隐层进行逐层计算,然后将结果输出到输出层 [13]。计算输出层的输出与实际输出的差值,开始反向传播阶段:将输出误差以某种形式通过隐层向输入层逐层反传,并基于误差修正其中的相关参数,从而实现网络的训练,此误差信号即作为修正各单元权值的依据。BP网络由输入层﹑输出层和隐层组成,如图1所示,在该BP神经网络中,有p个输入,o个输出,还有q个隐含单元,以此实现从p到o的映射。
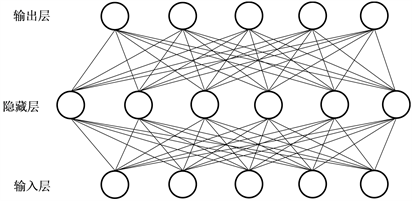
Figure 1. Principle of BP neural network
图1. BP神经网络原理示意图
对于BP神经网络的输出层和隐藏层,正向计算时,每个神经元的输出计算公式可表示为:
(1)
其中,
为该单元的输入,wi为前一层第i个单元的权值,xi为前一层第i个单元的输出值,n为前
一层单元总数,f为激发函数,输出为1或0,θ为内部阈值。
反向传播算法(Backpropagation Algorithm,简称BP算法)是一种常用的训练算法,可用来学习多层结构网络的权值,目标是最小化网络输出值和实际值之间的误差平方,采用梯度下降法对权值进行更新,每次训练的权值调整由三个方面因素决定,分别为学习率,本层误差值,本层输入值。神经网络的训练过程,即是对权值的计算和调整。
BP算法是基于对误差的修正进行训练的,学习率是BP算法的重要部分,学习率的大小对收敛速度和训练结果有很大影响:学习率过小会导致收敛速度慢,而学习率过大又易出现权值振荡的情况 [14]。因此常需要对BP神经网络网络进行一定的改进,目前常用的方法有可变学习率法,遗传算法 [15] 、共轭梯度法 [16] 等。本文采用变化学习率的方式对网络进行优化,预先设定一个迭代次数阈值,当迭代次数超过该值时,对学习率进行一定程度的折减,以变化的学习率实现网络的优化。
3. 基于BP神经网络的基坑支护结构变形预测
3.1. 数据选取与处理
本文基于湖南某变电站基坑的支护结构变形数据,根据其支护结构变形的情况选取关键节点进行预测。所选基坑的支护结构为地下连续墙,主要的监测项目为墙顶水平位移与墙体沉降,考虑该基坑东面紧邻高层建筑,将东侧的地下连续墙变形作为主要的预测对象,以对潜在的变形趋势进行预测。
根据东侧地下连续墙的变形情况和测点布置,选取墙顶水平位移测点D3与墙顶竖向沉降测点Q5作为预测对象,将其连续80天的监测数据作为数据集。对数据集进行划分,前80%的数据作为训练集,后20%的数据作为测试集,训练集中,选取10%的数据作为验证集。为了避免数据的绝对值对网络的性能产生影响,需要对选取的训练集进行归一化处理:
(2)
其中,xi为第i个样本的值,μ为数据集均值,σ为数据集的标准差。
3.2. 墙顶水平位移预测
选取代表性测点D3与D22作为样本,整理其监测数据,建立BP神经网络,网络包含输入层、隐藏层、输出层,其中输入层与输出层神经元个数为1,隐藏层为单层,神经元个数为50,采用降低学习率的方法对模型进行优化,初始学习率为0.01,在125次训练次数后学习率折减为0.005。基于该BP神经网络模型,输入训练集进行学习,当训练集误差逐渐减小而验证集误差逐渐增加时,可认为BP神经网络模型进入了过拟合阶段,此时停止训练,完成BP神经网络的训练。
所用模型的隐藏层结构和神经元个数通过随机搜索法 [17] 得到,训练过程如图2所示,最佳训练次数为250次左右。
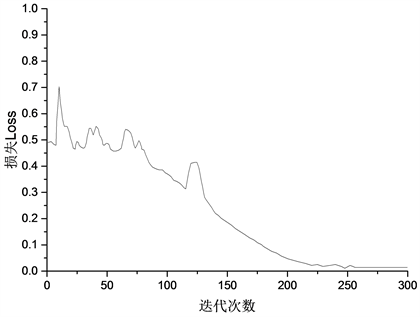
Figure 2. Training process of BP network predicting horizontal displacement
图2. 墙顶水平位移预测BP神经网络模型训练过程
基于训练后的BP神经网络模型对D3和D22第66至81天的水平位移进行预测,预测结果和实际监测值的对比如图3与图4所示。整体上BP神经网络对于位移变化趋势预测较为准确,能较好地反应测点水平位移的整体发展趋势,但同时存在误差较大的预测点。图3中对D3测点的预测,较好地预测出了该测点位移先增加、后减小、再增加的变化趋势,但是预测的位移值均偏小于实际观测值,同时,在个别时间段的预测结果偏差较大,主要表现在第73至78天预测值与观测值的误差均突破了0.5 mm。图4中对D22测点的预测结果,反应了其先小幅波动再大幅增长的趋势,尤其对于第70至74天的起伏,以及第80天后的水平位移大幅增长都进行了准确的预测,但在个别节点,如第67天,第71、72天,第77、78天误差相对较高。整体而言,该模型对支护结构水平位移的整体变化趋势预测较准确,其对支护结构水平位移随着时间的增减预测具有较高的参考性,但模型对具体时间节点的水平位移预测结构精确度相对较低。
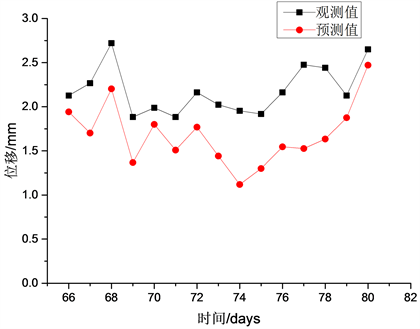
Figure 3. Prediction of the horizontal displacement of D3
图3. 测点D3墙顶水平位移预测结果
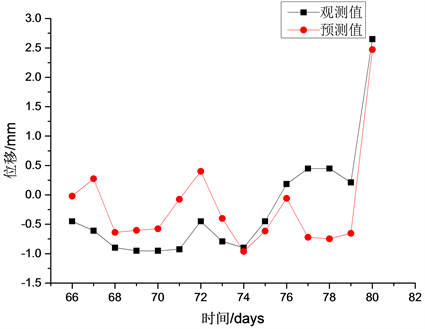
Figure 4. Prediction of the horizontal displacement of D22
图4. 测点D22墙顶水平位移预测结果
3.3. 墙顶竖向沉降预测
基于同样的原理,选取代表性测点Q5与Q12,对其墙顶竖向沉降进行预测。建立BP神经网络,采用随机搜索法,确定最佳网络结构:输入层与输出层神经元个数为1,隐藏层为单层,隐藏层神经元个数为50。采用降低学习率法对训练过程进行优化,初始学习率为0.01,迭代100次后下降为0.005。将训练集输入模型进行训练,训练过程如图5所示,最佳训练次数为200。基于训练后的BP神经网络模型对测点Q5与Q12墙顶竖向沉降进行预测。
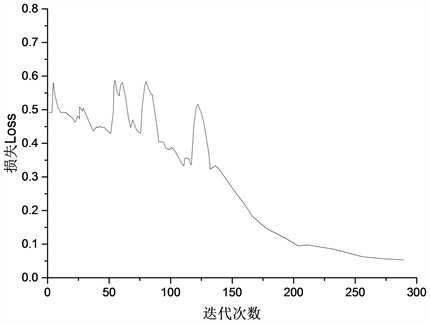
Figure 5. Training process of BP network predicting vertical settlement
图5. 墙顶竖向沉降预测BP神经网络模型训练过程
对测点Q5的第66至82天的墙顶竖向沉降预测结果与实际监测值的对比如图6所示,预测得到的竖向沉降曲线趋势与实际观测的沉降曲线发展趋势基本吻合,说明该预测能较好地反应竖向沉降变化的趋势,具体而言,预测曲线对72至76天的沉降波动做出了较好地预测,并成功预测了该周期初期和末期的沉降平稳发展趋势,然而,该模型预测的沉降均值大于实际监测值,并在个别时间点的预测值出现了较大的误差,如第70天、72天、73天、74天。测点Q12墙顶竖向沉降预测结果如图7所示,其较好地反应了沉降先增大后减小的整体趋势,并预测了沉降趋势的小幅波动,但其同样在个别节点出现了相对大的误差,如第75、79、80天。预测结果说明该模型在沉降发展趋势方面预测准确,而对具体沉降值的预测精确度有待提高。

Figure 6. Prediction of the vertical settlement of Q5
图6. 测点Q5墙顶竖向沉降预测结果
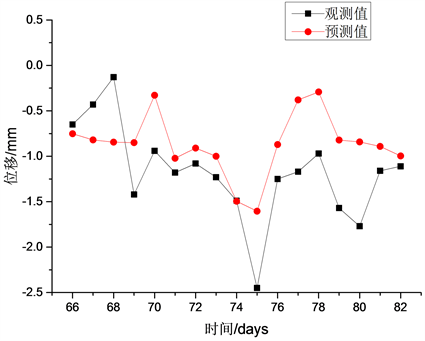
Figure 7. Prediction of the vertical settlement of Q12
图7. 测点Q12墙顶竖向沉降预测结果
3.4. 扩大训练集后的预测结果
对于BP神经网络而言,预测的准确度与训练集的大小有密切的关系。基坑支护结构的变形问题是一个复杂的多特征变化问题,要得到更加可靠的预测模型,就需要更多准确的训练数据。因此,针对3.2,3.3中所得到的预测结果,对墙顶水平位移D3测点和墙顶竖向沉降Q12测点的预测训练集,额外加入前序50天的监测数据,以增大训练集的大小。扩大训练集后的预测结果如图8和图9所示。
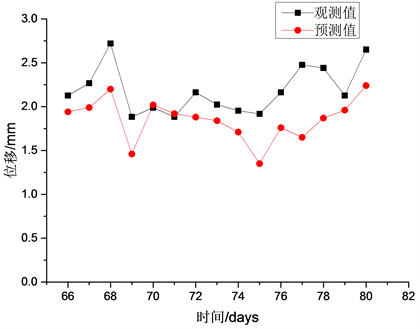
Figure 8. Prediction of the horizontal displacement of D3 after expanding training set
图8. 扩大训练集后的测点D3墙顶水平位移预测结果
对比图3与图8,可以发现扩大训练集后的测点D3墙顶水平位移预测结果精确度有所提高,在扩大训练集之前预测结果平均误差0.51 mm,扩大训练集后的预测结果平均误差降低为0.36 mm,误差的减小说明训练集增大有助于整体预测精确度的提高。同时预测得到的墙顶水平位移变化趋势也与真实情况更加贴合,基本反映出了其波动的规律。
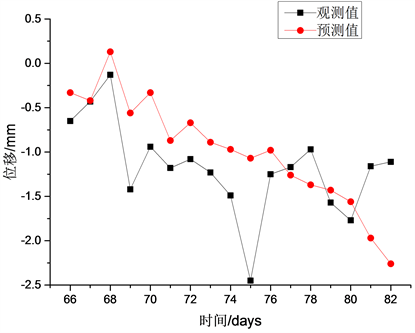
Figure 9. Prediction of the vertical settlement of Q12 after expanding training set
图9. 扩大训练集后的测点Q12墙顶竖向沉降预测结果
对比图6和图9,发现扩大训练集后Q12墙顶竖向沉降预测结果整体精确度没有明显提高,预测结果平均误差由0.47 mm升高为0.48 mm。观察扩大训练集后预测得到的墙顶竖向沉降变化趋势,发现扩大训练集后的预测结果在预测区间的前8天预测的趋势更加准确,但是在后8天的预测结果偏差变大了。分析其原因,新增的监测数据加强了对一部分沉降变化规律的学习,因此预测区间前半段的预测结果有显著改善,但是其监测数据中可能存在异常数据,对其他部分沉降变化规律的学习造成了干扰,导致预测结果后半段偏差有所扩大。
3.5. 预测结果分析
本文采用BP神经网络对基坑支护的墙顶水平位移和竖向沉降进行了预测,预测结果表明,在本例中,BP神经网络对墙顶水平位移和竖向沉降的整体发展趋势和局部波动可以实现准确的预测,但是对具体时间点的位移或者沉降预测值的预测精确度有待提高。在此基础上,本文扩大训练集重新训练了BP神经网络,对墙顶水平位移测点D3和墙顶竖向沉降测点Q12新增了前序50天监测数据至模型训练集中,结果表明预测精度整体有所上升。
预测结果与真实值存在较大的局部误差,分析原因,第一是因为本模型在实现预测一段时间的位移和沉降时,其后续天数的预测值是由前面预测值输入预测模型得到的,因此前面预测值的误差会影响后续天数预测的结果,导致误差积累,越往后时间的预测结果越不准确;第二,BP神经网络的训练需要基于大量的训练样本,训练样本越充分准确,得到的预测模型越可靠,对于本基坑支护结构而言,其监测数据相对较少,训练样本不足;第三,现场监测手段数据存在一定的错误和异常,异常值对模型的训练存在显著的影响,最终导致预测精度的下降。
4. 结论与展望
本文基于BP神经网络模型对湖南某变电站基坑地下连续墙的墙顶水平位移和竖向沉降进行了预测,取得了较准确的预测结果,并在此基础上扩大模型训练集后进行了预测,提高了预测精准度,并对其中产生的误差进行了分析,得到的主要结论如下:
1) 本文通过BP神经网络模型实现了较准确的支护变形预测,说明神经网络模型对基坑支护结构的预测具有较高适用性,基坑支护结构变形受到许多因素的影响,其作用机理复杂且具有很强的规律性,传统方法难以构建准确的预测模型,而神经网络模型具有强大的拟合能力,可以很好地预测基坑支护变形的发展趋势。
2) 本文通过扩大模型训练集,提高了BP神经网络模型的预测精度,说明BP神经网络模型的精度非常依赖于训练集的质量,在工程应用中,应尽可能地用有效数据扩大模型训练集。
3) 通过可变学习率法有效减小了模型训练的时间,使其可以快速收敛并保证训练效果,说明可变学习率法对神经网络训练过程具有良好的优化效果。
4) 训练集中的异常值对模型的训练具有显著影响,导致BP神经网络预测的准确度下降,说明训练集的准确度和神经网络预测精度直接相关,更多的有效训练数据可以促使模型的预测精度和泛化能力进一步提高,在实际应用中,应注意排除训练集中的异常数据,同时基于数据量大小对网络结构进行相应的调整,以保证模型的精度。
NOTES
*通讯作者。