1. 引言
近些年来,聚类是无监督学习中的热门方法之一。聚类是许多应用过程中的非常重要的一环,包括机器学习,计算机视觉,信号处理,模式识别等。近些年来国内外很多研究学者已经提出了许多的聚类方法,包括基于划分的聚类(K-Means,K-Medoids) [1] [2],基于层次的聚类(CURE) [3],基于模糊理论的聚类(FCM) [4],基于密度的聚类(DBSCAN) [5],基于图的聚类(Spectral Clustering) [6],基于核的方法 [7]。其中,谱聚类和基于密度的聚类是当下比较热门的方法之一,它们通常表现出良好的聚类性能。基于密度的聚类的优点是能够找到任意形状的聚类并且对噪声具有鲁棒性。密度聚类算法假设聚类结构可以通过样本分布的紧密性来确定。通常密度聚类算法从样本密度的角度考虑样本之间的连通性,并基于可连接样本不断扩展聚类以获得最终的聚类结果。基于密度的噪声应用空间聚类(DBSCAN) [5] 是一种众所周知的方法,它基于一组邻域参数(ε和MinPts)来表征样本的数据结构。但是这两个参数ε和MinPts并不直观且难以选择。
谱聚类算法是一种基于图论的聚类算法 [6] [8]。谱聚类基于数据集构造无向图,并使用非负相似矩阵表示整个无向图,从而得到一个相似度矩阵再得到拉普拉斯到矩阵,然后进行特征分解。最后通常使用K均值算法对结果进行后处理以获得聚类指标。谱聚类具有以下优点:(1) 易于实现;(2) 聚类结果更好,约束更少;(3) 分割非线性可分离数据的效果具有明显的优势;(4) 具有以下优点能够在任何形状的样本空间上聚类并收敛到全局最优解。基于其受欢迎程度和上述几个优点,很多研究人员提出了许多谱聚类算法。Donath W E等人 [9] 首先提出了相似矩阵的特征向量。找到相似矩阵的第二个特征向量可以将数据分为两个簇 [10]。Hagen和Kahng在1992年提出的比率削减在最小化类之间的相似性时引入了类尺度的平均项,并建立了基于矩阵谱分析谱聚类算法 [11]。 [12] 提出的归一化割,解决了一类最小割中只有一个或几个孤立点的倾斜分割问题。 [13] 提出了NJW算法(嵌入式特征空间上的K-means算法)。
对于给定的数据集,谱聚类基于成对相似性将数据表征为加权无向图中的节点。谱聚类的目标是将无向加权图分为两个或多个子图,以使子图的内部节点相似而子图之间的节点是不同的。然后,使用非负相似度矩阵表示整个无向图,再进行特征分解,最后通过传统聚类从特征向量中获得最终的聚类分配。总之,相似度矩阵的构建直接影响聚类效果。因此,谱聚类的相似矩阵构造问题是一个关键点 [14]。通常,通过相似矩阵获得拉普拉斯矩阵,然后直接选择对应于前k个特征值,最后一步再进行k-means。根据矩阵扰动理论,矩阵特征值之间的差异称为本征间隙(Eigengap) [15],矩阵扰动理论中的Davis-Kahan定理 [16] 表明,块对角矩阵的特征向量与矩阵对角关系相似度矩阵的子空间也由eigengap确定,eigengap越大,由k个特征向量形成的子空间就越稳定 [15]。 [17] 从图的划分角度出发,提出了一种定义相似度图的新方法。尽管此方法有助于推断数据集的内在结构,但是在无监督条件下获得的相似度矩阵并没有得到根本改善。 [18] 提出了一种局部密度自适应相似度测量方法。该方法可以放大同一类中具有公共交集的样本之间的相似度,但是不会更改没有公共交集的样本之间的相似度。
尽管谱聚类算法在过去的研究中取得了长足的进步,并且与其他聚类方法相比具有许多优点,但是常用的方法也容易出现以下两个缺点:传统聚类算法构造的相似度矩阵不能很好地考虑数据集的分布结构,很难真实地反映出数据点之间的相似度。最常用的相似度函数是高斯核函数,仅考虑数据的第K个最近邻居,不够全面的并且忽略其相邻点的分布。
为了克服上述两个缺点,本文提出了一种新的相似度矩阵构造方法,该方法受到密度聚类的启发,以求出数据之间的k个最近邻关系(KNRS)。在实验中,与广泛使用的k均值聚类、NJW谱聚类(SC)、模糊聚类FCM、SCMSA谱聚类算法作比较,实验结果表明,我们通过新方法构建的相似矩阵不仅eigengap增加了,新的聚类也具有许多基本优点。主要贡献有两个方面:(1) 在我们的新方法中,考虑数据的k邻域分布,该模型可以方便,准确地发现数据集中包含的密度信息。可以反映数据的内在结构。(2) 关于聚类结果,eigengap变得更大,因此矩阵分区稳定。
本文的其余部分安排如下。在第二节中,我们介绍了有关谱聚类的相关工作。在第3节中,我们提出了基于相似度矩阵聚类算法的新方法。在第4节中,对各类数据集的实验结果进行了分析。在第5节中总结本文。
2. 谱聚类算法及分析
2.1. 谱聚类
谱聚类是一种基于图论的聚类方法,目的是将聚类转化为图分割。基于图论的最佳划分标准:最大化位于同一子图中的样本点之间的相似度,并且最小化位于不同子图中的样本点之间的相似度。谱聚类可以大致分为以下步骤:第一步:预处理构造表示数据集的图形和相似矩阵。(计算度矩阵D,度矩阵是对角矩阵,其元素是点的度数。)第二步:谱表达,根据相似矩阵,得到相应的正则化或不规则拉普拉斯矩阵,计算L的第一个特征向量。通过拉普拉斯矩阵的特征分解,得到特征值及其对应的特征向量。第三步:选择特征向量以形成特征空间,并通过聚类算法(例如K-means算法)将特征空间离散化(可以在最后阶段使用除k-means之外的简单算法,例如simple linkage,k-lines,elongated k-means,混合模型等)最后获得聚类结果。
从图的划分角度来看,谱聚类根据所使用的划分标准将算法分为两类,即2-way谱聚类和k-way谱聚类。2-way谱聚类:Perona和Freeman提出的PF [19],它是最简单的迭代2路分区算法,提出与相似矩阵W的第一特征向量聚类。Shiand Malik在2000年提出了SM方法 [12] SM算法对获得的拉普拉斯矩阵进行特征分解,并采用第二个小的特征向量(即Fiedler向量)进行聚类。在Fiedler向量中大于某个值的数据点属于一个类别,小于某个值的数据点属于另一个类别。Scott等人提出了SLH重定位方法 [20]。 Ding等人提出了Mcut方法 [21],Mcut算法可以产生更加均衡的分区结果,尤其是当类之间的重叠很大时,效果更加明显。近年来,已经发现使用更多特征向量并直接计算k-way分割会得到更好的聚类结果 [22] [23]。NJW算法通常被称为最经典的多向谱聚类算法,由Ng等人 [13] 提出,该算法直接选择与Laplacian矩阵的前k个特征值相对应的特征向量进行正则化。MS方法是由Meila等人 [24] 提出的,Meila将相似性解释为马尔可夫链中的随机游动,并分析了该随机游动的概率传递矩阵。
2.2. 相似度矩阵
给定数据集
,
其中d是每个点的维数。我们首先将这些数据点映射到无向图
,可以得到一个
矩阵W表示整个无向图,其元素Wij表示边缘权重且
,表示两个顶点之间的相似性。构造相似矩阵的大多数方法都是数据集的稀疏表示,并且具有计算优势。以下是一些构建方法:ε-邻图,k最近邻图和完全连通图。一般通常使用全连接图的方法但这种构造仅在相似度函数对局部邻域建模时才有用。选择相似度函数会极大影响之后谱聚类的结果。点的特征在于它们的成对相似性,即与每对点
相关联的是相似度值
。相似性矩阵
由项wij组成,这些项可以是:余弦型,模糊型,高斯类型。在大多数情况下选择高斯核函数,而其他相似性(例如余弦相似性)用于特定应用。最初提出相似矩阵的特征向量用于划分数据是由Donath等人提出 [9]。Fiedler发现相似矩阵的第二特征向量可以将数据分为两个簇 [10],Hagen和Kahng在1992年提出的“比率削减”在最小化类之间的相似性时引入了类尺度平均项,并建立了基于矩阵谱分析 [11],之后,学者们也提出了许多构建相似度矩阵的方法。R. Liu等。提出的FLR-MRW方法假定正则矩阵通过对正则矩阵的核规范项进行正则化来假设其亲和度较低 [25]。BD-LRR关注子空间聚类的相似度矩阵的构建 [14]。提出了局部密度自适应相似度测量的频谱聚类SC-DA方法 [18]。 [26] 提出了一种基于邻域传播在谱聚类中构造亲和度矩阵的方法。 [27] 提出了一种基于模糊的学习算法,用于AFSSC谱聚类。
2.3. 本征间隙
理想情况下,能否在相似度矩阵中反映相互分离的k个数据集的间隔,应该使该阵对角线上分布k个全1分块矩阵,其余位置都为0。实际上,构造这样的亲和力矩阵是困难的。通过矩阵扰动理论已知,实际相似度矩阵对角线上的块矩阵元素不全为1,块对角矩阵外的元素也不全为0。而分别是全1矩阵加上一个负的扰动量和一个正扰动量。根据矩阵摄动理论,由相似度矩阵得到的拉普拉斯矩阵的第k个和第k + 1个特征值之间的差称之为本征间隙(Eigengap),本征间隙越大,选取的k个特征向量所构成的子空间就越稳定 [15]。
在线性代数中,线性算子的特征是两个连续特征值之间的差异,其中特征值以升序排序。在谱聚类中,eigengap通常称为谱间隙:(以钱德勒·戴维斯(Chandler Davis)和威廉·卡汉(William Kahan)的名字命名的戴维斯·卡汉定理,用eigengap表示算子的本征空间在扰动下如何变化。块对角相似度矩阵矩阵和实感矩阵也由eigengap确定,eigengap越大,由k个特征向量稳定形成的子空间就越多 [15] [28]。 [29] 基于eigengap和正交特征向量提出了自适应谱聚类。
3. KN-SC算法及证明
为了清楚地描述我们提出的新方法。我们首先在第3.1节中定义基本概念,然后在第3.2节中描述建议的KNRS方法。
3.1. 概念定义
给定数据集,
,d是每个点的维数。
定义1:k近邻图矩阵A。
点之间的欧几里得距离定义为:
(1)
(2)
k是KNRS的参数,k用于找出每个点的k个最近邻。
定义2:k近邻关系
。
(3)
式(3)是归一化的。是KNRS的参数通常用于调整,可选参数的范围易于确定,用户可以轻松快捷地选择最佳参数。(根据重复的实验验证和结果比较,值通常为0.8,0.9)。x是矩阵A的每一行的总和除以k。
(4)
定义3:eigengap δ。
定理1:根据Davis-Kahan定理,
为对称矩阵,而
为frobenius范数或矩阵的2范数。将
视作A加扰动。令
为间隔。用
表示包含在其中的A个特征值的集合,用V1表示与所有这些特征值相对应的本征空间,将
之外的A的谱与
之间的距离定义为:
(5)
和
之间的距离
的范围为:
(6)
这表明,d越小越好,越接近理想分割,δ越大d值便越小即效果越好。在本文中我们将δ定义为eigengap。
3.2. KNRS算法
KNRS方法包括五个阶段,大致流程如图1所示。
第一步:为所有的数据点构造完整的连接图(每个样本的邻居数),我们使用到完整连接图的欧几里德距离并获得连接矩阵。按距离d排序,根据给定k的数量选择最近的k个点。根据等式(2),最后我们得到一个最近邻图矩阵A。
第二步:找到k个邻居关系
。根据等式(3),我们得到k个邻居关系
。由于相似矩阵具有对称性,因此将
转换为对称矩阵可得到最终
。通过
的模型可以方便准确地发现数据集中包含的密度信息。可以反映数据的内在结构,考虑到邻居对他们密度的影响。生成的新亲和度矩阵可以增加应该在同一类中的点对的相似度,并使近点越来越近。使改进的算法对离群点不那么敏感。
第三步:得到KNRS相似度矩阵W。基于完全连接图和k邻居关系
计算的相似度矩阵,更新相似度矩阵。(此类相似性函数的一个示例是高斯相似度函数,其中参数控制邻域的宽度)。
根据上述步骤获得的更新的相似度矩阵,KNRS相似度矩阵W不仅考虑了其邻居的分布,而且还充分考虑了数据集的分布结构,真正体现了数据点之间的相似度。
第四步,根据相似度矩阵,得到相应的正则化或不规则化的拉普拉斯矩阵,通过对拉普拉斯矩阵进行特征分解,得到特征值及其对应的特征向量。计算D矩阵,度矩阵D是对角矩阵,其元素
是点
的度。拉普拉斯矩阵 [30] [31] [32] 通常分为两类 [6]。非正则化拉普拉斯矩阵和正则化的拉普拉斯矩阵。
非正则化拉普拉斯矩阵定义为:
(7)
正则化拉普拉斯矩阵分为两种矩阵(
和
):对称正则化的拉普拉斯矩阵和非对称正则化的拉普拉斯矩阵。
定理2:G是具有非负权重的无向图,具有k个连通子图
。
和
的特征值0的数量等于图中连接子图的数量。对于
来说,特征向量
划分k个特征空间,对于
来说,可通
过特征向量
获得k个特征子空间。两个矩阵彼此密切相关,并定义为:
(8)
. (9)
命题1:方程(8)正则化拉普拉斯矩阵的性质。
对于每一个
,我们都有等式(10)。
和
是正半定值,并且具有非负实值特征值
,最小特征值是0。
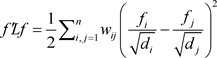 (10)
(10)
由于上述定理2和命题1:
证明1:证明方程式
(11)
最后,得到拉普拉斯矩阵L,然后选择特征向量形成特征向量空间,并在特征向量空间中采用聚类算法如k均值算法。算法流总结为:
1. 第一步,构建完整的连接图并选择最近的k个点,获得k个最近的邻居矩阵W。
2. 第二步,找到k邻居关系。
3. 第三步,获得新的相似矩阵W。
4. 第四步,获得拉普拉斯矩阵L。
5. 第五步,使用例如K-均值算法得到最终的聚类结果。
3.3. KNRS算法相关证明
由于(等式(8)),得到
,eigengap取决于L的特征值,L的特征值基本上由
确
定。令
为计算特征值的函数。
引理1:
下限的渐近分析:
(12)
矩阵A的每个特征值的模数(绝对值)不超过矩阵A的范数
。
。“~”代表渐近分析。
(13)
(14)
引理2:
上限的渐近分析:
(15)
设sup (L)的上限和sub (L)下限,则差为∆ (
)。根据引理1和引理2:
(16)
引理3:eigengap的边界取决于
。根据戴维斯–卡汉(Davis-Kahan)定理1和方程式(7),(这里我们将KNRS度矩阵和KNRS相似度矩阵分别称为D'、W'),然后,我们对原始L和A进行运算,效果取决于H'和eigengap。
定理3:由矩阵的谱半径(即矩阵的特征值)不超过矩阵的任何范数可得:
(17)
与以前
相比,eigengap变大。
4. 实验
在本节中,我们显示了所提出的模型KRNA与一些模型(例如K均值,广泛使用的NJW谱聚类(SC)、模糊聚类FCM,SCMSA算法的结果。显示并列出了实验结果。表1有6个数据集,其中4个来自UCI [33],两个来自人工数据集和Mnist数据集。
4.1. 数据集
Iris数据集包含3个类别,每个类别有50个实例,具有4个属性,其中每个类别都表示一种Iris植物。Wine数据集包含三种葡萄酒中178种样品中每种的13种成分的数量。Soybean数据集有47个样本,35个属性和7个类别。Seeds数据集具有210个样本,7个属性和3个类别。Two circles的人工数据集在两个圆圈中具有420个样本,在两个类别中具有三个属性。Boat数据集包含100个样本,2个属性和3个类别。这两个人工数据集包含两种类型的样本,即中等密度密集区域和周围稀疏区域。MNIST手写数字数据库的训练集为60,000个示例,测试集为10,000个示例,784个属性和10个类别用来验证算法不仅对密度均匀的数据集聚类有效,而且对于密度分布不均匀的数据集聚类也有效。标准数据集用于进一步检查算法的有效性和泛化能力。
4.2. 聚类评价指标
4.2.1. NMI
本文使用称为标准化互信息(NMI)的外部索引。NMI是使用最广泛的外部有效性指标之一 [34] [35]。它用于度量通过聚类方法获得的聚类标签与基础类标签之间的相似度。两个随机向量X和Y之间的互信息为:
(18)
其中
是X和Y之间的互信息,
和
分别是X和Y的熵。具体可以表示为:
(19)
其中
表示Ck类中的元素数,
表示属于第m类的元素数,
表示C类与第m类之间的相交数。上述公式计算的结果越大,聚类效果越好。
4.3. 实验总结分析
4.3.1. 章节标题
在实验中,我们将模型与其他模型的性能进行了比较。表2显示了实验的各个聚类方法NMI在6个数据集(Iris,Wine,Soybean,Seeds,Two circles,Boat)上的结果。关于NMI评估指数,在大多数数据集上,我们的KNRS优于k-means,FCM,SC和SC-MSA。例如,在Wine数据集中,实验结果表明,我们的KNRS模型在基准数据集上实现了最先进的性能。尽管密度稀疏空间和稠密空间如Boat数据集,对谱聚类方法提出了一些挑战,但KNRS方法的性能还是分离的很准确。仅在“种子”数据集中,比SCMSA稍差一点。表2是对6个标准数据集的聚类结果。图2是由KNRS和实际获得的结果,和与SC聚类比较的真是结果。例如在Iris和Two circles数据集上,左边是KNRS的结果,右边是真实的标记效果。

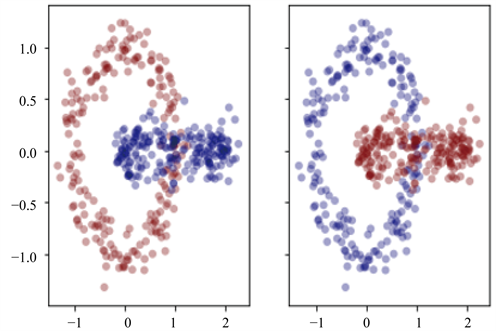
Figure 2. KNRS clustering results on benchmark datasets
图2. KNRS聚类在实验数据上的结果

Table 2. Results on datasets by NMI
表2. 实验数据集NMI结果
MNIST是手写数字数据库如图3所示,对于那些想在真实数据上尝试学习和模式识别方法同时又在预处理和格式化上花费最少精力的人们来说,是一个很好的数据库。本文从MNIST的训练集中选择了500个图像中的150个属性进行实验。NMI对MNIST数据集的聚类结果总结在图4中。根据图4,我们可以看到KNRS方法优于其他比较方法。
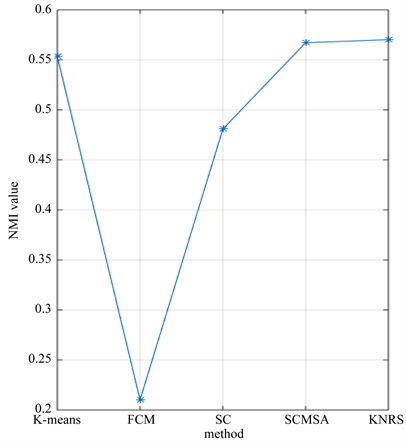
Figure 4. Results on MNIST datasets by NMI
图4. 在数据集MNIST上的NMI结果
关于eigengap值的实验结果显示在图5中。SC-eigengap表示通过SC方法获得的eigengap值,KNRS-eigengap表示通过KNRS方法获得的eigengap值,large-eigengap表示增大的eigengap的值,由实验可知与SC方法相比,KNRS方法增加了eigengap。从图2和图5可以看出,KNRS的性能优于SC,KNRS可以使eigengap更大。图6展示出了使用SC和KNRS方法获得的eigengap值和NMI。在图中,我们可以清楚地看到eigengap和NMI的值增加,这意味着随着eigengap的增大,聚类效果确实会越来越好。
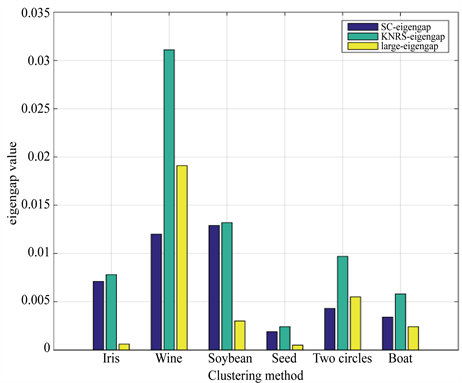
Figure 5. Results of increased eigengap of dataset in KNRS and SC methods
图5. KNRS和SC方法中6组数据集中本征间隙增大值结果
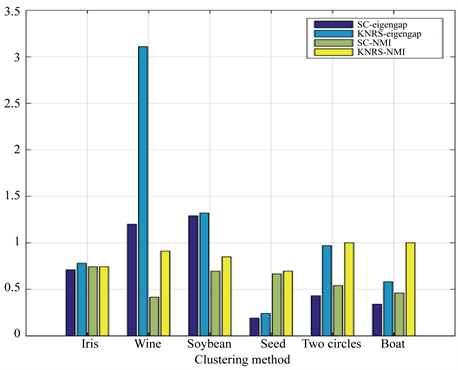
Figure 6. Comparison of the effect of increasing the eigenspace on NMI on 6 sets of datasets
图6. 6组数据集上增大本征间隙对NMI影响的比较
谱聚类的一个关键步骤是为参数选择合适的值。为了观察参数选择对聚类结果的影响,我们在人工数据集Boat上测试了KNRS的性能。图7描绘了参数
从(0.1,0.2,0.4,0.8,1)和参数k从(1,3,5,7,9,10,13,15,16,17,18,19,20,21)以及在Boat上的聚类结果的相应精度值。如图7所示,随着k的增长,聚类效应变得更好,并且在达到最佳效应后趋于稳定。这表明我们的算法对参数是稳定的。结果如图7所示。从这个图可以看出,KNRS对参数不敏感。
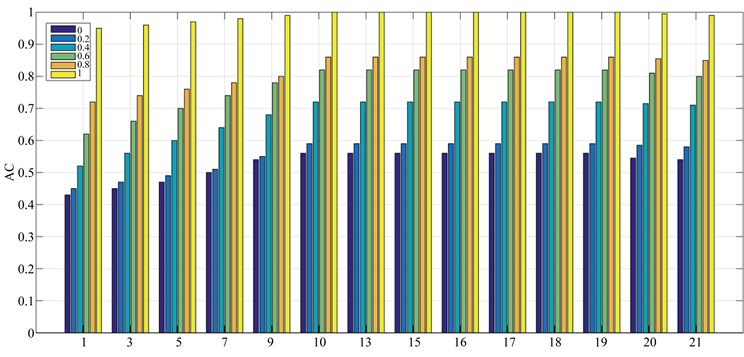
Figure 7. Clustering results of KNRS method for different δ and k. (δ = 0.1, 0.2, 0.4, 0.8, 1); number of neighbors k = 1, 3, 5, 7, 9, 10, 13, 15, 16, 17, 18, 19, 20, 21
图7. 在不同的δ = 0.1, 0.2, 0.4, 0.8, 1与k = 1, 3, 5, 7, 9, 10, 13, 15, 16, 17, 18, 19, 20, 21值下KNRS聚类结果
5. 总结
在本文中,我们提出了一种新的基于k邻域关系构建相似矩阵方法而非传统的用k近邻图或者全连接图构建,经证明确实可以得到具有较大eigengap的拉普拉斯矩阵,从而提升谱聚类效果。我们的新方法中,考虑数据的k邻域分布,该模型可以方便,准确地发现数据集中包含的密度信息。可以反映数据的内在结构。关于聚类结果,eigengap变得更大,因此矩阵分区稳定。无论密度稀疏空间还是稠密空间,KNRS都具有良好的性能,KNRS方法的性能优于其他方法,并且可以更准确地聚类,和提高eigengap。由实验可以看出我们提出的KNRS方法,在七个基准数据集上的实验表明该模型表现良好。我们观察到,所提出的方法明显优于其他一些最新方法。将来,我们计划在其他条件下应用KNRS,并持续完善这个模型。
致谢
时光飞逝,一转眼三年就过去了,在这三年里我学到了很多也成长了很多。上学的时候总是想着什么时候可以工作,但是越来越临近毕业季的时候却越发的留恋。回顾读研究生这短短三年时光,感慨颇多,收获颇丰。很感恩和感激每一个帮助过我的人,感谢我的研究生导师王老师,他的和蔼可亲对学术有很高的追求,循循善诱,勤勤恳恳又很理解学生,非常的让人念念不忘。也感谢我的师兄师姐和师弟师妹们,谢谢大家对我的帮助和支持。最后也要感谢我的父母和一直支持的我的亲朋们。我想以后我要用我学到的知识努力的回报社会,做一个有理想有抱负的人,为祖国的繁荣昌盛添砖添瓦。