基于组合赋权的IDP-CRUTIC的齿轮箱故障评价

Application of Combination Weighting Based IDP-CRITIC Model in Gearbox Failure Evaluation

摘要: 针对现有齿轮箱故障评价需要研究设备机理造成的效率底下、功能性不强的问题，本文提出了基于组合赋权的IDP-CRUTIC的齿轮箱故障评价方法。首先对传感器收集到的振动信号数据进行分析，提取相关特征。然后，绘制不同传感器在不同状态下的振动信号时间序列函数，并对这些函数的特征进行了简要分析。其次，对数据提取了平均值，方差这两个用以描述振动数据的总体趋势的特征变量，以及峰度、偏度这两个对判断齿轮箱齿轮故障有着重要作用的特征变量，并利用SPSSPRO对每一组数据进行了特征数据计算。最后，通过特征数据计算对这些变量进行了基于组合赋权的IDP-CRUTIC的评价模型进行有效性分析，选取的特征均能有效地描述齿轮箱故障。仿真和实验结果表明，所提出的方法更能描述出齿轮箱的故障评价。

Abstract: To address the existing gearbox failure evaluation needs to study the mechanism of the equipment resulting in low efficiency and low functionality, this paper proposes a combination of empower-ment-based IDP-CRITIC of gearbox fault evaluation method. Firstly, the vibration signal data col-lected by sensors are analyzed to extract relevant features. Then, the vibration signal time series functions of different sensors in different states are plotted, and the features of these functions are briefly analyzed. Next, the average and variance, which are the two characteristic variables used to describe the overall trend of the vibration data, and the kurtosis and skewness, which are the two characteristic variables that play an important role in determining the gear failure of gearboxes, were extracted from the data, and the characteristic data were calculated for each set of data by us-ing SPSSPRO. Finally, through the calculation of characteristic data, the effectiveness of these varia-bles is analyzed based on the combined weighting based IDP-CRITIC evaluation model, and the se-lected features are all effective in describing gearbox faults. The simulation and experimental re-sults show that the proposed method is more descriptive of the gearbox failure evaluation.

1. 引言

齿轮箱是现代工业发电机组必不可少的机械装置，其应用范围广泛，例如在风力发电机组、核电齿轮箱、起重机等。齿轮箱是在风力发电机组中应用很广泛的一个重要的机械部件。其主要功用是将风轮在风力作用下所产生的动力传递给发电机并使其得到相应的转速。它的重要功能是将风轮在风力作用下所产生的动力传递给发电机使其得到相应的转速进行发电 [1] 。它的研究和开发是风电技术的核心。我国在“十三五”期间的陆上风电机组的平均单机容量已达到4 MW及以上。在海上风电方面，2020年，东方风电完成10 MW级风电机组样机安装运行。同年，明阳智能发布11 MW级风电机组设计方案。“十四五”初期，风电机组的设计方案达到了16 MW级(国外最大为维斯塔斯的15 MW机型)。风电齿轮箱是双馈型和半直驱型风电机组中传递兆瓦级功率的关键部件，其成本在整机中的占比超过16%，是降低整机成本的重要环节。据全球风能理事会统计，2018年全球双馈型、半直驱型风电齿轮箱的市场占比分别为96%和4%，预计2021年、2022年、2023年全球风电齿轮箱需求分别为45.0 GW、42.8 GW和41.8 GW [2] 。齿轮箱若发生故障，会造成生产效率的降低；若使用时突发情况，严重者更甚威胁到人身安全或造成财产损失，但由于环境复杂，齿轮箱的检测难度极大，检查标准也极难下定义。如何确定齿轮箱的故障评价在各方面应用都具有重要意义。贾兴等人 [3] 根据齿轮箱在发生齿面磨损、齿面点损、齿面胶合以及断齿的故障下会产生磨损颗粒的特点，提出用磨粒的大小、尺寸、形状、累计速率反映齿轮箱的故障程度。P. Caselitz等 [4] 将基于频谱分析方法应用于海上风电机组的状态监测和故障诊断中，其主要利用嵌入式开发技术，同时搭建了整个测试系统。Michael等 [5] 通过监测齿轮箱的振动信号以及风机主轴转速、位移和转矩，通过分析这些信号对风电机组进行故障诊断。徐展等 [6] 通过频域、小波多分辨率分析和时域等方法展示了风电机组传动链的故障诊断过程，并总结出了故障的监测以及故障的诊断方法。以上都是传统的故障评价方法，功能比较薄弱，所以，本研究提出了一种基于数学建模的故障评价方法。早在之前，基于数学建模的诊断方法主要有模糊原理、小波分析、基于线性/非线性判别函数以及贝叶斯判据等方法。此类方法主要通过研究设备故障机理，由此建立数学模型而进行故障诊断 [7] 。由于齿轮箱结构复杂，频率成分多，齿轮箱简易振动诊断方法一般应具备时域分析和频谱分析两种测试处理和分析手段，并在长期定时定点检测的基础上进行。关于测点的选择，一般遵守轴承座附近是天然的最佳测点、重要部位的测点可以布置多、密一些、测点的选择要兼顾轴径向平面的水平与垂直两个方向和轴向方向、要在比较平坦的箱体表面布置测点、简易诊断的测点不宜过多等原则。所以，本文在齿轮箱不同部位的四个加速度传感器，收集了传感器统计到的五种不同状态下的振动信号数据，并且对五个状态下的振动信号时间序列数据进行分析，绘制时间序列函数，并提取相关特征。通过对数据提取平均值、方差、峰度和偏度这些对判断齿轮箱齿轮故障有着重要作用的特征变量。对每一组数据进行特征数据计算，通过特征数据计算对这些变量进行了基于组合赋权的IDP-CRUTIC的评价模型进行有效性分析，检测特征是否能有效描述齿轮箱故障。本文采取的模型并非只是通常使用的独立性评价模型，而是通过对一组数据进行不同方式的评价方法，例如本文选择了主观加权、客观加权、总体加权三种加权方式，对三种方式按照效果优劣进行指标赋权。通过不同的算法对得到的数据进行组合，获得最后的特征权重，最后进行分析。

2. 基本理论

2.1. 平均值

平均值作为函数中一个重要的统计学特征，着重反映着每一组数据的总体走势，以及各组数据的总体水平，其计算公式如下：

$Averag{e}_{ik}=\frac{{\displaystyle {\sum }_{j=1}^n{T}_i^j}}{n}$ (1)

2.2. 方差

标准差作为离散数学的一个重要特征，在概率统计中最常使用作为统计分布程度上的测量依据，其能着重反映一个数据组的离散程度。其计算公式如下：

$Va{r}_{ik}=\frac{{\displaystyle {\sum }_{j=1}^n{\left(T_i^j-Averag{e}_i\right)}^2}}{n}$ (2)

2.3. 峰度

峰度是表征概率密度分布曲线在平均值处峰值高低的特征数。样本的峰度是和正态分布相比较而言统计量，在统计学中，峰度衡量实数随机变量概率分布的峰态。其对统计振动信号的差异性起着重要的作用。其计算公式为：

$ske{w}_{ik}=\frac{\frac{1}{n}{\displaystyle {\sum }_{j=1}^n{\left(T_i^j-Averag{e}_i\right)}^3}}{{\left[\frac{1}{n-1}{\displaystyle {\sum }_{j=1}^n{\left(T_i^j-Averag{e}_i\right)}^2}\right]}^{3/2}}$ (3)

2.4. 偏度

偏度是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。其是统计数据分布偏斜方向和程度的度量与非对称程度的数字特征。其计算公式为：

$kur{t}_{ik}=\frac{\frac{1}{n}{\displaystyle {\sum }_{j=1}^n{\left(T_i^j-Averag{e}_i\right)}^4}}{{\left[\frac{1}{n}{\displaystyle {\sum }_{j=1}^n{\left(T_i^j-Averag{e}_i\right)}^2}\right]}^2}-3$ (4)

2.5. 标准差

标准差在概率统计中通常作为统计分布程度上的测量，反映的是组内个体间的离散程度。标准差的定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根。其计算公式为：

$\sigma =\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(x_i-\mu \right)}^2}}{n}}$ (5)

2.6. 变异系数

当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差较大，或者量纲不一致，无法直接使用标准差进行比较时，变异系数可以做到消除测量尺度和量纲的影响。其定义为标准差与平均数的比。其数据大小不仅受变量值离散程度的影响，而且还受变量值平均水平大小的影响。根据式(5)和式(1)的比，其计算公式为：

$c_v=\frac{\sigma }{\mu }$ (6)

3. 仿真分析

3.1. 数据处理

模拟数据统计了各个部位传感器的振动数据，本文通过实验得到的数据，刻画振动幅度时间序列的变化。传感器采样频率为6.4 kHz，下列为部分实验得到的数据(见表1~5，其中， $senso{r}_i$ 中i表示第i个加速度传感器， $i=1,2,3,4$ )。

Table 1. Selected vibration signals collected under normal operating conditions of the gearbox

表1. 齿轮箱正常工况下采集到的部分振动信号

Table 2. Selected vibration signals collected in fault state 1

表2. 故障状态1下采集到的部分振动信号

Table 3. Selected vibration signals collected in fault state 2

表3. 故障状态2下采集到的部分振动信号

Table 4. Selected vibration signals collected in fault state 3

表4. 故障状态3下采集到的部分振动信号

Table 5. Selected vibration signals collected in fault state 4

表5. 故障状态4下采集到的部分振动信号

基于公式(1)可以得出中间数据间隔t，使用SPSSPRO软件分别绘制四个部位的振动信号时间序列图，从中观察时间序列的变化情况。

针对五个状态内分别四个部位时间序列变化图进行分析，可以看出，所有状态、所有部位的振动信号时间序列均为平稳的时间序列数据，且短时间内波动性较弱，具有一定的规律性。

如图为四个sensor的五个状态的分布散点图。下面图1~4中的横坐标和纵坐标均分别表示的是序号和振动信号的值。

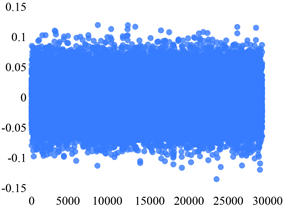
Sensor 1正常状态

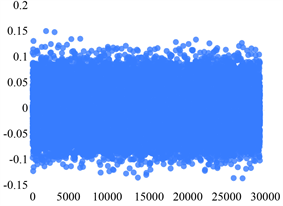
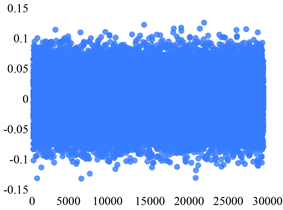Sensor 1故障状态1Sensor 1故障状态2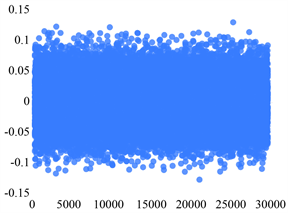 Sensor 1故障状态3Sensor 1故障状态4

Figure 1. Scatter plot of the distribution of the five states of Sensor 1

图1. Sensor 1五个状态的分布散点图

Sensor 2正常状态

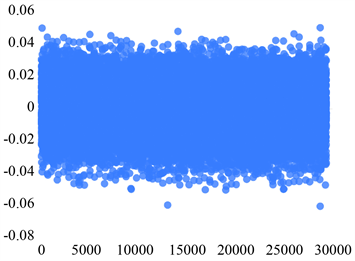
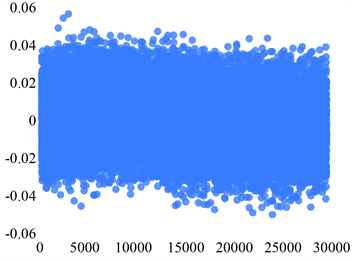Sensor 2故障状态1Sensor 2故障状态2 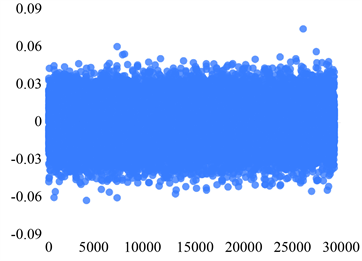Sensor 2故障状态3 Sensor 2故障状态4

Figure 2. Scatter plot of the distribution of the five states of Sensor 2

图2. Sensor 2五个状态的分布散点图

通过对上述不同部位振动信号时间序列的简单分析，可以从如下几个方面对其特征进行提取：

1) 传感器振动信号序列的平稳程度；

2) 传感器振动信号序列的局部波动程度；

3) 传感器振动信号序列前后的相关性；

4) 传感器时间序列的统计特征。

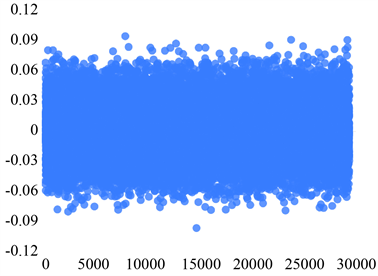
Sensor 3正常状态

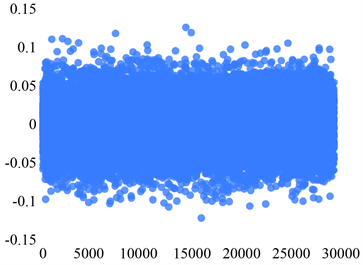
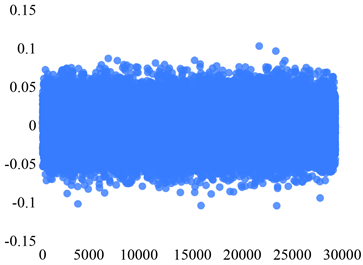Sensor 3故障状态1Sensor 3故障状态2 Sensor 3故障状态3Sensor 3故障状态4

Figure 3. Scatter plot of the distribution of the five states of Sensor 3

图3. Sensor 3五个状态的分布散点图

Sensor 4正常状态

Sensor 4故障状态1 Sensor 4故障状态2 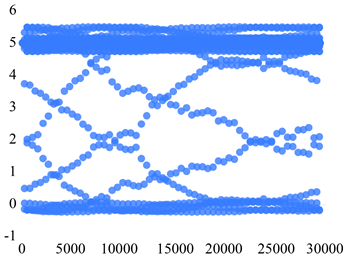Sensor 4故障状态3 Sensor 4故障状态4

Figure 4. Scatter plot of the distribution of the five states of Sensor 4

图4. Sensor 4五个状态的分布散点图

3.2. 特征计算

根据上述式(1)~(6)，使用SPSSPRO计算得到如下结果：

从计算结果可以看出，除了样本量特征以外，各个部位各个状态各特征之间均存在差异性，表明特征的选取具有一定的有效性，为了进一步检验特征的有效性选择其他系数进行分析(见表6~9)：包括但不限于变异性系数分析、独立性权系数法、CRUTIC指标权重系数分析。

Table 6. Calculation results of Sensor 1 related features

表6. Sensor 1相关特征计算结果

Table 7. Calculated results of Sensor 2 correlation features

表7. Sensor 2相关特征计算结果

Table 8. Calculation results of Sensor 3 related features

表8. Sensor 3相关特征计算结果

Table 9. Calculated results of Sensor 4 related features

表9. Sensor 4相关特征计算结果

3.3. 基于组合赋权的IDP-CRUTIC的评价模型

评价模型在金融、旅游等行业都有广泛的应用。评价模型往往通过分析各个对象特征之间的数值关系，并通过各个特征的权重，对每个对象进行评分，帮助决策者进行决策。传统的评价模型有独立性(IDP)评价模型、多选相关性(CRUTIC)评价模型等。评价IDP模型能很好地处理数据之间的关系，从而较准确地对各个对象进行评级。但其仍存在着无法确定方案的发展趋势的缺点。CRUTIC评价模型通过考虑各个对象之间的相似程度进行评分，但无法衡量各对象与最优值之间的关系。并且，大部分的评价模型对于特征的权重选取一般采用专家分析，过于主观。基于此，本文提出了一种基于组合赋权的IDP-CRUTICC评价模型。

综上所述，绘制模型的构建流程图(见图5)：

Figure 5. Flowchart of IDP-CRUTIC evaluation model based on portfolio assignment

图5. 基于组合赋权的IDP-CRUTIC评价模型流程图

4. 实验

4.1. 独立性评价模型

特征有效性分析和变异性系数的分析——在概率论和统计学中，变异系数是概率分布离散程度的一个归一化量度，其计算公式如下：

$C_v=\left(SD÷MN\right)\times 100\%$ (7)

其中， $c_v=\frac{\sigma }{\mu }$ 。

变异系数只在平均值不为零时有定义，而且一般适用于平均值大于零的情况。因此在比较两组量纲不同或均值不同的数据时，应该用变异系数而不是标准差来作为比较的参考(其中， $senso{r}_{ij}$ 表示第i中状态下的第j个加速度传感器， $i=0,1,2,3,4$ ； $j=1,2,3,4$ )。

Table 10. Mean, variance, coefficient of variation and weight values for each group of data

表10. 各组数据平均值，方差，变异性系数及权重数值

上表展示了变异系数法的权重计算结果，由上表的结果对各个指标的权重进行分析(见表10)。

1) 指标变异性为标准差，标准差越大则权重越大；

2) 变异系数是通过变异指标中的全距、平均差或标准差与平均数对比得到的；

3) 权重是信息量的归一化。

由于直方图可以适用于任何情况，且更加直观易懂，在本文中不需要详细的数据表示，所以将上表的数据转化为直方图如下图所示。图6中的纵坐标表示加速度传感器在变异系数的计算方式下按照权重大小的排序，横坐标表示该加速度传感器的权重，即重要程度。

Figure 6. Histogram of importance of coefficient of variation CV index

图6. 变异系数CV指标重要度直方图

独立性权系数法的思想在于根据各指标与其他指标之间的共线性强弱来确定指标权重的，若指标之间的共线性关系越强，越容易由其他指标的线性组合表示，重复信息越多，因此该指标的权重也就应该越小。即若指标 $x_k$ 与其他指标的复相关系数R越大，该指标的权重越小。其中，

$R=\frac{{{\displaystyle \sum }}^{\text{}}\left(y-\bar{y}\right)\left(\hat{y}-\bar{y}\right)}{\sqrt{{{\displaystyle \sum }}^{\text{}}{\left(y-\bar{y}\right)}^2{{\displaystyle \sum }}^{\text{}}{\left(\hat{y}-\bar{y}\right)}^2}}$ (8)

Table 11. Independence weight coefficient method to calculate each group of data

表11. 独立性权系数法计算各组数据

独立性权系数法只考虑了数据之间相关性，其计算方式是使用回归分析得到的复相关系数R 值来表示相关性强弱，值越大说明共线性越强，权重会越低。上表展示了独立性权系数法的权重计算结果(见表11)，根据结果对各个指标的权重进行分析。

1) 复相关系数R值越大说明重复信息越多，权重则越小；

2) 复相关系数1/R值越大，则说明权重应该越大；

3) 权重由复相关系数倒数1/R值归一化得到。

由于直方图可以适用于任何情况，且更加直观易懂，在本文中不需要详细的数据表示，所以将上表的数据转化为直方图如下图所示。图7中的纵坐标表示加速度传感器在独立性权系数的计算方式下按照权重大小的排序，横坐标表示该加速度传感器的重要度。

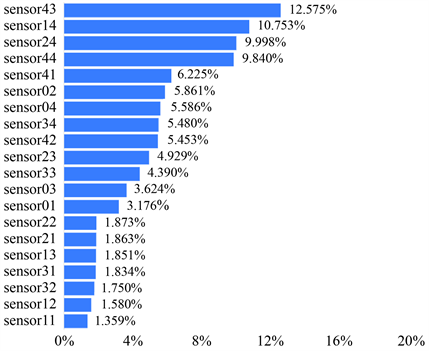
Figure 7. Histogram of the importance of indicators by the independence weight coefficient method

图7. 独立性权系数法指标重要度直方图

上图以直方图形式展示了指标的重要度排序(见图7)。

利用数据的波动性或者数据之间的相关关系情况进行权重计算——对比强度和冲突性指标，标准差越大权重越高，相关系数值越大权重越低，分析的指标或因素之间有一定的关联关系，且数据具有稳定性。

4.2. 多选相关性评价模型 [8]

CRITIC权重法是基于评价指标的对比强度和指标之间冲突性来衡量指标的客观权重，在考虑指标变异性大小的同时兼顾指标之间的相关性。通过指标的标准差 $\sigma$ 反映指标的变异性，标准差越大差异越大，对应指标包含的信息也越多，应该分配更多的权重。指标冲突性用相关系数表示，其计算公式为

$r_v=\underset{i=1}{\overset{m}{{\displaystyle \sum }}}\left(1-r_{iv}\right)$ (9)

其中， $r_v$ 为指标v与其他指标的冲突性，相关性越强值越小，分配的权重越低。 $r_{iv}$ 为指标的i、v的相关性系数，i、v分别为不同的评级指标索引。

通过变异性和冲突性可计算信息量 $c_v={\sigma }_v\times r_v$ ，各个信用评级指标的权重可由下式计算得到

$w_v=\frac{c_j}{{\displaystyle {\sum }_{i=1}^m{c}_j}}$ (10)

上表展示了CRUTIC法的权重计算结果(见表12)，根据结果对各个指标的权重进行分析。

1) 指标变异性为标准差，标准差越大则权重越大；

2) 冲突性为相关系数，指标之间相关性越强则冲突性较低，权重越小；

3) 信息量为指标变异性*冲突性指标；

4) 权重是信息量的归一化。

Table 12. Calculation results of weights of CRUTIC method

表12. CRUTIC法的权重计算结果

由于直方图可以适用于任何情况，且更加直观易懂，在本文中不需要详细的数据表示，所以将上表的数据转化为直方图如下图所示。图8中的纵坐标表示加速度传感器在CRUTIC指标重要度的计算方式下按照权重大小的排序，横坐标表示该加速度传感器的重要度。

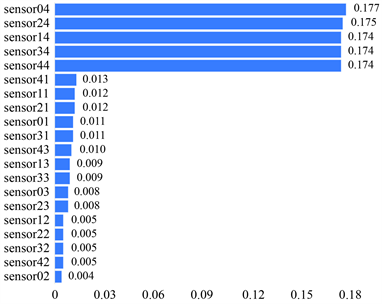
Figure 8. Histogram of importance of CRUTIC indicators

图8. CRUTIC指标重要度直方图

5. 结论

通过上述实验，可以计算出各自的权重，如下表13所示(其中，第一行表示IDP计算出的权重，第二行表示CRUTIC计算出的权重，第三行表示组合赋权IDP-CRUTIC的总权重)。

Table 13. Calculation of sum weights

表13. 总和权重计算

最终结果分析：

通过上述模型建立与指标选取，通过比较可以得知sensor4即第四个加速度传感器所在的部位上的综合指标权重较大，且在散点图中，仅有sensor4的时间序列分布图呈现规律性，变异系数CV分析中仅有sensor4中为零，即变异概率低：可见sensor4的数据最能看出是否故障。

由于直方图可以适用于任何情况，且更加直观易懂，在本文中不需要详细的数据表示，所以将上表的数据转化为直方图如下图9所示。

Figure 9. Weighting of integrated indicators

图9. 综合指标权重

由上述可知，基于组合赋权的IDP-CRUTIC的评价模型可以很好地选择出评价齿轮箱故障的部分。考虑到不同评价模型的差异性和各自的优点，基于组合赋权的IDP-CRUTIC模型可以避免一些模型的不足，扬长自身的优点，通过融合权重能获得符合数值标称意义的权重结果。该模型还综合了主观特性和客观属性 [9] ，能较好地实现对齿轮箱故障的评估，而且进行了单项能力和综合效能比对，更加有利于帮助决策者对齿轮箱故障的选取、排查和及时处理，具有较强的可操作性和推广价值。

NOTES

^*通讯作者。