1. 引言
车轮磨损预测一直是当前铁路研究领域的一个关键课题,因为它是列车行车安全性和铁路运营效率性的核心,车轮的过度磨损不仅会导致车轮破损甚至列车脱轨等严重事故,从而影响列车的安全性,而且车轮的更换和返厂修理也会影响列车的运行效率和出勤率。通过对车轮磨耗数据的预测,我们可以准确把握车轮的磨损情况,及时对车轮进行镟修或更换,确保列车的行车安全。车轮磨耗的预测一般分为两种 [1] :基于动力学的磨耗预测,或基于大数据技术进行磨耗预测。
2. 预测模型
2.1. 遗传算法优化支持向量机原理
支持向量机(Support vector machine,简称SVM)由Vapnik [2] 提出,是一种广泛应用于模式识别、机器学习以及数据挖掘领域的算法,它基于统计学习的思路,通过构建最优的超平面来解决分类问题。而目前来说,核函数可以将点映射到高维,将原问题转化为凸二次规划问题,求解目标函数可以获得全局最优解,从而提高SVM的性能。应优化的参数包括:惩罚参数C和核函数参数g,松弛变量等。由于参数空间较大且过度拟合等问题的存在,SVM参数的调优一直是一个具有挑战性的热门课题。SVM通常分为SVC (识别分类)和SVR (回归预测)两种,本文使用的方法为回归预测。
遗传算法(genetic algorithm,简称GA) [3] - [9] 是一种优化算法,受到自然选择和遗传遗传机制的启发。它使用种群中的个体(基因组)来搜索问题的解决方案,通过选择、交叉和变异等操作来逐渐改进这些个体,以找到最佳解决方案。在GA-SVM中,GA被用来搜索SVM的参数,以改进SVM的性能。具体来说,GA-SVM的个体代表SVM的参数组合,包括核函数、惩罚参数等。初始种群中的个体是随机生成的。通过使用SVM对数据进行训练和验证,GA评估每个个体的性能,然后选择和进化最优的个体。进化过程包括选择、交叉和变异操作,以生成下一代的个体。迭代进行,直到找到适合解决问题的最佳参数组合。
本文选用径向基函数(radial basis functions, RBF)核函数为:
(1)
RBF核函数可以分析更高维度的数据,并且只需要定义两个参数C和g,且具有很好的收敛性,适合我们进行预测。
对于g的取值,不妨设两点的距离为
,
当
时,
,
(2)
当
时,
,
(3)
可以看出,g参数越大,可能会导致低偏差,高方差,分的类别会越细,但g过大可能导致超平面形状奇怪(例如梅花形),模型的鲁棒性变差;g参数越小,可能会导致低方差,高偏差,分的类别会越粗,导致无法将数据区分开来。
优点:GA-SVM可以用于寻找最佳的SVM参数组合,从而提高SVM的性能。它在复杂问题中有潜力,因为可以搜索大范围的参数空间。
2.2. 预测流程
在大数据技术对轮对数据进行数据提取和汇总的过程中,会提取到大量的轮对可观测数据,包括轮缘厚度、车轮直径、轮缘高度、踏面磨耗等。其中踏面磨耗 [10] 与机车状态密切相关且可以定期检测,是机务段检修工对轮对状态的主要考量标准之一,也成为许多机车状态监测和故障预警系统中的关键特征之一。
因而,在众多的轮对观测数据中,本文选取的最核心的车轮踏面磨耗量作为预测对象,数据来源为某型轮轨车轮轮对磨耗量的历史数据。也仅仅选用了踏面磨耗的数据,在大数据环境下,对于支持向量机模型来说,选用维度低的数据可以获得更高的计算速度,避免产生“核函数危机”,对车轮的数据进行选择,维度不能太多。
预测流程:
步骤1:数据处理:将数据进行标准化,使其具有零均值和单位方差。并划分训练集与测试集;
步骤2:目标函数设定为均方误差MSE,设置需要优化的支持向量机参数C和g,并设置参数的上下界,使其对数据进行回归预测;
步骤3:遗传算法参数设置:包括迭代次数、速度限制、和权重系数,以进行适应度计算;
步骤4:提取C和g的最佳参数组合进行支持向量机训练,方式为回归预测;
步骤5:设置循环,使用训练集最后一个数据的观测值,预测测试集第一个数据的取值;
步骤6:将数据去标准化,并对比预测数据和实际数据的曲线图,以及预测数据和实际数据之间的误差值;
步骤7:计算RMSE,MAPE,MAE,MSE的数值。
3. 预测结果
对于车轮磨耗的预测流程也采用上文中大数据技术,流程为:数据收集,去除脏数据,设置预测集,机器学习预测,分析结果。本次实验在Windows 10环境下使用MATLAB R2022a,对车轮磨耗数据进行仿真。
考虑到车轮镟修过程中会对车轮半径产生较大影响,本文在某型车轮的历史数据中,在同一镟修周期中共选择了140组历史数据样本,每组观测数据的间隔为6天,选取前112组作为训练数据样本,后28组作为测试数据样本。本次数据选用某型列车的单轮历史数据,总磨耗的观测数据为两年半以来的历史车轮磨耗数据,参数设置如表1所示。

Table 1. Upper and lower bounds on the values of parameters C and g
表1. 参数C和g的取值上下界
图1表示的为适应度的收敛过程,横坐标为迭代次数,纵坐标为适应度的值,注意此处的适应度为数据归一化后的适应度,该适应度的数值并非最终结果的数据。图2为实际数据与预测数据的对比图,横坐标为数据个数,纵坐标为车轮轮径磨耗速率,从结果图可以看出拟合效果较好。
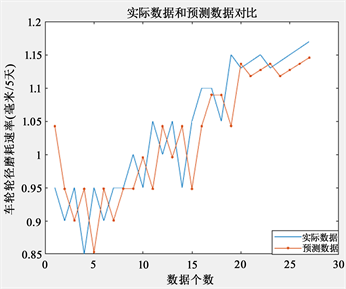
Figure 2. Comparison between actual data and predicted data
图2. 实际数据与预测数据对比
4. 对比与分析
本次数据选用某型列车的单轮历史磨耗数据,先使用前50%的数据对剩余数据进行回归预测,然后逐渐增加训练集的数量,因为模型不变,所以仅以RMSE作为评价标准横向对比。得到的结论是该模型随着基础数据数量的增大,预测的精度的增加,不同占比的训练集预测误差如表2所示,此处的RMSE值依然为归一化后的数据,与实际结果有差别,此处着重为了表达随着训练集增加,RMSE值逐渐减少。同时说明该模型的特点为:变量少,需要一定的基础数据,与灰色预测类算法的变量多,无需过多基础数据的特点正好相反。也说明在现实中需要尽可能多采集车轮磨耗数据。

Table 2. Comparison of RMSE predictions under different proportion test sets
表2. 不同比例测试集下预测RMSE对比
对于一个算法预测模型来说,各项误差是评价其实用性的关键,且误差的程度需要用多种评价数值综合考量,防止出现“高方差,低偏差”或“高偏差,低方差”等模型不平衡的现象,本节使用RMSE,MAPE,MAE,MSE四个指标进行评价,结果如表3所示。

Table 3. List of numerical evaluation indicators
表3. 数值评价指标表
同时,通过预测数据可以看出,在车轮轮径磨耗速率为1.05 mm/6天时,车轮磨损速度增长很快,而此时累积磨耗也较高,此时应对车轮进行镟修处理。
5. 结论
本文基于GA-SVM模型对车轮磨耗数据进行了预测,一定程度上保证了列车运营的安全,同时为镟修的时机提供有效的结论,从而避免因车轮损坏引起的安全事故和其他损失。此外,准确预测车轮磨耗还可以优化车辆维护计划,降低维护成本,提高车辆运营效率,为后续的车轮镟修方案和整车镟修提供参考。
同时我们得出以下结论:
(1) 增大数据集有利于提高预测精度,在训练数据和预测数据比例为8:2时,预测精度最高。
(2) GA-SVM数学模型能够有效地寻找到参数C和g的最佳组合。
基金项目
辽宁省教育厅科学研究项目(LJKZ0493);大连市科技创新基金应用基础研究项目(2022JJ12GX029)。