浅析x > 0，1 < a，(a + x)^a与a^{(a + x)}的大小关系

A Study of x > 0, with 1 < a, the Magnitude of (a + x)^a versus a^{(a + x)}

摘要: 通过构造重要函数，针对Nam，Kyumin在2023年提出的问题，给出新的直接证明。进一步，我们对问题进行了延展，得到了定性结果。

Abstract: By constructing important functions, for Nam, Kyumin’s problem in 2023, we give new direct proof. Further, we extend the problem and obtain qualitative results.

1. 引言

$\pi$ 和e作为数学中两个重要的无理数。比较 ${\pi }^e$ 和 $e^{\pi }$ 的大小是一个饶有兴趣的数学问题。众所周知，在不利用计算机近似估计的情况下，我们很难得到两者之间的大小关系。作者KYUMIN NAM在 [1] 中运用计算机得到了两者的近似值，不难看出，两者的值是十分接近的。超越数两者之间的大小比较大都采用的是计算机近似估计的方法。毫无例外 ${\pi }^e$ 和 $e^{\pi }$ 作为超越数比较大小的方法也是如此。然而，近似计算的验证方式本身粗糙的，于是，在比较超越数之间大小关系的研究中，使得结果更具有说服力，通过严格的分析论证以及直观的几何验证方式引起了一些学者的关注。出于这样的动机，本文重点研究基于 ${\pi }^e$ 和 $e^{\pi }$ 大小关系的结果，在一定范围内b^a和a^b的大小关系。不同于直接根据底数大小关系构造特殊函数的方式，文中通过引入幂指(方程)不等式这一框架，首先引入变量 对问题进行函数化，其次运用对数与指数之间的性质，在一定范围内，将问题转化为一次函数与对数函数在取定变量x时的大小关系。

1987年，Fouad，Nakhli [2] 通过严格的数学证明得到了 ${\pi }^e$ 和 $e^{\pi }$ 的大小。在此基础上2019年，Bikash，Chakraborty [3] 借助特殊函数图像，给出了更为直观的验证结果。进一步类似的，2020年，Haque，Nazrul [4] 构造了特定函数，将结果进行了延展，得到了当 $e<A$ 时， $e^A<A^e$ 的结果。其中 ${\pi }^e$ 和 $e^{\pi }$ 为该结果下的特殊情形。2022年，Nam，Kyumin [5] 在Haque，Nazrul [3] 的结果下，构造了新的函数，给出了新的验证方式，得到了同样的结果。2023年，Nam，Kyumin [1] 在2022年的结果上，再次进行拓展，得到了更加宽泛的结论，即， $e<a<b\Rightarrow b^a<a^b$ 。

本文主要安排如下，第一，我们构造了关键函数并利用微分学理论，在 [1] 的结论上，得到了更为简便的证明方式，当 $e<a<b$ 时， ${\left(a+x\right)}^a<a^{\left(a+x\right)}$ 。第二，我们在上述的结论下，进行了推广，当 $1<a<e$ 时，得到了 ${\left(a+x\right)}^a$ 与 $a^{\left(a+x\right)}$ 的大小关系存在三种情形。在文章的最后，我们给出两个例子说明结论在该幂指方程解的存在性分析的应用。

2. 主要结果

首先，我们引入关键函数 $f\left(x\right)$ 和 $g\left(x\right)$ 给出了严格的分析论证，得到文献 [1] 中同样的结论，同时，给出了直观的几何图像验证。

定理1 对所有实数 $x>0,e\le a$ ，有 ${\left(a+x\right)}^a<a^{\left(a+x\right)}$ 。

证明：考虑关键函数

$f\left(x\right)=\frac{x}{a},g\left(x\right)={\log }_a\left(x+a\right)-1$ (1)

令

$h\left(x\right)=f\left(x\right)-g\left(x\right)=\frac{x}{a}-\left[{\log }_a\left(x+a\right)-1\right]\forall a\ge e,x>0,$ (2)

有

$h^{\prime }\left(x\right)=\frac{1}{a}-\frac{1}{\left(x+a\right)\ln a}=\frac{\left(x+a\right)\ln a-a}{a\left(x+a\right)\ln a},$ (3)

容易验证，当 $a\ge e,x>0$ 时， $h^{\prime }\left(x\right)>0$ ，从而 $h\left(x\right)$ 在定义域中是严格单调增加的。由于 $h\left(0\right)=0$ ，于是可以得到 $f\left(x\right)>g\left(x\right)$ ， $\forall a\ge e,x>0$ ，即，

$\begin{array}{l}{\log }_a\left(x+a\right)-1<\frac{x}{a}\iff {\log }_a\left(x+a\right)<\frac{a+x}{a}\\ \iff {\log }_a{\left(x+a\right)}^a<x+a\\ \iff {\left(a+x\right)}^a<a^{\left(x+a\right)}\forall a\ge e,x>0\end{array}$ (*)

通过 $(\ast )$ 式的等价结果，我们可以从如图1中得到直观的验证，

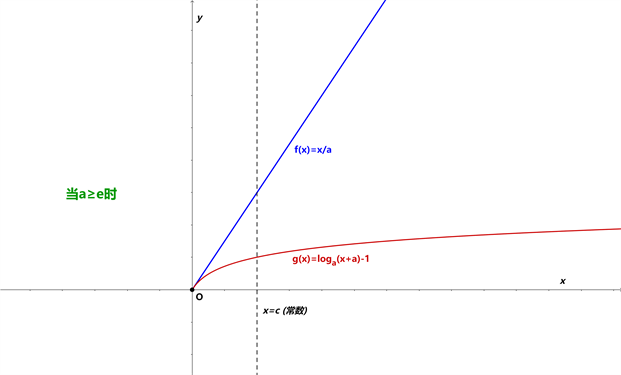
Figure 1. For any $a\ge e$ , $x>0$ , $f\left(x\right)$ , $g\left(x\right)$ image

图1. 对任意的 $a\ge e$ ， $x>0$ 时， $f\left(x\right)$ ， $g\left(x\right)$ 图像

证毕！

下面我们给出一些推论。

令 $b=a+x$ 。

推论1 [1] 对于任意的实数a，b且 $e\le a<b$ ， $b^a<a^b$ 。

令 $a=e$ 。

推论2 [2] [3] 对于任意的实数 $b>e$ ， $b^e<e^b$ 。

令 $a=e$ ， $x=\pi -e$ 。

推论3 [4] [5] ${\pi }^e<e^{\pi }$ 。

接下来，在幂指(方程)不等式框架下，我们利用关键函数 $f\left(x\right)$ 和 $g\left(x\right)$ 对研究问题进行延展，考虑当 $x>0,1<a<e$ 时， ${\left(a+x\right)}^a$ 与 $a^{\left(a+x\right)}$ 的大小关系。

定理2 对于任意常数a，满足 $1<a<e$ ，则存在唯一的常数 $m_a>0$ ，

(i) 当 $x>m_a$ ， ${\left(a+x\right)}^a<a^{\left(a+x\right)}$ ，

(ii) 当 $x=m_a$ ， ${\left(a+x\right)}^a=a^{\left(a+x\right)}$ ，

(iii) 当 $0<x<m_a$ ， ${\left(a+x\right)}^a>a^{\left(a+x\right)}$ 。

证明：已知 $1<a<e$ ，令 $h^{\prime }\left(x\right)=0$ ，则有

$x=\frac{a}{\ln a}\left(1-\ln a\right)>0.$

因此，当 $x<\frac{a}{\ln a}\left(1-\ln a\right)$ 时， $h\left(x\right)$ 严格单调递减，当 $x>\frac{a}{\ln a}\left(1-\ln a\right)$ 时， $h\left(x\right)$ 严格单调递增。

将 $x=\frac{a}{\ln a}\left(1-\ln a\right)$ 代入(2)，则有

$\begin{array}{c}h\left(\frac{a}{\ln a}\left(1-\ln a\right)\right)=\frac{\frac{a}{\ln a}\left(1-\ln a\right)}{a}-\left[{\log }_a\left(\frac{a}{\ln a}\left(1-\ln a\right)+a\right)-1\right]\\ =\frac{1}{\ln a}-{\log }_a\frac{a}{\ln a}=\frac{1}{\ln a}-\left({\log }_{a}a-{\log }_a\ln a\right)\\ =\frac{1}{\ln a}-1+{\log }_a\ln a=\frac{1}{\ln a}-1+\frac{\ln \left(\ln a\right)}{\ln a}\\ =\frac{1+\ln \left(\ln a\right)-\ln a}{\ln a},\end{array}$

因为 $1<a<e$ ，则 $0<\ln a<1$ 。设 $k\left(y\right)=1+\ln y-y$ ， $0<y<1$ ，从而

$k^{\prime }\left(y\right)=\frac{1}{y}-1>0,$

即， $k\left(y\right)$ 是严格单调递增的，于是

$\underset{0<y<1}{\sup }k\left(y\right)=\underset{y\to 1-}{\lim }\left(1+\ln y-y\right)=0.$

通过上面的证明，可得

$h\left(\frac{a}{\ln a}\left(1-\ln a\right)\right)<0.$

固定常数 $1<a<e$ ，计算下面公式可知

$\underset{x\to +\infty }{\lim }\frac{{\log }_a\left(x+a\right)}{\frac{x+a}{a}}=a\cdot \underset{x\to +\infty }{\lim }\frac{{\log }_a\left(x+a\right)}{x+a}=0,$ (4)

于是，有

$\underset{x\to +\infty }{\lim }h\left(x\right)=\underset{x\to +\infty }{\lim }\left\{\frac{x}{a}-\left[{\log }_a\left(x+a\right)-1\right]\right\}=+\infty ,\forall a>1$

根据根的存在性定理，可以得到存在唯一常数 $m_a>\frac{a}{\ln a}\left(1-\ln a\right)$ ，使得 $h\left(m_a\right)=0$ 。

通过上述对 $h\left(x\right)$ 的分析结果，我们绘制了关于 $f\left(x\right)$ 和 $g\left(x\right)$ 的函数图像。再结合 $(\ast )$ 式的等价结果。于是，可以从如图2中得到该定理的直观验证，

Figure 2. $f\left(x\right)$ , $g\left(x\right)$ image

图2. $f\left(x\right)$ ， $g\left(x\right)$ 图像

证毕。

注：容易发现，虽然定理2的出发角度是比较幂(指)数之间的大小，但结论却可以用作关于幂指方程 ${\left(a+x\right)}^a=a^{\left(a+x\right)}$ ，在某限定条件下的解的存在性分析。特别地，在大量无法求解的指数方程过程中，常常通过计算机采用迭代近似逼近的方式去求得近似解，却往往忽略了首先需要验证解的存在性。因此，定理2在所给定的限制条件下给出了该幂指方程的解的存在性是具有意义的。

下面，通过定理1，2的结论给出两个例子。

例1 问幂指方程 ${\left(3.2+x\right)}^{3.2}={3.2}^{\left(3.2+x\right)}$ 是否有非负实数解，有几个？

解：因为 $3.2\ge e$ ，所以由定理1的结论，直接得到该方程无正实数解。又因为 $x=0$ 时，方程恒成立，所以该方程存在非负实数解，且解为 $x=0$ 仅有1个。

例2 问幂指方程 ${\left(\sqrt{2}+x\right)}^{\sqrt{2}}={\sqrt{2}}^{\left(\sqrt{2}+x\right)}$ 是否有非负实数解，有几个？

解：已知 $1<\sqrt{2}<e$ ，所以由定理2的结论，直接得到该方程有且仅有唯一正数解。又因为 $x=0$ 时，方程恒成立，所以该方程存在非负实数解，有两个。