1. 引言
随着全球气候变化和环境问题日益严重,新能源汽车已成为汽车产业发展的必然趋势。作为新能源汽车的重要组成部分,电动汽车因其零排放、低能耗和高性能等优点,逐渐受到消费者的青睐。锂离子动力电池具有能量密度和功率密度高、循环寿命长、自放电倍率小以及对环境友好等特点 [1] ,因而被广泛地用作电动汽车的驱动部件。但是随着充放电循环地进行,电池的容量也会逐渐衰减,最终带来的后果是续航里程减少,功率衰减,甚至引发安全事故。所以电池容量的准确估计对于其性能和安全性具有至关重要的作用 [2] 。因此,对电池容量进行估计研究具有重要的实际意义。
目前,锂离子动力电池容量估计的主流方法大致可以分为基于经验模型的方法与基于数据驱动的方法两大类 [3] 。基于经验模型的方法包含了电化学模型,机理模型、等效电路模型等具有明确参数的数理化模型 [4] ;而基于数据驱动的方法则是从数据角度出发,通过大数据驱动,再结合算法来实现基于数据输入和容量输出响应。两种方法各有优劣,基于经验模型进行容量估计的方法模型简单,计算量较小,但是经验模型是开环模型,所以在进行容量估计时容易出现参数失配的问题 [5] 。基于数据驱动的容量估计方法无需考虑电池的衰减机理,可以实现容量的闭环估计,但是只可以进行当前状态的容量估计,无法实现实时预测。结合这样的背景,本文的容量融合估计方法考虑将二者相结合,建立容量融合估计模型,使两种容量估计方法各自取长补短,在提高容量估计精度的同时实现连续预测。
综上所述,为了提高容量估计的精度和鲁棒性,本文基于Simulink仿真平台搭建容量融合估计模型。该模型将容量在线辨识得到的结果作为阿伦尼乌斯模型的输入,通过两个卡尔曼滤波分别进行模型参数的修正和容量的更新。与传统的基于经验模型或者数据驱动算法的容量估计方法相比,该模型融合了两种容量估计方法的长处,在保证估计精度与鲁棒性的同时也实现了容量的连续估计,具有一定的研究和应用价值。
2. 容量老化数据提取
为了实现融合估计的目标,本节需要为融合估计模型的验证和精度检验提供数据支持。然而电池的循环老化是一个漫长的过程,考虑到其时间周期较长,所以本文选用公开的NASA电池老化数据集作为模型验证的数据输入,通过NASA数据来验证该模型的可行性以及计算精度,减少实验的时间和成本。
NASA数据包含了不同温度下的电池老化试验数据,而本文选取了一款三元锂电池。这款电池进行了循环老化试验,同时记录每次循环后通过标准容量测试得到的容量实测值。电池的基本性能如表1所示。

Table 1. Standard test system result data
表1. 标准试验系统结果数据
3. 融合估计建模的建立
3.1. SOC–电量增益法在线估计
SOC–电量增益方法是基于充放电电量变化与对荷电状态(SOC, State of charge)变化之比,如式(1),SOC与电池容量可以由方程联系起来 [6] :
(1)
SOC–电量增益法在线估计电池容量的原理是基于电池的放电曲线和电压恢复曲线来进行容量估计。当电池在放电的过程中,随着放电深度的增加,电池的电压将逐渐降低。当电池放电深度达到一定程度时,电池的电压将会迅速降低到放电截止电压。在充电的过程当中,随着充电深度的增加,电池的电压也会逐渐升高,当电池的充电深度达到一定程度时,电池的电压将会迅速上升到充电截止电压。SOC–电量增益法在线估计主要是根据电池放电曲线和电压恢复曲线的特点,选取两个具有代表性的点,一个代表放电过程中的最低电压点,另一个代表充电过程中的最高电压点。随后根据这两个点的电压和电流值,利用公式计算出电池的容量。SOC–电量增益计算公式如式(2)所示:
 (2)
(2)
SOC–电量增益法主要通过充放电电量变化与对应SOC变化之比计算容量,式中,SOC(t1)为t1时刻电池荷电状态,SOC(t2)为t2时刻电池荷电状态,I(t)为t时刻电池电流,η为库伦效率(一般η ≈ 1),3600是将秒换算成小时的因数。
充放电电量变化普遍采用电量积分法,所以此类方法的区别实质是对应时间段SOC的不同获得方法。作为一个间接量,SOC不能直接被测量,大都是使用估计算法通过对状态参数的估计直接或间接得到。目前的主流技术路线有:安时积分法、开路电压法、基于现代控制理论的最优估计方法等 [7] 。
通过间接估计SOC,进一步选取两个不同的SOC点进行容量估计,理论上两个不同时刻的点可以任意选取,但是由于电池在充电过程当中电量累计计算与SOC估计均会存在误差,所以一般选取SOC相差较大的时刻点,目前通常选取SOC为20%和90%作为两个不同的时刻点进行容量估计,但该方法只能尽可能地减小误差,存在着一定的随意性,这也是该方法目前存在的缺陷。另外,SOC–电量增益法的估计结果可能会因为电池老化、温度等因素而有所偏差。所以为了更准确地估计电池容量,本文将SOC–电量增益法所得到的容量估计结果作为融合估计模型的一个输入,后续在融合估计模型的修正下,容量估计精度会有进一步的提升。
3.2. 阿伦尼乌斯容量衰减模型
3.2.1. 阿伦尼乌斯模型介绍
由于SOC–电量增益法的估计结果可能会因为电池实际工况的不同而产生较大误差,所以在SOC–电量增益法的基础上引入经验模型。经验模型可以通过拟合大量实验数据来标定模型参数,以此来实现容量的预测。其中比较常见的是阿伦尼乌斯(Arrhenius)公式对随着电池充放电循环而变化的容量进行拟合。阿伦尼乌斯容量衰减模型是一个描述化学反应速率常数与温度关系的经验公式。该模型由瑞典化学家阿伦尼乌斯在1889年提出,是加速寿命试验中常用的加速模型之一。Arrhenius方程标准形式如式(3)。Bloom等人 [8] 通过大量的电池衰减影响因素实验,分析了不同温度下电池衰减率的情况,在标准形式的基础上提出了如式(4)的容量衰减模型:
(3)
(4)
式中:A为大于零的常数;Ea代表反应的活化能,单位为J/mol;温度T的单位为K;R = 8.314 J/(mol∙K),R代表理想气体常数;t指时间,z指时间指数。其中A、Ea/R、z可以根据电池耐久性测试结果拟合得到。
3.2.2. 离散Arrhenius模型的建立
Arrhenius模型作为常用的容量衰减模型,适用于在基于SOC–电量增益法的基础上拟合容量衰减曲线。容量衰减模型如式(5)。
(5)
式中:ξ(s)为电池循环s次后的容量衰减量,A、Ea、R与式(4)含义相同,z为指数。一般将Ea/R视为整体,参数A、Ea/R、z可以通过实验室数据拟合获得。式(5)通常适用于稳态情况,以此基础上可以构建变温度工况下的Arrhenius容量衰减模型:
(6)
将式(6)左右对s进行求导得:
(7)
将式(6)代入式(7)得到消除s的微分形式:
(8)
将式(8)离散化处理:
(9)
式中,a1、a2、a3分别为:
(10)
通过式(9)迭代计算得到电池循环s次后相对容量衰减量,进一步转换得到Arrhenius模型容量估计结果:
(11)
其中C0指电池初始状态下的容量值,CA(s)指电池循环s次后的模型预测容量值。
3.3. 卡尔曼滤波融合估计模型
3.3.1. 融合估计框架建立
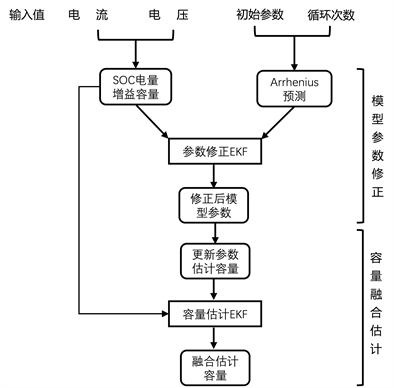
Figure 1. Schematic diagram of fusion estimation based on dual Kalman filtering
图1. 基于双卡尔曼滤波的融合估计原理图
SOC–电量增益法在阿伦尼乌斯模型的拟合下可以得到容量衰减曲线,但是经验模型在拟合曲线的工程中出现参数失配的问题,这也是经验模型的缺陷,针对这一问题,该部分采用两个独立的卡尔曼滤波,其中第一个卡尔曼滤波用来对Arrhenius模型的三个参数进行修正,第二个卡尔曼滤波使用修正后的参数对电池的容量进行融合估计。如图1所示,首先根据电池充放电的电流和电压在线计算SOC–电量增益法的容量值,根据电池的充放电循环次数和模型的初始参数初步拟合容量衰减曲线,进一步将Arrhenius模型与SOC–电量增益法所得的容量差值反馈给第一个卡尔曼滤波,利用第一个卡尔曼滤波的增益进行参数矫正。随后将修正后的模型参数再次输入到Arrhenius模型当中再次与容量在线估计的结果做差,利用第二个卡尔曼增益得到修正后的融合容量值,也就是最终的融合估计值。通过这种方式实现了基于数据驱动和经验模型的容量融合估计。
3.3.2. 基于卡尔曼滤波的容量估计
由于实车场景会实时发生变化,直接使用模型初始标定参数进行容量估计会产生模型参数失配的问题,因此引入两个卡尔曼滤波,分别进行模型参数实时修正和容量的融合估计。通过定期对模型参数进行更新,以提高容量估计的精度。
基于以上分析,引入卡尔曼滤波容量估计的状态空间方程:
(12)
初始化:
(13)
 (14)
(14)
迭代更新,当 状态向量时间更新:
状态向量时间更新:
(15)
误差协方差时间更新:
 (16)
(16)
卡尔曼增益:
 (17)
(17)
状态向量测量更新:
(18)
误差协方差测量更新:
 (19)
(19)
3.3.3. Simulink模型建立
基于Matla的Simulink仿真平台最终搭建的动力电池容量融合估计模型如图2所示,其中基于电池数据仿真模型的运行保证电池容量实时输出,同时还可以对Arrhenius模型的三个参数进行实时采集和监控。
模型搭建过程中,将电池真实容量值、容量在线辨识值、电池充放电循环次数、Arrhenius模型三参数分别作为模型的输入,Arrhenius模型初步根据容量在线辨识值拟合容量衰减曲线,随后采用两个独立的卡尔曼滤波,分别进行参数修正和容量融合估计。通过Simulink仿真平台将Arrhenius模型和卡尔曼滤波封装为独立模块,其中算法封装模块如图3所示。
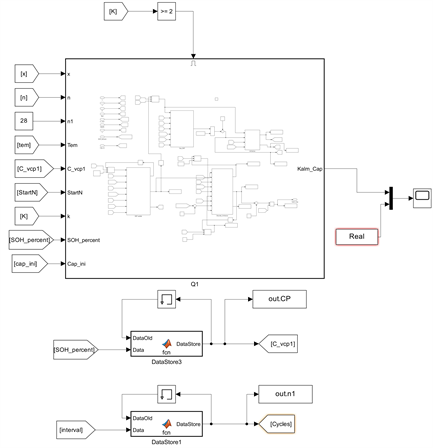
Figure 2. Capacity fusion estimation model
图2. 容量融合估计模型
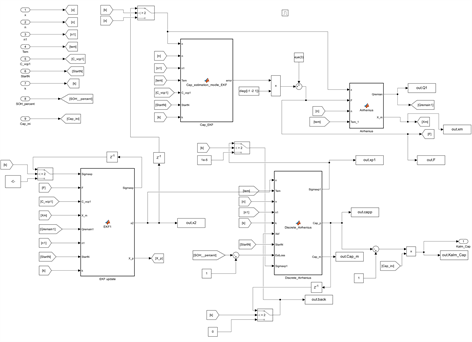
Figure 3. Dual Kalman filtering packaging module
图3. 双卡尔曼滤波封装模块
4. 结果
图4展示了参数修正的结果,Arrhenius模型的三个参数根据每个阶段温度的不同,在卡尔曼滤波的作用下实时修正,以此实现容量反馈修正。
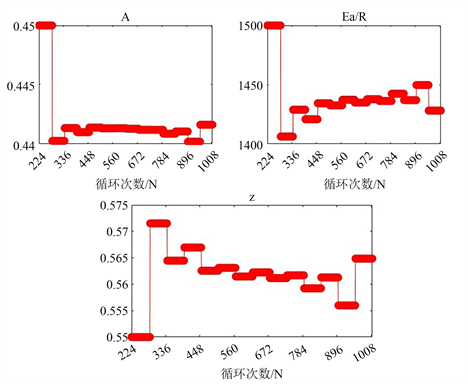
Figure 4. Model parameter update result graph
图4. 模型参数更新结果图
在Simulink建立的仿真模型上,使用NASA系统的某款三元里电池进行仿真模拟了该电池在动态工况下容量衰减的趋势。如图5所示,红色曲线代表电池容量实测结果,由于电池出厂时只提供一个出厂容量标签,而随着电池的老化,电池的实际容量也会发生衰减。而标准容量测试是在25℃的标准环境温度下进行先以标准充电电流恒流充电至电池端电压达到4.2 V充电截止电压,随后保持4.2 V电压改为恒压充电,充电电流逐渐降低,当充电电流达到设定的最低电流(一般为10 Ma)时,电池即完全充满;同样的环境温度下,以标准放电电流进行恒流放电,放电至2.5 V截止电压,电池此时完全放空。重复三次上述过程,设定取三次标准放电容量的平均值为电池的标准容量,以此作为实测值,通过实测值作为容量衰减过程中的容量标签来评估融合估计结果。绿色曲线代表容量在线辨识的结果,蓝色曲线代表双卡尔曼滤波的作用下容量融合估计的结果。可以看出相比于容量在线辨识的结果,融合估计的容量整体趋势更加接近实测值,且波动较小。
容量在线辨识与融合估计的误差结果如图6所示,根据容量估计结果与误差结果进行综合分析,可以看出,容量在线辨识的结果维持在4%以内,然而随着充放电循环次数的进行,容量在线辨识的稳定性难以得到保证。融合估计容量值在卡尔曼滤波的作用下,可以根据实际情况实时更新模型的参数,从而用新的参数对容量的结果进行实时修正。在老化循环的过程当中,融合估计容量的误差维持在3%以内,后期随着循环次数的增加,融合估计的误差可以维持在2%以内。容量融合估计的方法在改善容量估计精度的同时也提升了容量估计的鲁棒性。
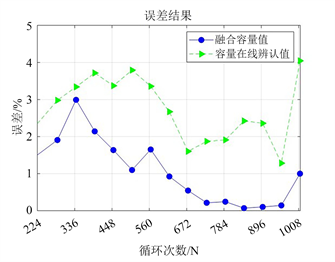
Figure 5. Fusion estimation capacity result graph
图5. 融合估计容量结果图
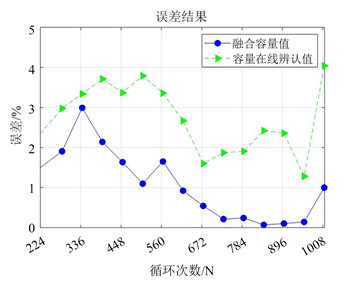
Figure 6. Fusion estimation error result chart
图6. 融合估计误差结果图
5. 结论
本文通过Simulink搭建仿真平台,首先通过SOC–电量增益法对电池的容量进行初步计算,随后针对实车场景多变导致的模型参数失配的问题,提出卡尔曼滤波来定期更新模型参数和阿伦尼乌斯容量衰减曲线。结果显示,本文所提出融合估计方法可以有效提高容量估计的精度和鲁棒性。容量估计误差维持在3%以内,适用于电动汽车BMS健康状态估计,在电动汽车领域有较好的应用前景。