基于SEA的上肢康复机器人按需辅助控制策略

Assist-as-Needed Control Strategy for Upper Limb Rehabilitation Robots Based on Serial Elastic Actuators (SEA)

摘要: 随着老龄化程度加深和因神经损伤等原因导致的上肢功能障碍者越来越多，对上肢康复机器人的研究也越来越深入，但目前针对上肢康复机器人临床使用中的安全性与稳定性的研究仍较少。本文为串联弹性驱动器(SEA)驱动的上肢康复机器人开发了一种“按需辅助”(AAN)控制方案。基于奇异摄动法，将SEA驱动的机器人模型分为慢时间尺度动力学和快时间尺度动力学，并分别设计导数控制项与按需辅助控制项，以实现误差跟踪和目标阻抗调制，实现满意的AAN特性和患者积极参与康复训练的目的。仿真结果表明，在速度域中建立基于模型的并发学习自适应阻抗控制器能够在保证跟踪精度的同时实现有效的按需辅助康复训练。

Abstract: With the deepening of aging and more and more people with upper limb dysfunction caused by nerve injury and other reasons, the research on upper limb rehabilitation robots is more and more in-depth, however, there are few studies on the safety and stability of the upper limb rehabilitation robot. In this paper, an assist-as-needed (AAN) control strategy is developed for an upper limb re-habilitation robot driven by series elastic actuators (SEA). Based on the singular perturbation method, the SEA-driven robot model is divided into slow-time-scale dynamics and fast-time-scale dynamics, to achieve error tracking and target impedance modulation, to achieve satisfactory AAN characteristics and patients actively participate in rehabilitation training purposes. The simulation results show that the model-based concurrent learning adaptive impedance controller in the veloc-ity domain can achieve effective AAN rehabilitation training while ensuring tracking accuracy.

1. 引言

通过上肢康复机器人辅助治疗已经成为一种行之有效的康复策略，可用于恢复和改善因老龄化或神经损伤等导致的上肢功能障碍 [1] 。与传统的康复治疗手段相比，上肢康复机器人不仅可以提供低成本、高质量的重复性训练，而且可以通过解析患者的运动意图和肌力恢复程度及时调整康复治疗策略，从而在以任务为导向的康复过程中极大地减轻医疗压力 [2] 。

尽管目前国内外已经有较为成熟的上肢康复机器人产品，如ArmMotus-M2 [3] 、ARMGUIDER [4] 、MIT-MANUS [5] 等，但是上肢康复机器人仍未在医院或康复中心得到广泛应用，这可能是以下两方面的原因：一是传统的上肢康复机器人通常采用刚性驱动器实现快速、准确和稳定的物理交互，这在机器人与人共享同一工作空间时是一个关键性的安全问题 [6] 。为此，研发人员开发了串联弹性驱动器(SEA)，通过给予机器人有限范围内的内在柔性，保证患者的安全 [7] 。

另一方面，康复机器人使用的控制策略对治疗效率有重要影响，而提高治疗效率的关键在于降低治疗成本与缩短治疗时间 [8] 。目前，康复策略中主要包括被动康复与主动康复策略，但根据诱导神经可塑性原理，相比于被动康复策略，通过充分利用患者剩余肌力的主动康复策略更有利于患者的运动功能重塑。因此，研究人员提出了根据患者自身生理状态与运动意图提供干预力的按需辅助(AAN)控制策略。

AAN控制器会根据用户的运动功能输入调整其干预措施，即机器人在患者能够完成康复任务时尽量减少干预，否则增加干预。用于运动功能输入的常见方法有：肌肉的肌电图信号 [9] 、基于模型的扰动观测器 [10] 、监测性能指标(通常是跟踪误差)以及末端力传感器信号等等。然而，上述的AAN控制方法大多都是在位置域中设计，这意味着它们的目标是最大限度地减少时变位置误差，不能为患者提供足够的时间自由度。

因此，本文以SEA驱动的上肢康复机器人为研究对象，通过机器人末端点的实时交互力来估计患者的运动意图，采用机器人工作空间中的速度矢量而不是位置矢量来编码所需的路径，保证康复训练的运动平滑度，同时监测速度域的跟踪误差，实时调节参考阻抗模型来实现AAN特性，提高康复训练的有效性与人机交互的安全性。

2. 上肢康复机器人动力学

假定所研究的上肢康复机器人有n个旋转关节，有SEA驱动的刚性连杆连接，如图1所示。根据机器人运动学模型，可以得到机器人末端相对于固定参考坐标系的姿态，用 $x\in R^l$ 表示，通过分析雅克比矩阵 $J\left(q_l\right)\in R^{lxn}$ ，可以得出机器人在操作空间中速度与关节角速度之间的关系，定义雅克比矩阵的右伪逆矩阵为 $J^{†}\left(q_l\right)\in R^{nxl}$ 。

假设1：在操作空间中，J(q_l)是有界的且具有满秩，因此逆矩阵 $J^{†}\left(q_l\right),J^{†}\left(q_l\right)$ 存在且有界。

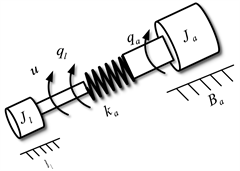
Figure 1. Diagram of the SEA’s structure

图1. SEA结构示意图

考虑一个由SEA驱动的上肢康复机器人，其动力学模型如下：

$\{\begin{array}{l}{J}_l{\ddot{q}}_l+B_l\left(q_l,{\stackrel{\dot{}}{q}}_l\right){\stackrel{\dot{}}{q}}_l+G\left(q_l\right)+F\left({\stackrel{\dot{}}{q}}_l\right)=K\left(q_a-q_l\right)+J^T{f}_{ext}\hfill \\ J_a{\ddot{q}}_a+K\left(q_a-q_l\right)=u\left(t\right)\hfill \end{array}$ (1)

其中 $q_l\left(t\right)\in R^n$ 和 $q_a\left(t\right)\in R^n$ 分别是电机角度向量和关节驱动器角度向量， ${\stackrel{\dot{}}{q}}_l,{\ddot{q}}_l\in R^n$ 分别表示关节角速度与角加速度， $J_l\in R^{nxn},B_l\in R^{nxn}$ 分别表示惯性与科里奥利矩阵， $G\left(q_l\right)\in R^n,F\left({\stackrel{\dot{}}{q}}_l\right)\in R^{nxn}$ 分别是重力矩与粘性摩擦。 $J_a\in R^{mxn}$ 和 $K\in R^{mxn}$ 分别是SEA的惯性矩阵和刚度矩阵， $f_{ext}\in R^l$ 是用户施加在末端的外力矢量，是有界的。

定义 $K\left(\theta -q\right)={\tau }_k$ ，则动力学模型(1)可以在假设1和笛卡尔空间变量下展开为：

$J_{lx}\left(x\right)\ddot{x}+B_{lx}\left(x,\stackrel{\dot{}}{x}\right)+G_x\left(x\right)+F_x\left(\stackrel{\dot{}}{x}\right)=J^{-T}{\tau }_k+f_{ext}$ (2)

其中 $J_{lx}\left(x\right),B_{lx}\left(x,\stackrel{\dot{}}{x}\right),G_x\left(x\right),F_x\left(\stackrel{\dot{}}{x}\right)$ 是 $J_l,B_l\left(q_l,{\stackrel{\dot{}}{q}}_l\right),G\left(q_l\right),F\left({\stackrel{\dot{}}{q}}_l\right)$ 通过雅克比矩阵J(q_l)在笛卡尔空间变换所得，只要雅克比矩阵不是奇异的，动力学(1)就具有以下性质：

性质1：矩阵J_lx，J_ax是正定对称的，且满足 $m_1{\Vert \lambda \Vert }^2\le {\lambda }^T\left(J_{lx}+J_{ax}\right)\lambda \le m_2{\Vert \lambda \Vert }^2,\forall \lambda \in R^n$ ，m₁，m₂是正常数。

性质2： ${\stackrel{\dot{}}{J}}_{lx}\left(q_l\right)-2B_{lx}\left(q_l,{\stackrel{\dot{}}{q}}_l\right)$ 是斜对称矩阵，且满足：

${\kappa }^T\left({\stackrel{\dot{}}{J}}_{lx}\left(q_l\right)-2B_{lx}\left(q_l,{\stackrel{\dot{}}{q}}_l\right)\right)\kappa =0,\forall \kappa \in R^n$ (3)

3. 速度场设计

为了实现SEA驱动机器人的末端点编码所需路径，首先需要创建一个所需的速度曲线，即为机器人操作空间中的每个点分配一个所需的速度，对于自由形态路径，可以通过确定当前位置与期望路径之间的位置矢量来实现。

设机器人工作空间中位置点为 $p\left(x,y,z\right)\in R^3$ ，假定期望运动路径为c，取Q为期望运动路径c到位置点 $p\left(x,y,z\right)$ 的最近点，该距离向量设为Q − p，可得该方向上归一化的法向向量 $\hat{n}\triangleq \left(Q-p\right)/\Vert Q-p\Vert$ ，定义 $\hat{t}$ 为归一化后的切向向量，如图2所示，利用工作空间中实际位置点与期望运动曲线间的切向向量与法向向量得到期望速度向量，计算公式如下：

$v_d\left(p\right)=\xi \left(\alpha \hat{t}+\Vert Q-p\Vert \hat{n}\right)$ (4)

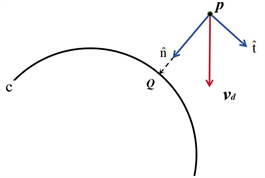
Figure 2. Tangential and normal vectors in the velocity field

图2. 速度场中切向向量与法向向量

其中 $\xi ,\alpha \in R^{+}$ 是正常数，调节 $\xi ,\alpha$ 之间的权重可以起到调节机器人运动速度与向期望运动曲线收敛速度的作用。根据式(4)，可以得到：

$v_d\left(p\right)=-2k\left(p\right)u\left(p\right)\left[\begin{array}{c}\left(x-x_c\right)\\ \left(y-y_c\right)\end{array}\right]+2c\left(p\right)\left[\begin{array}{c}-\left(y-y_c\right)\\ \left(x-x_c\right)\end{array}\right]$ (5)

其中 $u\left(p\right)={\left(x-x_c\right)}^2+{\left(y-y_c\right)}^2-r_0{}^2$ ， $k\left(p\right)=k_0/\left(\left|u\left(p\right)\right|\Vert \nabla u\left(p\right)\Vert +{\epsilon }_0\right)$ ，因此在文中，取初始位置向量 $p_0=\left[0,0.25,0\right]$ ，x_c = 0 m，y_c = 0 m，k₀ = 0.05 ms⁻¹，r₀ = 0.25 m，v₀ = 0.03 ms⁻¹，ε₀ = 0.01 m²和c₀ = 100 mm²。图3为文中所描述的笛卡尔坐标下的速度场。

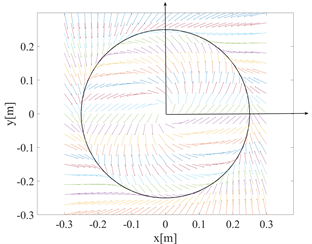
Figure 3. Velocity field in Cartesian coordinates

图3. 笛卡尔坐标下速度场

4. 控制器设计

基于奇异摄动法 [7] ，动力学(1)中弹簧刚度矩阵可以表示为 $K=K_0/{\epsilon }^2$ ，其中 $\epsilon \in R^{+}$ 是一个无限小的正参数， $K_0\in R^{nxn}$ 是正定对角矩阵，由此动力学(1)可以表示为：

$\{\begin{array}{l}{J}_l\left(q_l\right){\ddot{q}}_l+B_l\left(q_l,{\stackrel{\dot{}}{q}}_l\right){\stackrel{\dot{}}{q}}_l+G\left(q_l\right)+F\left({\stackrel{\dot{}}{q}}_l\right)={\tau }_k+J^T{f}_{\text{ext}}\hfill \\ {\epsilon }^2{J}_a{\ddot{\tau }}_k+K_0{\tau }_k=K_0\left(u-J_a{\ddot{q}}_l\right)\hfill \end{array}$ (6)

定义位置跟踪误差 $e\left(t\right)=q_d\left(t\right)-q_l\left(t\right)$ ，其中q_d(t)是期望电机角度位置，定义 $\ddot{e}={\ddot{q}}_d-{\ddot{q}}_l$ ，式(6)可展开表示为如下标准奇异摄动形式：

$\{\begin{array}{ll}\stackrel{\dot{}}{a}=g\left(a,b,t\right),\hfill & a\left(0\right)=a_0\hfill \\ \epsilon \stackrel{\dot{}}{b}=h\left(a,b,t\right),\hfill & b\left(0\right)=b_0\hfill \end{array}$ (7)

其中 $a=\mathrm{col}\left(e,\stackrel{\dot{}}{e}\right),b=\mathrm{col}\left({\tau }_k,\epsilon {\tau }_k\right),a_0,b_0\in R^{2n}$ ，定义 $W\left(q_l,{\stackrel{\dot{}}{q}}_l\right)=B_l\left(q_l,{\stackrel{\dot{}}{q}}_l\right)+G\left(q_l\right)+F\left({\stackrel{\dot{}}{q}}_l\right)$ ，因此可得 $g,h\in R^{2n}$ 为：

$g\left(a,b,t\right)=\left[\begin{array}{c}\stackrel{\dot{}}{e}\\ -J_l^{-1}\left(q_l\right)\left({\tau }_k-W\left(q_l,{\stackrel{\dot{}}{q}}_l\right)\right)+{\ddot{q}}_{ld}\end{array}\right]$ (8)

$h\left(a,b,t\right)=\left[\begin{array}{c}\epsilon {\stackrel{\dot{}}{\tau }}_k\\ K_0\left[J^{-1}\left(u-{\tau }_k\right)+J_l^{-1}\left(q_l\right)\left(W\left(q_l,{\stackrel{\dot{}}{q}}_l\right)-{\tau }_k\right)\right]\end{array}\right]$ (9)

由于式(6)在ε = 0处有唯一的孤立根，即 ${\tau }^{*}=h\left(a,t\right)=u_s-J_a{\ddot{q}}_l$ ，那么通过式(6)和τ^* = τ，可以建立一个式(7)在ε = 0处的简化系统，即一个准稳态系统模型：

$\left(J_l\left(q_l\right)+J_a\right)\left({\ddot{q}}_{ld}-\ddot{e}\right)+W\left(q_l,{\stackrel{\dot{}}{q}}_l\right)=u_s$ (10)

定义一个新的时间变量 $t_{\epsilon }=t/\epsilon$ ，和一个新的状态变量 $\eta =\tau -h\left(a,t\right)$ ，当ε = 0时，因为变量a和t分别被“冻结”在a₀与0处， $h\left(a,t\right)$ 在快时间尺度t_ε下是常数。然后，将 $\tau =\eta +h\left(a,t\right)$ 与代入式(7)，可以得到如下快时间尺度的表达式：

${\eta }^{″}+K_0\left(J_l^{-1}\left(q_l\right)+J_a^{-1}\right)\left(\eta +h\left(a,t\right)\right)=K_0{J}_a^{-1}u+K_0{J}_l^{-1}\left(q_l\right)W\left(q_l,{\stackrel{\dot{}}{q}}_l\right)$ (11)

其中 ${\eta }^{\prime }:=\text{d}\eta /\text{d}{t}_{\epsilon }$ ，基于上述推导，有关式(7)的边界层系统为：

${\eta }^{″}+K_0\left(J_l^{-1}\left(q_l\right)+J_a^{-1}\right)\eta =K_0{J}_a^{-1}{u}_f$ (12)

根据准稳态系统模型(10)和边界层系统模型(12)，可以将SEA驱动机器人动力学模型(6)分解为一个刚性机器人模型与SEA模型，可以得到以下控制器， $u_s\in R^n,u_f\in R^n$ 分别表示慢时间尺度与快时间尺度下的控制器：

$u=u_s\left(a,t\right)+u_f\left(\stackrel{\dot{}}{\eta },\epsilon \right)$ (13)

将快时间尺度控制器u_f设计为：

$u_f=-K_{\theta }\left({\stackrel{\dot{}}{q}}_a-{\stackrel{\dot{}}{q}}_l\right)$ (14)

其中 $K_{\theta }=K_d/\epsilon \in R^{nxn}$ ，K_d是正定对角矩阵。

针对慢时间尺度控制器u_s的设计，先假设上肢康复机器人末端存在力传感器，可以记录用户所施加的交互力信息f_ext。因此，根据速度场中所定义的期望参考速度v_d，设计如下阻抗模型：

$J_i\left(\ddot{x}-{\stackrel{\dot{}}{v}}_d\right)+D_i\left(\stackrel{\dot{}}{x}-v_d\right)=f_{ext}$ (15)

其中 $J_i,D_i\in R^{lxl}$ 是正对角矩阵，由于实际中精准的系统动力学模型不可知，为了避免使用加速度信息而引入高频噪音等干扰，建立如下的中间阻抗模型，定义一个中间参考速度 $v_i\in R^l$ 为 $M_i{\stackrel{\dot{}}{v}}_i+D_i{v}_i=M_i{\stackrel{\dot{}}{v}}_d+D_i{v}_d+f_{ext}$ 的输出：

$J_i\left({\stackrel{\dot{}}{v}}_i-{\stackrel{\dot{}}{v}}_d\right)+D_i\left(v_i-v_d\right)=f_{ext}$ (16)

因此可以得出，当 $\stackrel{\dot{}}{x}$ 收敛至v_i时，中间目标阻抗(16)收敛到(15)，并满足期望阻抗，设计误差向量 $e_r\in R^l$ 为：

$e_r=\stackrel{\dot{}}{x}-v_i$ (17)

根据笛卡尔空间变换原理，式(1)中的SEA驱动机器人动力学模型可以写为：

$\left(J_{lx}\left(x\right)+J_{ax}\right){\stackrel{\dot{}}{e}}_r=-B_x\left(x,\stackrel{\dot{}}{x}\right)e_r+N+J^{-T}{u}_s+f_{ext}$ (18)

其中在R^l中定义 $N\left(x,\stackrel{\dot{}}{x},v_i,{\stackrel{\dot{}}{v}}_i\right)$ 为 $N=-B_x\left(x.\right)-G_x\left(x\right)-F_x\left(\stackrel{\dot{}}{x}\right)-J_{alx}{v}_i$ 。通过基于模型的并发学习自适应控制策略对N进行估计，使得包含了未知动态项的N可以在一个紧凑集Ω_N上表示为：

$\hat{N}\left(x,\stackrel{\dot{}}{x},v_i,{\stackrel{\dot{}}{v}}_i\right)=Y\left(x,\stackrel{\dot{}}{x},v_i,{\stackrel{\dot{}}{v}}_i\right)\hat{\sigma }$ (19)

通过对未知函数N的估计，定义正定对角矩阵K_r，慢时间尺度控制器设计为：

$u_s=-J^T\left(K_r{e}_r+\hat{N}\right)-J^T{f}_{\text{ext}}$ (20)

5. 仿真验证与分析

利用MATLAB对以上控制率进行了模拟仿真，选择一个二连杆SEA驱动的上肢康复机器人作为控制对象，通过控制器(13)实现对式(1)的按需辅助控制分析。上肢康复机器人矩阵参数如下：

$\{\begin{array}{l}{J}_l\left(q_l\right)={\left[J_{ij}\right]}_{2\times 2},j=1,2,\hfill \\ B_l\left(q_l,{\stackrel{\dot{}}{q}}_l\right)=\left[\begin{array}{cc}v{\stackrel{\dot{}}{q}}_{l2}& v\left({\stackrel{\dot{}}{q}}_{l1}+{\stackrel{\dot{}}{q}}_{l2}\right)\\ -v{\stackrel{\dot{}}{q}}_{l1}& 0\end{array}\right],\hfill \\ J_a=0.14I_{2\times 2},K=diag\left\{400,400\right\}\hfill \end{array}$ (21)

其中m₁ = 1 kg，m₂ = 1 kg，l₁ = 0.25 m，l₂ = 0.25 m，I₁ = 0.25 kg∙m，I₂ = 0.1 kg∙m，为了实现AAN特性，有必要监测系统性能以改变阻抗参数，可变阻抗的动态调制由以下函数所完成： $D_i=\mathrm{diag}\left\{{\lambda }_1,{\lambda }_2\right\}$ ，Ji = diag $\left\{0.66,0.66\right\}$ 其中 ${\lambda }_j=100\tanh \left(400\varpi \left(\left|e_j\right|,\gamma \right)\right)+D_0,j=1,2$ 。

仿真结构如图4~7所示：

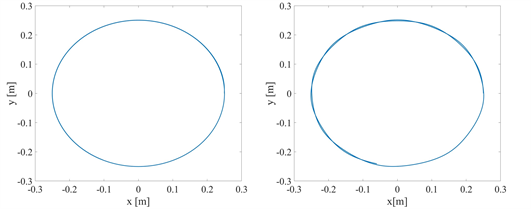
Figure 4. Trajectory of the robot end-effector, without f_ext, with f_ext

图4. 机器人末端执行器的轨迹(无外力、有外力)

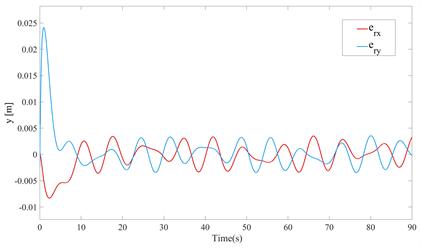
Figure 5. Error of the robot end-effector

图5. 机器人末端执行器的误差

Figure 6. Control input of the robot

图6. 机器人控制输入

Figure 7. Modulated D_i

图7. 调制的D_i

经过仿真分析，图4表示在有无外力的情况下机器人沿着X轴、Y轴两个方向上对期望路径的轨迹跟踪情况，可以看出实际轨迹几乎贴合所设计的期望路径。图5表示为模拟患者主动康复训练下，机器人在X轴、Y轴的运动轨迹误差，由于机器人的初始速度为零，导致开始时机器人位置误差较大，但随着康复训练的进行，其运动轨迹跟踪误差逐渐趋于稳定，证明了该策略可以保证机器人进行有效的轨迹跟踪，提供平滑稳定的康复训练。控制器的控制输入如图6所示。在初始阶段，由于运动状态出现了突然变化导致控制扭矩相对较大，此后，控制扭矩逐步平稳。

因控制器式(13)本身不单独提供AAN特性，而是通过可变阻抗模型(16)，为此，通过调制D_i，使得总阻抗在误差 $e_r=\stackrel{\dot{}}{x}-v_i$ 小时减小，增大时增大。那么，假设当前施加的f_ext可以使得 $\stackrel{\dot{}}{x}\to v_d$ ，总阻抗将降低，机器人在跟随期望速度时将会提供一定的支持辅助。在这种情况下，即v_i将收敛于v_d，x在v_d附近，在用户输入过大或在错误方向上施加的情况下，跟踪误差e_r将增加，这导致机器人呈现高的期望阻抗，以将肢体推向期望的方向 [8] 。图7为根据外界输入力的大小所调制的机器人阻抗参数，可以看出，在运动过程中，当患者施加过大的外力f_ext时，存在一个正常数 $\gamma \in R^{+}$ ，使得 $\left|e_r\right|\le \gamma$ 时，阻抗参数被设置为初始值 $D_0=0.44$ ，当 $\left|e_r\right|\ge \gamma$ 时，阻抗参数则逐步增大到所设置的极值 $D_{\max }=0.64$ 。

6. 结语

本文研究了串联弹性驱动器驱动的上肢康复机器人的按需辅助控制问题，为了获取康复训练中足够的时间自由度，最大限度地提高受试者在康复训练中的积极性。通过在速度域中定义运动问题，同时考虑速度容许范围。基于这一核心思想，我们设计了一种用力传感器测量用户输入，考虑机器人可变目标阻抗来实现控制目标的控制方案。通过在SEA驱动的平面上肢二自由度上肢康复机器人上进行的模拟仿真实验，对控制器进行了评价。结果表明，当受试者参与康复训练中，控制器可以对期望路径进行准确跟踪，且当受试者输入力过大或在错误方向上施加的情况下，机器人也可呈现出高阻抗的特性，以辅助受试者重新回归至期望位置。在保证康复训练中受试者安全与舒适的前提下，能够产生足够的自由度用于受试者的主动参与，提高受试者的训练积极性。未来的工作将侧重于进一步实验验证，并实现患者在任意路径下实现高效率、高质量的康复训练。

致谢

作者衷心感谢国家自然科学基金项目(62073156、62103280)的资助。

参考文献