摘要:
贝叶斯模型为解释类别归纳推理的实验现象提供了一个统一的可计算框架。在该框架下,用不同的类别结构和随机过程表示不同的先验知识,并基于贝叶斯公式预测不同场景下的归纳力度。与其它模型相比,贝叶斯模型有较强的预测力度和更广的应用范围。文章总结了该模型的发展历史及现状,并首次系统阐述了其建模过程。未来研究可结合功能磁共振实验和计算语言学等方法,进一步拓展该模型的推理能力,提高其实际可用性。
Abstract:
The Bayesian model (BM) of category-based induction provides a unified computable framework for explaining the experimental phenomena (including the premise-conclusion similarity effect, the premise diversity effect, the premise monotonic effect and the premise-conclusion asymmetric effect, etc.) in category-based induction. Within this framework, the inductive reasoning in different contexts (such as induction about the generic biological properties or the causally transmitted properties) requires the constraint of different kinds of prior knowledge. Different kinds of prior knowledge can be represented by different kinds of category structures (i.e., the relationship between categories) and the corresponding stochastic process (i.e., the distribution of features/ properties in the category structure). Thus, BM can get the prior probability distributions for the Bayesian inference engine, and finally, the strength of an inductive argument can be calculated. As compared to the similarity coverage model (SCM) and feature-based inductive model (FBIM), BM can reflect the interaction of categories and properties, and has a clear mathematical basis, and also shows a better ability of prediction. This paper firstly reviews the research history and state of the art of the BM, and summarizes the process of computational cognitive modeling using BM. Secondly, BM is compared with the other models, and then the advantages and disadvantages of the BM are commented in details. Finally, some potential research directions are proposed: 1) further improving the ability of BM to deal with the common sense knowledge (e.g., the predatory behavior of animal), which may help to expand its application scope; 2) further increasing the power of BM to handle multiple objects and features/properties (if we learn that the animal A has the property X, what’s the possibility of the animal B having the property Y?); 3) that in combination with other methodologies (e.g., functional magnetic resonance imaging (fMRI) and computational linguistics, such as corpora), BM may improve its practical availability and reasoning abilities.
1. 引言
归纳推理是人类智力的核心成分之一,也是日常生活的一部分。通过归纳推理,人们可根据部分推测整体,根据已知推测未知。类别归纳推理是一类重要的归纳推理,即根据给定的一个或多个前提来推测结论成立的可能性,成立的可能性被称为归纳力度,如:已知牛有T4,判断马有T4的可能性,可简记为牛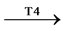 马。其中牛为前提类别,马为结论类别,T4为类别的特征,马有T4的可能性为该论断的归纳力度。根据结论类别的不同,论断分为三种:结论类别与前提类别在同一水平的为特殊论断,如牛
马。其中牛为前提类别,马为结论类别,T4为类别的特征,马有T4的可能性为该论断的归纳力度。根据结论类别的不同,论断分为三种:结论类别与前提类别在同一水平的为特殊论断,如牛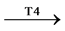 马;结论类别为包含所有前提类别的上位水平类别的为泛化论断,如牛、马
马;结论类别为包含所有前提类别的上位水平类别的为泛化论断,如牛、马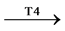 家畜;结论类别为只包含部分前提类别的上位水平类别为混合论断,如麻雀、牛
家畜;结论类别为只包含部分前提类别的上位水平类别为混合论断,如麻雀、牛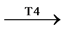 鸟。
鸟。
在类别归纳推理的研究中,已发现许多稳定的心理学效应,可分为类别效应、属性效应和类别-属性交互效应三类(陈安涛,李红,2003)。类别效应包括相似性效应、多样性效应等(Osherson, Smith, Wilkie, Lopze & Shafir, 1990; Sloman, 1993)。属性效应包括属性稳定性效应(陈安涛,李红,2003)、属性中心性效应(张婷婷等,2007)。类别–属性交互效应指在类别归纳推理中,对相同的类别,属性/特征的改变(如解剖学属性变为捕食行为属性)可能会显著地影响归纳力度的判断(陈安涛,李红,2003)。
认知心理学家提出许多认知模型解释这些心理效应,包括相似性覆盖模型(Similarity-Coverage Model, SCM)(Osherson et al., 1990)、基于特征的归纳模型(Feature-Based Inductive Model, FBIM)(Sloman, 1993)、假设检验模型(McDonald, Samuels & Rispoil, 1996)、贝叶斯模型(Bayesian Model, BM)(Heit, 1998; Tenenbaum, Kemp & Shafto, 2007)、相关理论模型(Medin, Coley, Storms & Hayes, 2003)、关联相似性模型(王墨耘,莫雷,2006)及抽样理论模型(王墨耘,2008)。其中,SCM、FBIM和BM为可计算模型。SCM基于相似性和覆盖的线性组合计算论断归纳力度,其中,相似性指前提类别和结论类别间的相似度;覆盖指前提类别和包含前提和结论类别的最低上位水平类别的相似度。FBIM基于前提类别和结论类别间特征重叠程度计算论断归纳力度。这两种模型都强调相似性的作用,可较好解释和预测对一般生物属性(空白属性)的类别归纳推理。但这两种模型均有一定的局限性:首先,它们都不能准确预测因果关系属性的类别归纳推理,也不能解释类别–属性交互效应;其次,两者的数学基础均不严密(Tenenbaum et al., 2007):SCM预测的准确性依赖于模型的数学形式;FBIM用特殊的数学方法测量特征重叠度,但很难评估其正确性。SCM和FBIM的不同在于FBIM预测准确性较低,但却可预测一些SCM不能解释的定性现象如前提–结论包含相似性效应等(Sloman, 1993)。
与SCM和FBIM不同,类别归纳推理的贝叶斯模型(Tenenbaum et al., 2007)结合了结构化知识表示和贝叶斯推理,有明确的数学基础,用不同种类先验知识对多种场景下的类别归纳推理进行预测,增强了解释效力,为解释类别归纳推理的心理效应提供了一个统一的框架。
2. 类别归纳推理的贝叶斯模型研究历史
Heit(1998)最早将贝叶斯模型引入类别归纳推理研究中。基于给定的先验概率,其模型可解释一些归纳推理的心理效应如相似性效应、典型性效应等。尹静和王墨耘(2009)对Heit的贝叶斯模型进行了实验检验,验证其在一定程度上可准确预测论断归纳力度。然而,Heit没有提出产生先验概率的方法,只是假设先验概率可从记忆中提取。之后,Yafen Lo等(2002)用贝叶斯公式证明了前提概率原则,即论断前提同时成立概率越低,论断的归纳力度越强。前提概率原则可很好地解释多样性效应,但无法解释其它心理效应。
与Heit(1998)贝叶斯模型不同,Tenenbaum等给出了具体的先验概率计算方法。Tenenbaum等把先验知识形式化为表示类别间关系的类别结构和表示属性在类别间分布的随机过程,并给出两个子模型:对一般生物属性推理的树状模型,该模型体现了相似类别更可能有相同的一般生物属性这一先验知识(Sanjana & Tenenbaum, 2002; Kemp & Tenenbaum, 2003; Tenenbaum et al., 2007; Griffiths et al., 2008);对疾病推理的因果传递模型,该模型体现了疾病更可能由被捕食者传递给捕食者这一先验知识(Shafto et al., 2005; Tenenbaum et al., 2006; Tenenbaum et al., 2007)。
Tenenbaum贝叶斯模型可对不同场景的类别归纳推理进行预测和解释,体现了类别–属性交互效应。例如,Shafto等(2008)对基因和疾病推理的研究表明不同属性的类别归纳推理需要不同种类的先验知识进行约束,体现了属性改变对类别归纳推理的影响。
Tenenbaum贝叶斯模型先验概率的计算依赖于表征知识的类别结构和随机过程。结构算法只能生成指定的结构,不能用于类别结构未知的场景。Kemp和Tenenbaum(2008)提出一种结构学习算法,该方法可学习不同形式的结构并选出最适合给定数据的结构。在此基础上,该模型增加了两个子模型:空间子模型和阈值子模型,扩展了其推理能力(Kemp & Tenenbaum, 2009)。
3. Tenenbaum贝叶斯模型
Tenenbaum贝叶斯模型分为两部分:1) 先验知识表征,用类别结构和随机过程表征先验知识,为所有假设(所有类别状态为一个假设,对应一个特征向量)分配先验概率。2) 贝叶斯推理机,基于贝叶斯公式进行归纳推理,且独立于推理场景。该模型的建模过程见图1。
3.1. 先验概率计算方法
先验概率的产生是贝叶斯模型的一个重要问题。简单指定所有假设有相同的先验概率,无任何偏置,不能产生有效的归纳。同时,先验概率是知识抽象的产物,所以不能随机枚举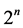 个数字。不同属性的归纳推理需要不同种类的知识约束,以产生合理的先验概率分布(Tenenbaum et al., 2007)。
个数字。不同属性的归纳推理需要不同种类的知识约束,以产生合理的先验概率分布(Tenenbaum et al., 2007)。
Tenenbaum贝叶斯模型基于两种知识产生先验概率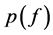 :所有类别间的关系和特征在类别间的分布。这两种知识形式化为类别结构S和建立在S上的随机过程T(Tenenbaum et al., 2007; Kemp & Tenenbaum, 2009)。结合不同类别结构和随机过程,可表示不同种类的知识,进而预测不同场景下的类别归纳推理。
:所有类别间的关系和特征在类别间的分布。这两种知识形式化为类别结构S和建立在S上的随机过程T(Tenenbaum et al., 2007; Kemp & Tenenbaum, 2009)。结合不同类别结构和随机过程,可表示不同种类的知识,进而预测不同场景下的类别归纳推理。
类别结构常用图状结构表示,不同的图状结构表示不同的类别关系,见表1。其中,树状结构和低维空间结构可通过结构学习方法获得。
随机过程表示属性在类别结构上的分布,不同的随机过程表示不同的分布方法。定义在不同结构上的随机过程产生的先验概率表征不同的知识,常用随机过程见表2。
相应地,目前Tenenbaum贝叶斯模型有树状子模型、因果传递子模型、空间子模型和阈值子模型,
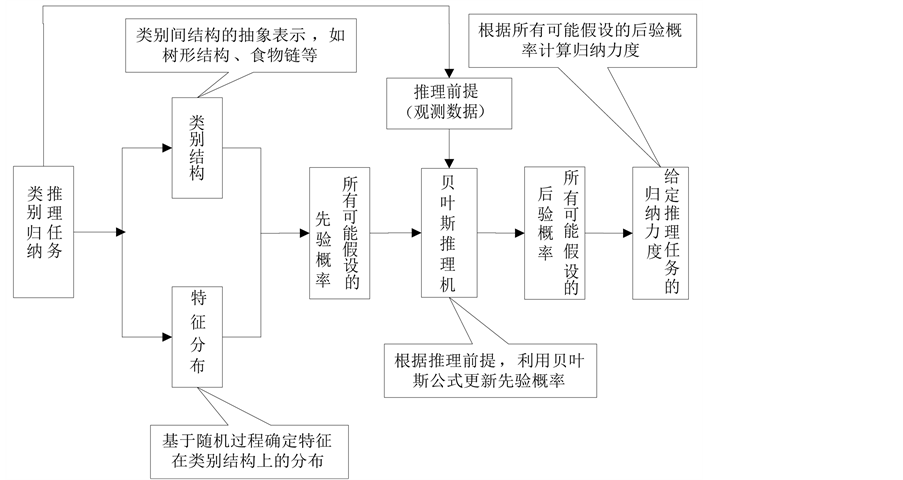
Figure 1. Process of modeling
图1. 建模过程

Table 1. The commonly used category structure
表1. 常用类别结构
分别用不同的结构和随机过程生成先验概率,表征不同的知识,用于不同场景的类别归纳推理。
下面以树状子模型为例说明如何生成先验概率。假设已知类别间相似性,对相似性进行聚类,可获得树状结构如图2(a)。然后,用突变过程生成先验概率。假定树的根节点有一个特征值(0或1)并沿分支传播。传播时每个分支节点有一个突变率,且分支节点是否发生突变独立。分支分裂时若未突变,则下级节点继承其上一级节点的特征值。例如,图2(a)中根节点特征值为0,但图2(b)中标记的分支发生突变,其下级节点特征值变为1(图中黑色的点),称图2(b)为突变史。
突变过程用参数λ描述,两节点有不同特征值的概率为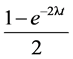 (t为分支长度)并假设根节点特征值
(t为分支长度)并假设根节点特征值
是0或1的概率相同且突变方向(0到1,1到0)等可能,然后计算每个突变史的概率。大量仿真后,计算与特征向量一致突变史的频率,作为该特征向量的先验概率(Tenenbaum et al., 2007)。这样生成的先验概率有些定量特性:首先,先验分布非零;其次,先验分布变化平滑:相邻类别更可能有相同特征。
3.2. 贝叶斯推理机
在Tenenbaum贝叶斯模型中,不同推理场景用不同的方法分配先验概率,但都用相同的贝叶斯推理机进行推理。假设领域内有n个类别,特征为Q。类别是否有Q由该类别的特征值表示,若类别有Q则特征值为1,否则为0。n个特征值组成一个表示n个类别是否有Q的n维向量f,其个数是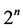 。设观测
。设观测

Table 2. The commonly used stochastic process
表2. 常用随机过程
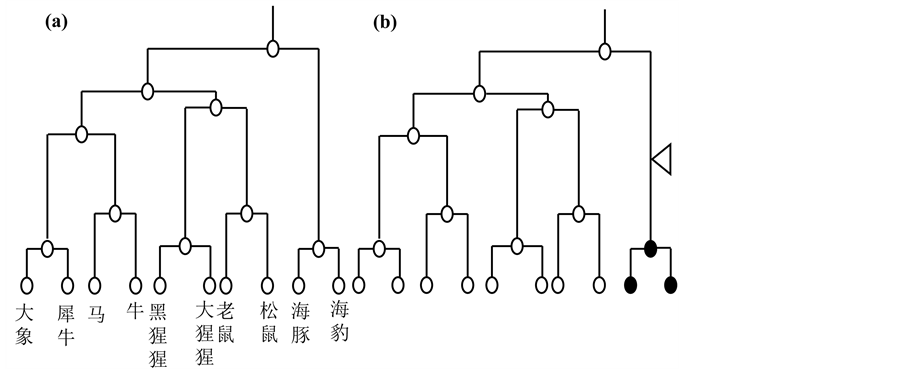
Figure 2. (a) A classification tree represents the taxonomic relationship among mammal categories; (b) An example of mutation histories. The triangle represents the occurring of a branch mutation, which induces the feature value change of the corresponding lower nodes. Source: Tenenbaum et al., 2007.
图2. (a) 表示类别间分类关系的分类树;(b) 为突变史,三角形表示该分支发生突变,下级节点的特征值发生改变。资料来源:Tenenbaum et al., 2007.
到子集X的特征向量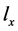 ,
,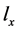 的特征值表示X中的类别是否有Q。据贝叶斯公式可计算出已知
的特征值表示X中的类别是否有Q。据贝叶斯公式可计算出已知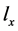 成立,f成立的后验概率
成立,f成立的后验概率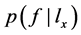 :
:
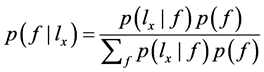 (1)
(1)
其中分母是对所有可能f求和,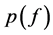 为先验概率,是已知量,
为先验概率,是已知量,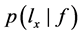 表示已知f成立,
表示已知f成立,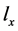 成立的概率。
成立的概率。
公式(1)的计算依赖于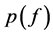 和
和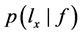 。
。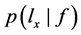 依赖于形成
依赖于形成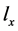 的过程,即X和
的过程,即X和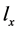 的生成过程(Kemp & Tenenbaum, 2009)。为简化计算,从f中取出X的特征值组成
的生成过程(Kemp & Tenenbaum, 2009)。为简化计算,从f中取出X的特征值组成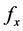 ,若
,若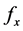 与
与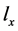 相等则称f和
相等则称f和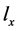 一致,
一致,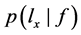 ∝1,否则
∝1,否则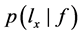 ∝0。
∝0。
据对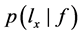 的假设,公式(1)化为:
的假设,公式(1)化为:
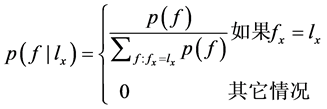 (2)
(2)
公式(2)中分母是对所有属于集合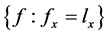 的特征向量求和,即所有与
的特征向量求和,即所有与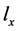 一致f的先验概率求和。而与
一致f的先验概率求和。而与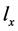 不一致特征向量的后验概率为0,进而计算出所有特征向量的后验概率。
不一致特征向量的后验概率为0,进而计算出所有特征向量的后验概率。
根据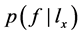 ,可计算
,可计算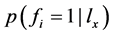 ,即已知
,即已知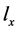 成立,类别i有Q的后验概率:
成立,类别i有Q的后验概率:
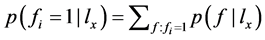 (3)
(3)
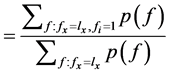 (4)
(4)
由公式(4)知,知道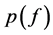 就可计算出每个类别有Q的后验概率。公式(4)还表明
就可计算出每个类别有Q的后验概率。公式(4)还表明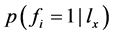 等于与
等于与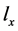 一致且含
一致且含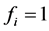 的特征向量占所有与
的特征向量占所有与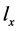 一致特征向量的比例,向量的权重由先验概率决定。
一致特征向量的比例,向量的权重由先验概率决定。
对其它类型论断(如泛化论断、混合论断)的推理也采用相似的方法。如,已知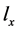 成立,可计算集合Y(如家畜或鸟)中类别有Q的后验概率
成立,可计算集合Y(如家畜或鸟)中类别有Q的后验概率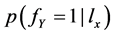 :
:
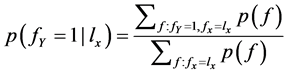 (5)
(5)
由上可知,获得先验概率后,用贝叶斯公式可计算出任何论断的归纳力度。
4. Tenenbaum贝叶斯模型的评价
Tenenbaum贝叶斯模型为理解类别归纳推理的心理现象提供了一个统一的框架,其优点在于:首先,该模型由多个子模型构成,用于不同的推理场景,具有很好的灵活性和较强的预测力度。其次,该模型对先验知识很敏感,不同的先验知识必须用不同的结构和随机过程表示,体现了类别–属性交互效应。再次,该模型用贝叶斯公式进行推理,有明确的数学基础。另外,与FBIM和SCM相比,该模型有更广的应用范围,见表3。
Tenenbaum贝叶斯模型仍存在不足:首先,该模型虽能定量的预测归纳力度,且其结果也表现出很多心理效应如相似性效应、多样性效应等,但却不能直观、定性地解释这些效应。其次,该模型可很好的模拟人类归纳推理行为,但不能模拟归纳推理过程,未揭示其本质。再次,该模型的计算仍需评分(如相似性),模型输出有一定的主观性。另外,贝叶斯推理计算复杂,不能很好预测归类不确定场境下的归纳推理行为(王墨耘,莫雷,2005)。

Table 3. The application range of SCM, FBIM and Bayesian model
表3. SCM、FBIM和贝叶斯模型应用范围
5. 研究展望
针对上述不足,未来需要从以下几方面进行深入研究:
首先,该模型目前可用于一般生物特征等四种特征的类别归纳推理,但尚不适用于行为特征等(如动物捕食行为)的归纳推理。研究如何使用该模型对这些特征进行归纳推理,提高其归纳推理能力,是未来研究的一个重要方向。
其次,类别归纳推理的研究多局限于单一特征在多个类别中存在情况的研究,而对多类别和多特征交叉归纳推理问题(如:已知A有基因X,判断B有酶Y的可能性)研究较少(Kemp et al., 2012),未来需要进一步深入研究。
另外,该模型常需要计算类别间的相似性。目前,相似性主要通过评分获得,具有一定的主观性,且难以获取大量数据,限制了其实际应用。基于语料库的统计分析获取相似性(Sakamoto et al., 2007)或基于功能磁共振实验数据计算相似性(Weber et al., 2009)可能有助于获得大量、相对客观的数据,未来需对这些方法进行深入的实验研究。
基金项目
国家自然科学基金青年基金项目(61105118),北京市科技新星项目(Z12111000250000, Z131107000413120),认知神经科学与学习国家重点实验室开放课题重点项目(CNLZD1302)。

NOTES
*通讯作者。