1. 引言
悬浮隧道是一个穿越水域的新的交通形式,目前世界上还有一个实际建成的悬浮隧道工程项目。它可以通过结构的自重、浮力、锚固系统的共同作用来在水中保持平衡和稳定。由于悬浮隧道处于相对比较复杂的水环境中,它受到波浪、水流等因素的影响,悬浮隧道的涡激振动已经成为广大科研工作者进行理论、试验、数值研究的课题,并且悬浮隧道的动力响应值得进行深入地研究。
由于悬浮隧道广泛的应用前景,广大的科研工作者从不同方面、不同视角着眼于它的研究。F. Brancaleoni等[1] 集中于对悬浮隧道在所处环境的响应问题研究;Remseth等[2] 则研究了悬浮隧道流固相互作用及其动力响应;E. de Langre等[3] 着眼于耦合模态颤振引起的频率锁定问题;R. Violette and E. de Langre[4] 研究出一种针对涡激振动和波浪的线性稳定的方法;Wei Lu等[5] 致力于波浪条件下悬浮隧道锚索的松弛现象和拉断力的研究;M.J. Pang and J.J. Wei[6] 则聚焦于升力和拖曳力系数的研究;S. Tariverdilo[7] 等主要针对悬浮隧道在移动荷载作用下的振动研究;项贻强等[8] 对悬浮隧道管体和锚索的耦合模型的涡激振动动力响应方面的研究作出了贡献。
在过去数年里,众多科研工作者已经对悬浮隧道管体、锚索、管体和锚索耦合模型的动力响应做了研究。很少有将将悬浮隧道简化成一个两端支座处带有弹簧和阻尼的弹性支撑梁来进行研究。在这章中,主要的研究工作集中于稳定流中涡激振动作用下的弹性支撑的悬浮隧道的动力响应。在这个过程中,悬浮隧道被简化成一个简支弹性梁和一个具有弹簧和阻尼支撑的刚性梁的叠加。
在前人研究的基础上,在本章中首先建立悬浮隧道在均匀流中的涡激振动作用下的动力平衡方程,通过采用Galerkin法和模态叠加法获得方程的解析解。然后利用Matlab软件对悬浮隧道跨中的位移进行模拟和分析,并得出理论和工程实践有意义的成果。
2. 均匀流中涡激振动作用下悬浮隧道的模型
2.1. 悬浮隧道的物理模型
对于原始未经任何简化的悬浮隧道模型来说,其结构极其的复杂,如图1、图2所示。由于悬浮隧道的张力腿位于悬浮隧道的跨中,使得对悬浮隧道进行动力响应研究显得很复杂。为了便于从理论上对悬浮隧道进行研究,可以将张力腿简化成悬浮隧道两端支座处的弹簧。简化完的悬浮隧道的物理模型如图3、图4所示。
如果使用一个精确的数学方法来求解悬浮隧道的动力平衡方程的话,考虑多阶模态会极其复杂,是
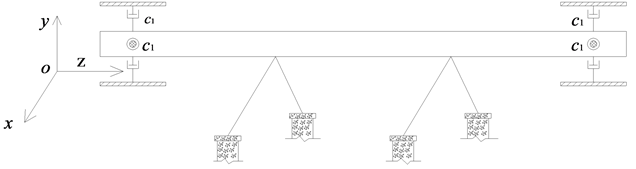
Figure 1. Schematic diagram of SFT model
图1. 悬浮隧道模型示意图
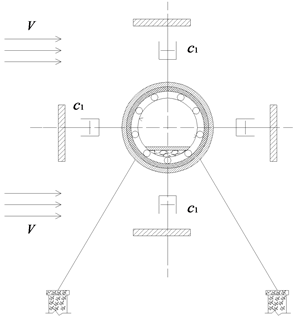
Figure 2. Schematic cross section of SFT on the tension leg
图2. 悬浮隧道张力腿处横截面示意图
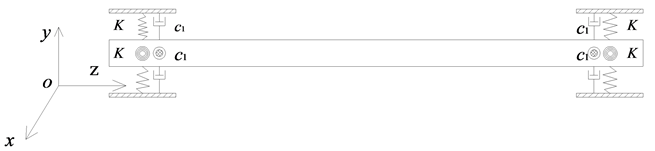
Figure 3. Schematic diagram of SFT simplified physical model
图3. 简化的悬浮隧道物理模型示意图

Figure 4. Schematic diagram of SFT simplified physical model on the tension leg
图4. 简化的悬浮隧道物理模型张力腿处横截面示意图
的很难获得一个近似的解析解。为此我们采用的悬浮隧道计算模型如图2~4所示,将悬浮隧道简化成一个两端由相同支座支撑的梁。悬浮隧道被简化成由一个弹性梁和一个刚性梁叠加。关于悬浮隧道在涡激振动作用下的一系列相应假设如下[9] :
1) 悬浮隧道跨中的张力腿被简化成两端支座处的弹簧;
2) 被简化的两端支座处的弹簧的竖向刚度为K,它的质量所占悬浮隧道整体结构的质量比例很小,可以忽略不计;
3) 悬浮隧道的弹性支座的阻尼系数为c1,同样它的质量也可以忽略不计;
4) 对于处在均匀流中的涡激振动下的悬浮隧道,只考虑它的一阶模态,其他的高阶模态在不很大影响最终计算结果的基础上予以忽略[10] 。
2.2. 悬浮隧道的动力平衡方程
均匀流中由于流体浮力和拖曳力作用下的,基于悬浮隧道结构实际的物理特性,它的挠度动力平衡方程[1] [11] 可以用下式表达
 (1)
(1)
式中 表示悬浮隧道管体在垂直流向的位移,
表示悬浮隧道管体在垂直流向的位移, 表示单位长度悬浮隧道的质量,
表示单位长度悬浮隧道的质量, 表示悬浮隧道的粘滞阻尼系数,
表示悬浮隧道的粘滞阻尼系数, 表示悬浮隧道的弹性刚度,
表示悬浮隧道的弹性刚度, 表示悬浮隧道的涡激升力,
表示悬浮隧道的涡激升力, 表示悬浮隧道在y方向上受到的流体阻尼力,
表示悬浮隧道在y方向上受到的流体阻尼力, 表示弹簧的弹力,
表示弹簧的弹力, 表示悬浮隧道支座处的阻尼力,l是悬浮隧道的长度,
表示悬浮隧道支座处的阻尼力,l是悬浮隧道的长度, 表示狄拉克函数。
表示狄拉克函数。
作用于悬浮隧道的涡激升力和y方向上的流体阻尼力可表示为[12] [13] :
 (2)
(2)
 (3)
(3)
式中 和
和 分别是拖曳力系数和升力系数,文中分别取
分别是拖曳力系数和升力系数,文中分别取 ,
, ,
, 为旋涡泄放频率,具体表达式见式
为旋涡泄放频率,具体表达式见式 。
。
由式(2)可知, 由两部分组成。我们可以对它的前一部分进行合理简化成
由两部分组成。我们可以对它的前一部分进行合理简化成 。将上式(2)和(3)代入式(1),式(1)可进一步简化成
。将上式(2)和(3)代入式(1),式(1)可进一步简化成
 (4)
(4)
式中流体附加质量 的表达式为
的表达式为 ,流体附加阻尼
,流体附加阻尼 的表达式为
的表达式为 ,
, ,
, ,
, 。
。
2.3. 悬浮隧道的边界条件
悬浮隧道的模型可以如图5进行简化,它的边界条件如下:
 (5)
(5)
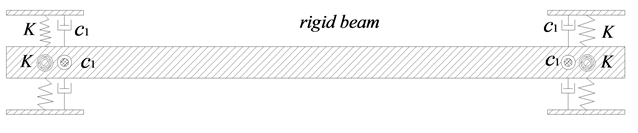
Figure 5. Calculation model of SFT
图5. 悬浮隧道的计算模型
2.4. 悬浮隧道的动力平衡方程的求解
根据相关假设,悬浮隧道管体的位移可写成如下形式
 (6)
(6)
式中 表示广义坐标,而
表示广义坐标,而 表示悬浮隧道的n阶振动模态的形状函数。如上述的假设,在分析均匀流中涡激振动作用下的悬浮隧道的动力响应中,这里只考虑它的一阶振动模态。
表示悬浮隧道的n阶振动模态的形状函数。如上述的假设,在分析均匀流中涡激振动作用下的悬浮隧道的动力响应中,这里只考虑它的一阶振动模态。
由于本文的首要目标是获得悬浮隧道位移的近似解,而忽略了的对悬浮隧道位移影响较小的高阶振动模态。这里将悬浮隧道的振动形式近似成梁的弹性位移的一阶模态形式和刚性梁的一阶模态形式的叠加。弹性梁和刚性梁均由弹簧和阻尼支撑。
悬浮隧道的一阶模态 ,如图5所示,它的表达式如下式
,如图5所示,它的表达式如下式
 (7)
(7)
式中, 的表达式为
的表达式为 ,代表悬浮隧道的弹性刚度EI对弹簧刚度K的比值。
,代表悬浮隧道的弹性刚度EI对弹簧刚度K的比值。
将式(6)代入式(4)中,方程两边同乘以 ,然后方程两边各自对悬浮隧道长度上进行积分
,然后方程两边各自对悬浮隧道长度上进行积分
 (8)
(8)
经过积分运算并化简后可得
 (9)
(9)
式中 ,
, 。
。
在式(9)中,悬浮隧道两端的阻尼力和弹簧的弹力的具体表达式可以用如下形式表达
 (10)
(10)
 (11)
(11)
式中的 是悬浮隧道两端的弹性支撑的阻尼系数。
是悬浮隧道两端的弹性支撑的阻尼系数。
把式(10)和(11)代入到式(9)中,式(9)可进一步简化成
 (12)
(12)
由于式(12)相对繁琐,为了便于计算,将其简写成如下
 (13)
(13)
式中
 ,
,
 ,
,
 。
。
前面式中出现的频率 的表达式为
的表达式为
 (14)
(14)
式中 表示简支形式的悬浮隧道的振动频率,
表示简支形式的悬浮隧道的振动频率,
 (15)
(15)
悬浮隧道的初始条件如下
 (16)
(16)
在上面给出的边界条件和初始条件,可以求解出广义坐标下的 ,
,
当 时,
时, 的形式如下:
的形式如下:
 (17)
(17)
当 时,
时, 的形式如下:
的形式如下:
 (18)
(18)
式中 ,
, ,
,
 ,
, 。
。
综上,将式(17)和式(18)分别代入到式(6)中,可得悬浮隧道一阶模态下的位移。
当 时,
时, 的形式如下:
的形式如下:
 (19)
(19)
当 时,
时, 的形式如下:
的形式如下:
 (20)
(20)
3. 悬浮隧道动力响应的模拟结果
3.1. 悬浮隧道的参数
由于当今世界上还没有一个实际投入使用的悬浮隧道,文中模拟采用的数据是位于中国浙江省千岛湖的悬浮隧道数据,此悬浮隧道在不久的将来可能会建成使用。但是,千岛湖中的水的流速较小,对悬浮隧道的影响不是很明显,这里对流速进行相应加大。
位于浙江千岛湖的悬浮隧道的模型的长度为100 m,隧道顶部位于水下的4.2 m深处。悬浮隧道各管段之间以及管段和湖岸之间的连接均为弹簧和阻尼连接,而隧道一端的轴向位移却是自由的。设计的悬浮隧道模型的横截面如图6所示,文中采用的悬浮隧道模型的参数[4] [14] 如表1所示。
在表1中悬浮隧道参数的基础上,对c1和K的变化及其对悬浮隧道的动力响应的影响进行研究。文中,通过计算给出一些c1和K的数值,c1的数值为3500 N/(m/s),10000 N/(m/s),20000 N/(m/s)和50,000 N/(m/s),K的数值为1000 N/m,3000 N/m和5000 N/m。
3.2. 模拟的结果
将表1中的参数代入式(19)和式(20)中,然后对不同取值的c1和K情况下,均匀流中涡激振动作用下的悬浮隧道的动力响应进行对比分析。取悬浮隧道管体跨中z = 50 m的动力响应数值模拟的结果如图7至11所示。
如图7到13所示,悬浮隧道跨中的位移随时间做周期性变化。由图7至图10,从中发现,对于c1 = 3500

Figure 6. Design cross-section of SFT
图6. 悬浮隧道模型的的设计截面
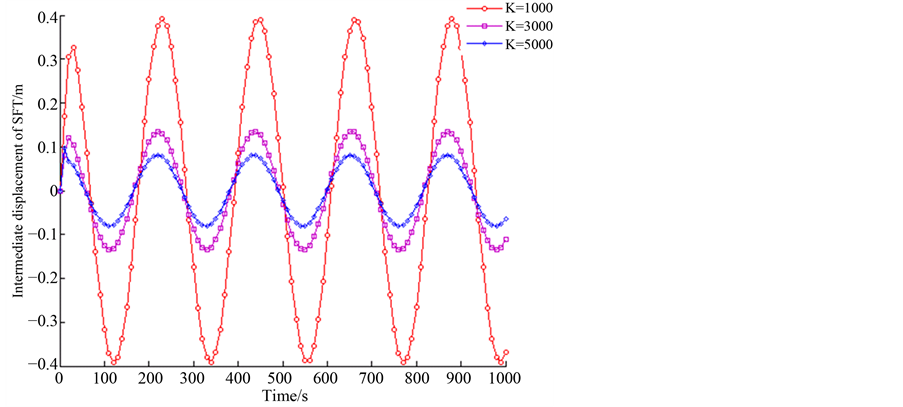
Figure 7. Dynamic response of SFTwhen c1 = 3500 N/(m/s)
图7. c1 = 3500 N/(m/s)时悬浮隧道时程动力响应

Table 1. Thebasic parameters of SFT
表1. 悬浮隧道基本参数
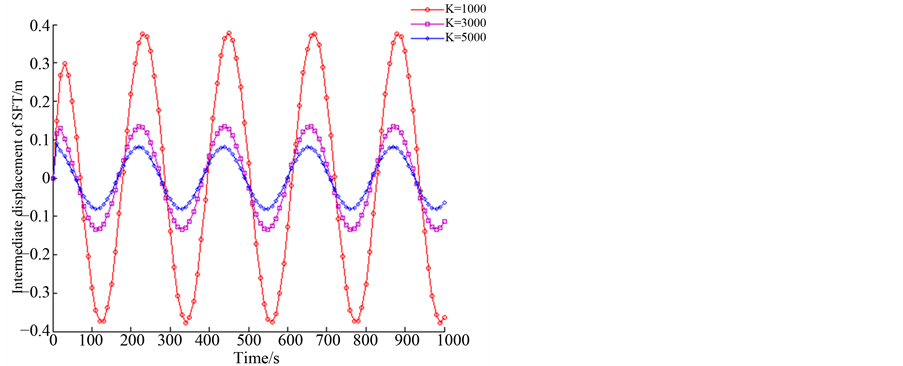
Figure 8. Dynamic response of SFT when c1 = 10,000 N/(m/s)
图8. c1 = 10,000 N/(m/s)时悬浮隧道时程动力响应
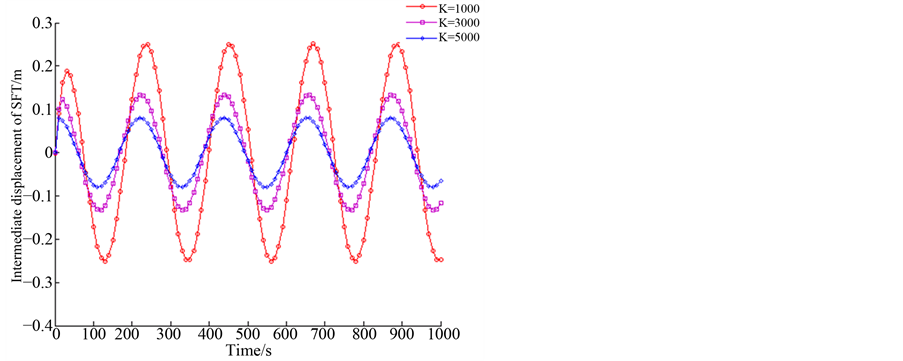
Figure 9. Dynamic response of SFT when c1 = 20,000 N/(m/s)
图9. c1 = 20,000 N/(m/s)时悬浮隧道时程动力响应

Figure 10. Dynamic response of SFT when c1 = 50,000 N/(m/s)
图10. c1 = 50,000 N/(m/s)时悬浮隧道时程动力响应
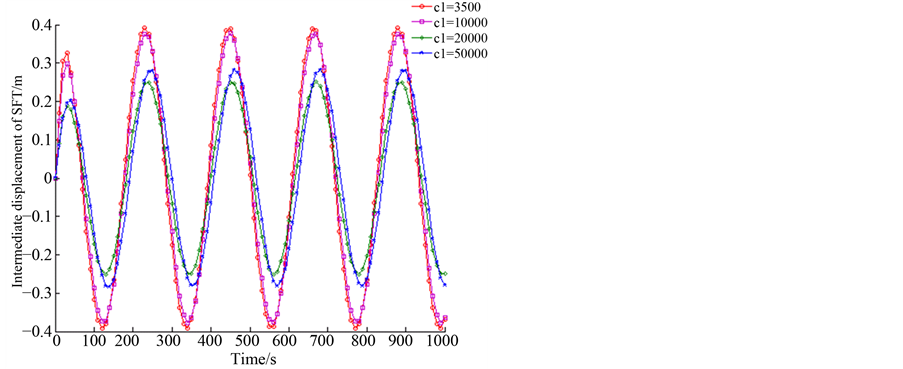
Figure 11. Dynamic response of SFT when K = 1000 N/m
图11. K = 1000 N/m时悬浮隧道时程动力响应
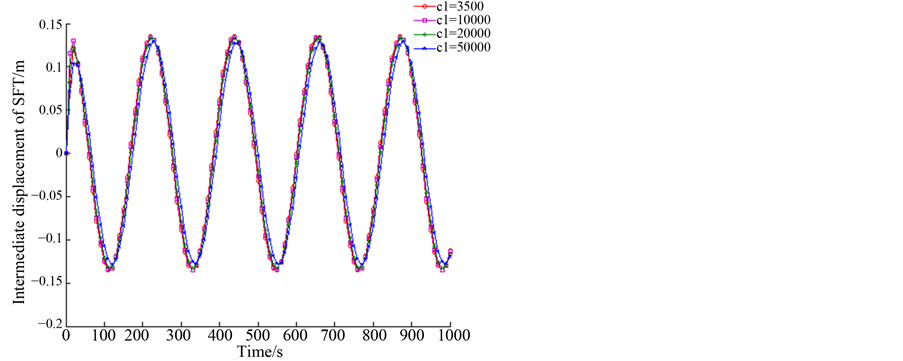
Figure 12. Dynamic response of SFT when K = 3000 N/m
图12. K = 3000 N/m时悬浮隧道时程动力响应
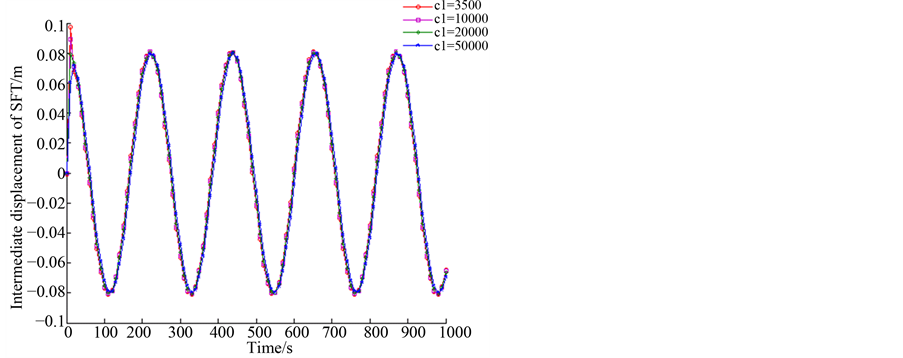
Figure 13. Dynamic response of SFT when K = 5000 N/m
图13. K = 5000 N/m时悬浮隧道时程动力响应
N/(m/s),c1 = 10,000 N/(m/s),c1 = 20,000 N/(m/s)和c1 = 50,000 N/(m/s)时,悬浮隧道跨中的位移的幅值随K值的增加而减小明显。当c1 = 3500 N/(m/s)和c1 = 10,000 N/(m/s)时,悬浮隧道跨中位移的幅值随着K值由1000 N/m增加到3000 N/m而由0.4 m降到0.15 m;当c1 = 20,000 N/(m/s)时,悬浮隧道跨中位移的幅值随着K值由1000 N/m增加到3000 N/m而由0.25 m降到0.15 m;当c1 = 50,000 N/(m/s)时,悬浮隧道跨中部的位移的幅值随着K值由1000 N/m增加到3000 N/m而由0.3 m降到0.15 m。当c1 = 20,000 N/(m/s)时,其他条件相同时,悬浮隧道的跨中位移幅值最小。
由图11至图13,由图显示,对于K = 1000 N/m,K = 3000 N/m和K = 5000 N/m时,悬浮隧道跨中的位移的幅值随c1值的增加而总体保持不变,但是随着K值的增加,c1的影响在减小。当K = 1000 N/m时,悬浮隧道跨中位移的幅值随着c1值由3500 N/(m/s)增加到50,000 N/(m/s)而由0.4 m降到0.25 m;当K = 3000 N/m时,悬浮隧道跨中位移的幅值随着c1值由3500 N/(m/s)增加到50,000 N/(m/s)而略微减小;当K = 5000 N/m时,悬浮隧道跨中位移的幅值随着c1值由3500 N/(m/s)增加到50,000 N/(m/s)而几乎不变。
通过以上对图7到图13的描述,从中可知K对悬浮隧道跨中位移由明显作用,而c1的作用较小。悬浮隧道跨中位移幅值随着K值的增加而显著减小,但是随着c1的变化跨中位移变化不是很明显,同时c1的作用随着的K值的增加而减小。
4. 结论
在本文中,悬浮隧道被简化成一个两端由弹簧和阻尼的弹性支撑梁。同时,对均匀流中涡激振动作用下的悬浮隧道的动力响应进行了分析和研究。最后,模拟了悬浮隧道支撑的弹簧刚度K值和阻尼c1值对悬浮隧道跨中位移的影响。从中得出的结论如下:
1) 悬浮隧道弹性支撑的阻尼c1对减小悬浮隧道跨中的位移幅值有微小作用。随着阻尼的增加,悬浮隧道跨中位移总体上几乎保持不变。只有当K值相对较小时,悬浮隧道跨中位移才会随着c1值的增加而减小。同时,c1值对悬浮隧道的影响随着K值的增大而降低。
2) 悬浮隧道两端弹性支撑的弹簧对降低悬浮隧道跨中位移的幅值有明显作用,跨中位移的幅值随着弹簧刚度K值的增大而明显降低。
3) 从上可知,在降低悬浮隧道跨中位移幅值的问题上,弹性支撑的弹簧比阻尼拥有明显的作用。
从以上的分析和讨论,可以得出悬浮隧道两端的连接的刚度直接决定了悬浮隧道的动力响应,而连接的阻尼却对悬浮隧道的动力响应几乎没有影响。所以,悬浮隧道锚固系统的刚度的设计和优化是今后值得深入研究的课题。