摘要:
根据地震波逆时偏移技术与常规克希霍夫和单程波深度成像技术的算法差异,开展了针对逆时偏移方法关键技术的若干问题分析。从理论模型的脉冲响应出发,理清了低频背景逆时噪声的成因机理,采用上下行波波场分离相关逆时成像条件实现有效压制;采用基于扩散滤波的拉普拉斯算子实现了低频背景逆时噪声的横向相对保幅压制处理,其效果要优于常规的高通滤波方法;对比分析了不同阶数声波方程1D逆时偏移处理的成像波形差异以及与克希霍夫结果的差异。计算结果表明,综合考虑逆时噪声和波形差异成因及其对应的解决方法,在实际陆地地震资料逆时偏移中取得了较好的应用效果。
Abstract:
According to the algorithmic difference between the seismic wave reverse-time migration technology and the conventional Kirchhoff integral method’s depth migration and one-way wave depth migration technology, we carry out several analyses of key problem on specific aspects of the reverse-time migration method. The paper starts from the theoretical model’s impulse response, and finds out the origin mechanisms of the low-frequency reverse-time noise, effectively weakening the low-frequency noise by using correlative reverse-time imaging condition with up/down going wave-field separation processing. The low-frequency reverse-time noise is eliminated afterward with relatively horizontal-amplitude preserved Laplacian operator based on diffusion filter, and this method’s processing effect is better than that of conventional high-pass filter method. What’s more, 1D reverse-time migration is carried out using different order acoustic wave equations together with 1D Kirchhoff depth migration. The computational results show that perfect application results are achieved in the reverse-time migration processing of practical land’s seismic data by considering the above factors.
1. 引言
逆时偏移技术是当前实现复杂构造高精度地震波偏移成像的重要技术之一。该技术采用双程地震波动方程,不需要对偏移算子进行上、下行波的波场分离处理,因此对地震波动方程的近似较少,适合于任意陡倾角、速度在横纵向变化较为剧烈情况的成像问题,能够解决单程地震波动方程偏移方法受倾角限制的缺陷和克希霍夫叠前深度偏移方法的多值走时问题[1] 。此外,地震波逆时偏移方法可以对多次波、回转反射波等通常认为是干扰波类型复杂波场进行准确成像,而克希霍夫深度偏移方法和单程波偏移方法均将多次波等波场当作一次反射波进行处理,这必然引入较大的误差。上述诸多优点正是当前地震波叠前逆时成像技术受到地球物理学界的高度重视并广泛推广应用的原因。随着计算机技术的快速发展,特别是基于CPU/GPU高性能集群并行计算技术和大容量磁盘的快速存储技术的出现,较大程度地改善了逆时偏移技术工业化应用的现状[2] 。
目前对地震波叠前逆时成像技术中的相关问题已开展了诸多研究,特别是如何提高逆时成像精度方面引起地球物理学界的广泛重视,这些研究成果主要包括叠前高保真预处理[3] -[5] (刘红伟等,2010;王童奎等,2012)、复杂构造层析反演和全波形反演等速度建模方法[6] -[8] (杨仁虎等,2010;Song等,2011)、逆时成像条件的改进[9] -[11] (Yoon等,2006;Antoine 等,2006;Liu等,2007;康玮等,2012)、逆时偏移后数据体的补偿和去噪处理[12] -[19] (Zhang等,2009;陈可洋,2011;陈康等,2012)等。在前人研究和实践的基础上,笔者针对逆时偏移技术中的若干问题进行了深入分析研究,以期提高对逆时成像技术的认识,并为实际地震资料的逆时偏移处理提供理论方法和应用依据。
2. 逆时偏移基本原理
这里以二维地震波动方程为例[13] :
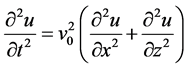 (1)
(1)
式中,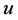 为质点震动位移,
为质点震动位移,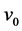 为地震波速度。
为地震波速度。
地震波逆时偏移主要包含震源波场正向传播(式(2))、检波点波场逆时延拓(式(3))、炮检点波场互相关
逆时成像(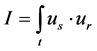 ,下表
,下表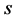 代表震源波场,
代表震源波场,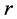 代表检波点波场)三个关键步骤,该技术的技术流程框图
代表检波点波场)三个关键步骤,该技术的技术流程框图
如图1所示,第2~第5小节对这些关键技术作逐一分析和论证。
我们对式(1)进行时域2阶、空域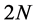 阶精度规则网格有限差分离散,得到
阶精度规则网格有限差分离散,得到
震源波场正向传播离散方程:
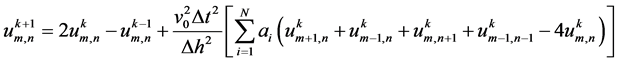 (2)
(2)
检波点波场逆时延拓离散方程:
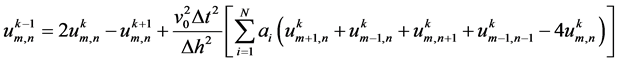 (3)
(3)
式中,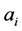 为高阶中心差分系数,
为高阶中心差分系数,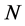 为空间差分阶数,
为空间差分阶数,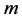 和
和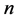 分别为
分别为 方向和
方向和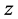 方向的空间采样点位置,
方向的空间采样点位置,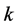 代表时间
代表时间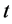 的采样点位置,
的采样点位置,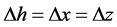 代表空间步长,
代表空间步长,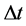 代表时间步长。从式(2)和式(3)可知,震源波场正向传播和检波点波场逆时延拓具有相似的离散计算公式,仅波场的延拓方向相反。在人工截断边界处,我们采用完全匹配层吸收边界条件[15] [16] ,以消除或削弱计算边界处的虚假反射波。
代表时间步长。从式(2)和式(3)可知,震源波场正向传播和检波点波场逆时延拓具有相似的离散计算公式,仅波场的延拓方向相反。在人工截断边界处,我们采用完全匹配层吸收边界条件[15] [16] ,以消除或削弱计算边界处的虚假反射波。
3. 低频噪声成因分析
低频、强能量的背景噪声是逆时偏移方法特有的成像特征,它的存在较大程度地影响了逆时成像剖面的信噪比和分辨率。低频噪声是逆时偏移在波场延拓和成像计算过程中产生的,通常归结为由内反射引起,但对具体的内反射形成机理目前仍不清晰,我们对比开展了深入研究分析。
图2为地震波逆时偏移成像过程分解示意图。常规相关法逆时成像条件可以表述为I1 = ①·③ + ①·④ + ②·③ + ②·④,其中·代表互相关运算,①代表下行震源波场,②代表上行反射震源波场,③代
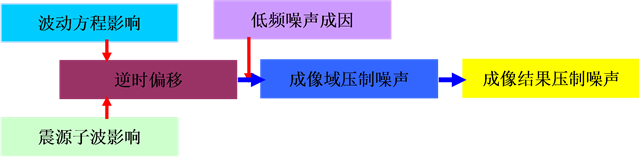
Figure 1. Flow map of reverse-time migration technology
图1. 逆时偏移技术的流程框图
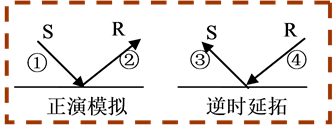
Figure 2. Imaging process decomposition schematic diagram of the reverse-time migration
图2. 逆时偏移中正演模拟和逆时延拓分解图