1. 引言
有限元法求解微分方程,由于可以对计算区域进行任意地剖分,更适合于复杂的计算域,因而在越来越多的实际计算中得到应用。在有限元法中,插值函数的选取是求解过程中关键的一步[1] 。它的选取由选择单元的几何形状以及近似函数的阶数来决定。本文结合王健平[2] [3] 提出的有限谱法,提出了一个新的有限谱插值基函数。它与待插值函数的形式无关,可在插值前先行求出。求解N-S方程时,随着雷诺数增加,对流项的非线性作用增强,容易出现数值解的失真震荡与迭代不收敛的现象。解决的方法之一是细分网格,降低单元网格的雷诺数,但是这样会增加计算时间并消耗内存。1976年,Christie[4] 等提出迎风有限元格式,对权函数进行修正。即增大节点上游方向的权函数,减小节点下游方向的权函数。1982年,Brooks和Hughes[5] [6] 通过在对流项上增加人工耗散来构造有限元的迎风格式。但是,相比有限差分法,要构造一个好的迎风有限元格式还需努力。1984年,Donea[7] 提出Taylor-Galerkin法,先对时间方向的变量做二阶或三阶的Taylor展开,把时间导数用空间导数来代替,然后再对空间变量用一般的Galerkin有限元法离散。由于这个方法隐含了流线迎风的耗散作用,又有固定的推导步骤,可以较好地应用于高雷诺数流动的计算。
2. 有限谱基函数
王健平[2] [3] 在谱方法的基础上提出了基于有限点,有限项的局域谱方法的概念,即有限谱法,要求近似函数有等间网格和非周期性的性质,解决了谱方法难以处理复杂计算区域和边界条件的问题。有限谱法的基础理论在于角频率空间和物理空间截断的非周期性傅立叶变换。有限谱基函数的物理含义是任意一点的影响主要在它的两侧的有限区域内。在它本身最大,向两端衰减。一点的近似值可以通过把相邻点在这一点的影响叠加而得到。
2.1. 一维有限谱基函数
 (2.1)
(2.1)
其中
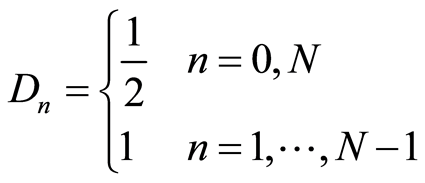 (2.2)
(2.2)
可以得到
 (2.3)
(2.3)
因此符合有限元基函数的要求。当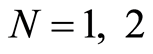 时,基函数形式分别为
时,基函数形式分别为
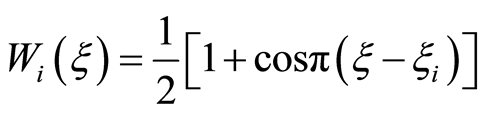 (2.4)
(2.4)
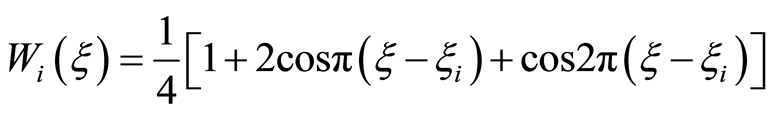 (2.5)
(2.5)
图1和图2分别是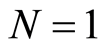 和
和 时一维一、二阶有限谱基函数。可见函数在原点为1,在其他节点为0的性质。
时一维一、二阶有限谱基函数。可见函数在原点为1,在其他节点为0的性质。
2.2. 二维有限谱基函数
2.2.1. 二维三角形单元
如同其他有限元法一样,引人无量纲面积坐标
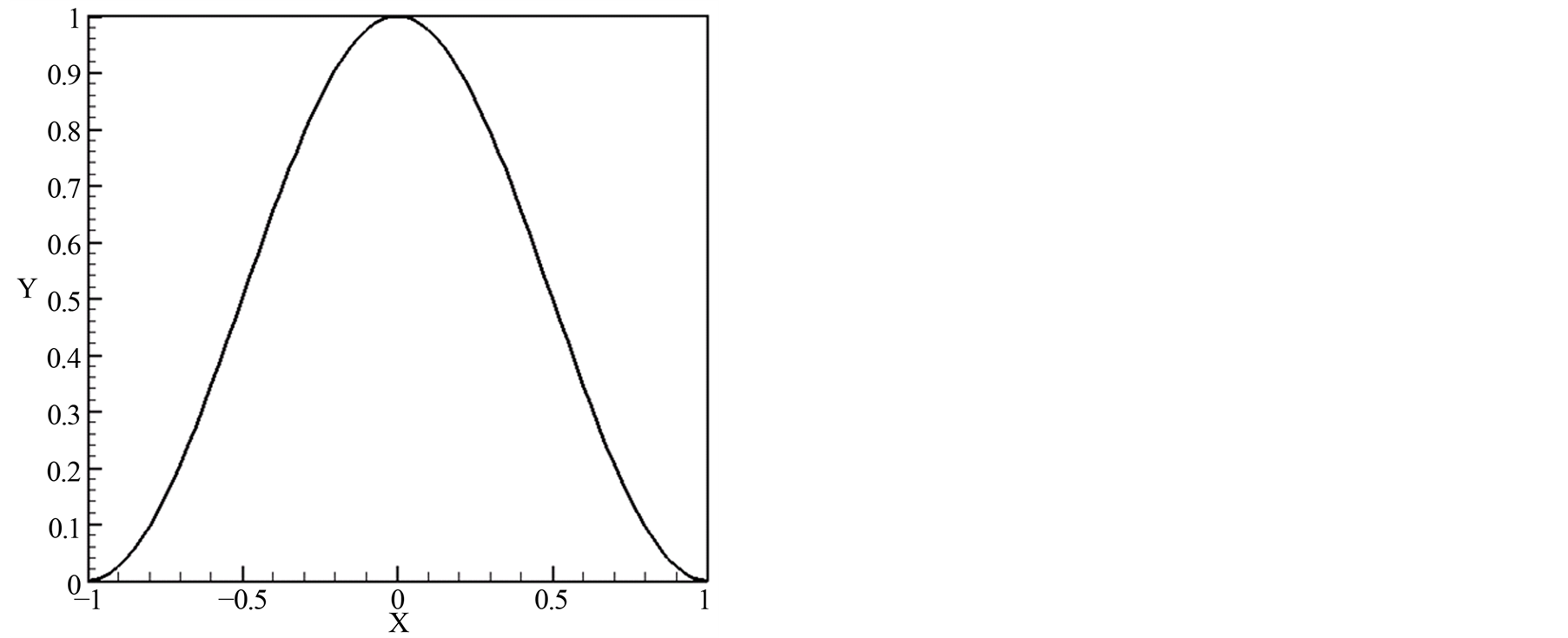
Figure 1. First-order finite spectral basis function
图1. 一维一阶有限谱插值基函数
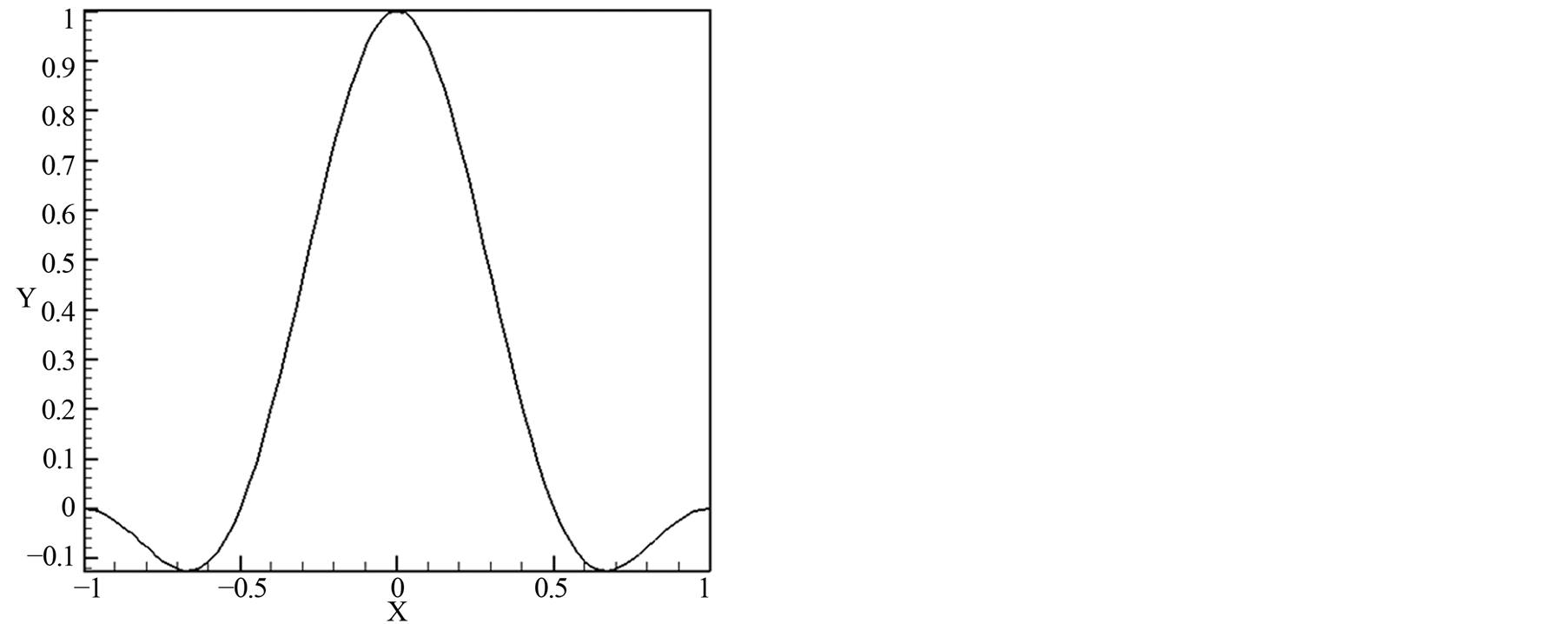
Figure 2. Second-order finite spectral basis function
图2. 一维二阶有限谱插值基函数
满足
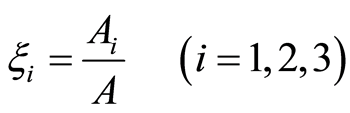 (2.6)
(2.6)
 (2.7)
(2.7)
面积坐标与直角坐标之间的关系为
 (2.8)
(2.8)
 (2.9)
(2.9)
一阶有限谱基函数为
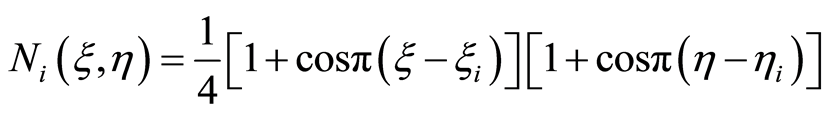 (2.10)
(2.10)
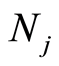 也取同样形式。
也取同样形式。
2.2.2. 二维四边形单元
坐标 和
和 之间的关系为
之间的关系为
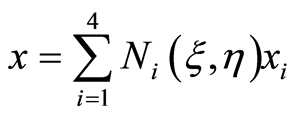 (2.11)
(2.11)
 (2.12)
(2.12)
二维有限谱插值基函数可表现为
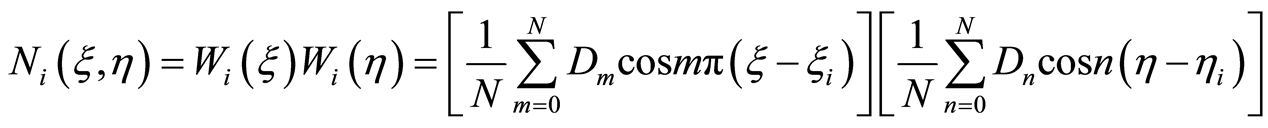 (2.13)
(2.13)
 同理可取同样形式。如图3所示,当
同理可取同样形式。如图3所示,当 时
时
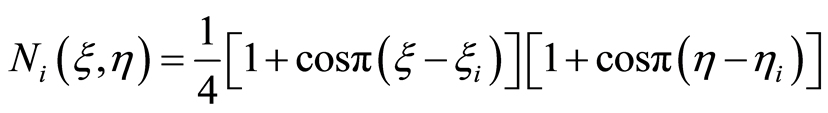 (2.14)
(2.14)
显然二维的有限谱插值基函数也满足
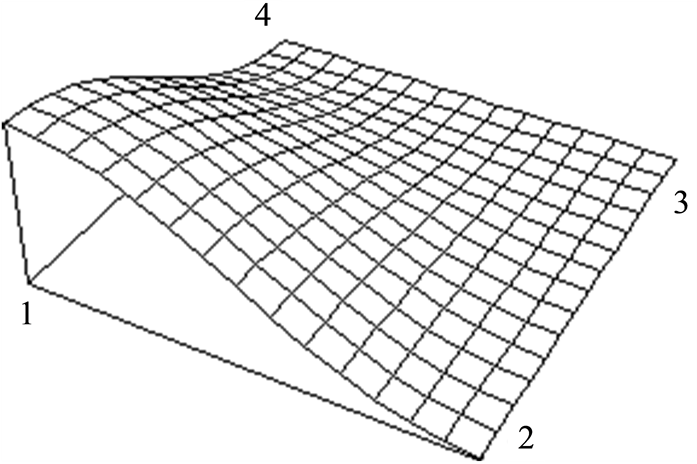
Figure 3. 2-D First-order finite spectral basis function
图3. 二维一阶有限谱插值基函数
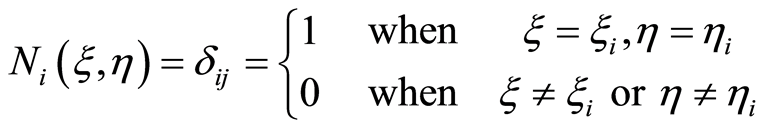 (2.15)
(2.15)
2.3. 有限谱法和差分方法的比较
分别用三阶有限谱法和三阶中心差分方法对波动方程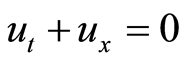 进行计算,初值条件为
进行计算,初值条件为
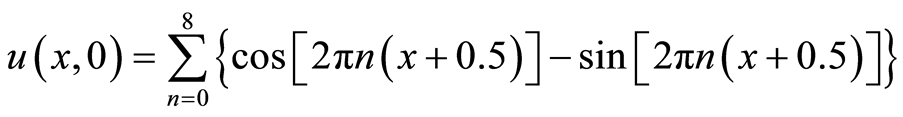 (2.16)
(2.16)
网格点数取为32。由结果可以看出,差分法会出现相位差,这是由于不同频率的成分传播速度不一样。而有限谱法可以避免这个问题。由此可见,有限谱法在计算含有波动的问题时要优于有限差分法(图4)。
3. 数值离散法
二维不可压缩流动的流函数–涡量方程为

式中, 是流函数,
是流函数, 是涡量,
是涡量, 为雷诺数,
为雷诺数,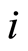 和
和 为Einstein下标
为Einstein下标
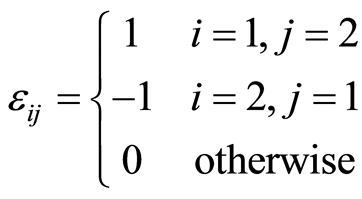
采用Taylor-Galerkin法处理式(3.2)
 (3.3)
(3.3)
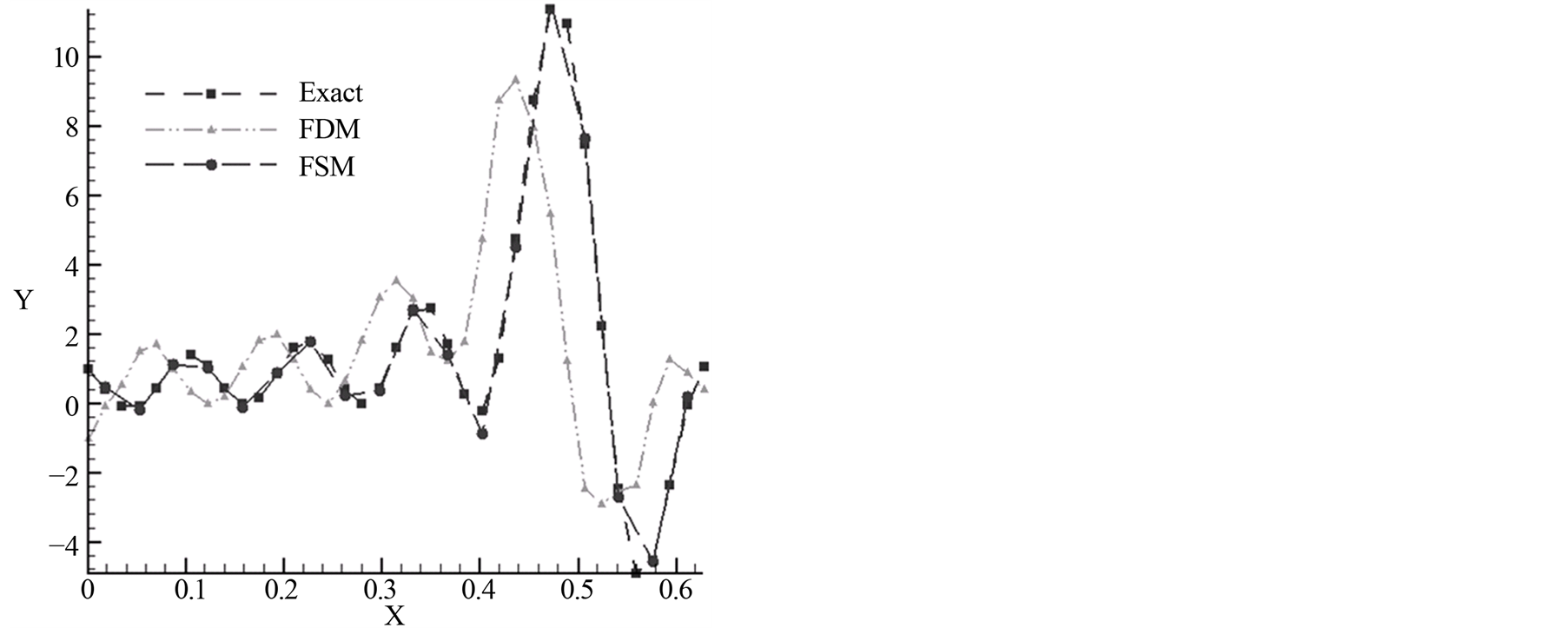
Figure 4. Comparison between exact solution and numerical solutions for wave equation by using thirdorder central spectral scheme and third-order central difference scheme
图4. 三阶有限谱法和三阶中心差分法计算波动方程结果与精确解的比较
先用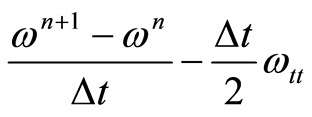 代替
代替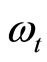
 (3.4)
(3.4)
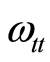 又可由式(3.2)得到
又可由式(3.2)得到
 (3.5)
(3.5)
把式(3.5)带入式(3.4),整理得
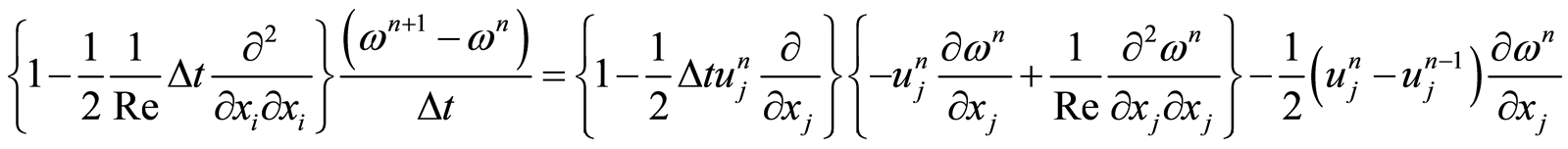 (3.6)
(3.6)
式(3.6)的有限元积分表达式为
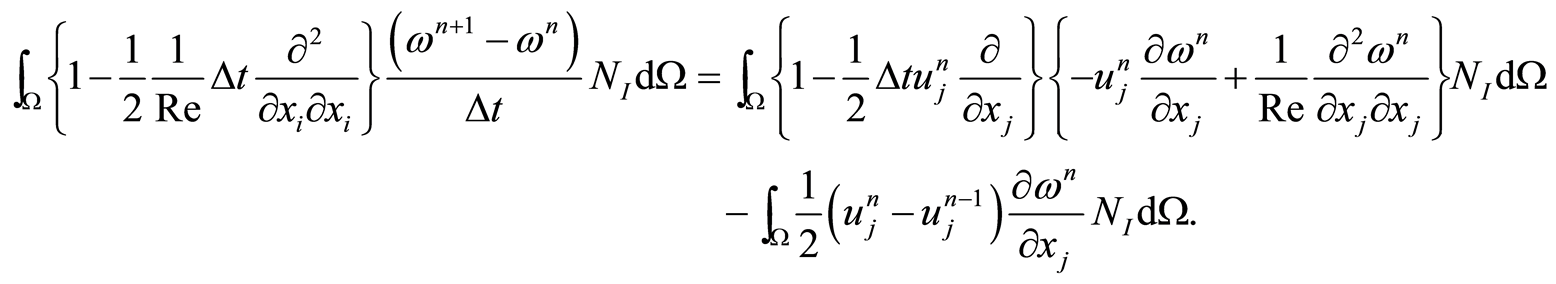 (3.7)
(3.7)
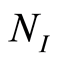 是权函数,令
是权函数,令 ,其中,
,其中, 为单元形函数,
为单元形函数, (
(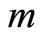 为单元节点个数),带入式(3.7)有:
为单元节点个数),带入式(3.7)有:
 (3.8)
(3.8)
其中:
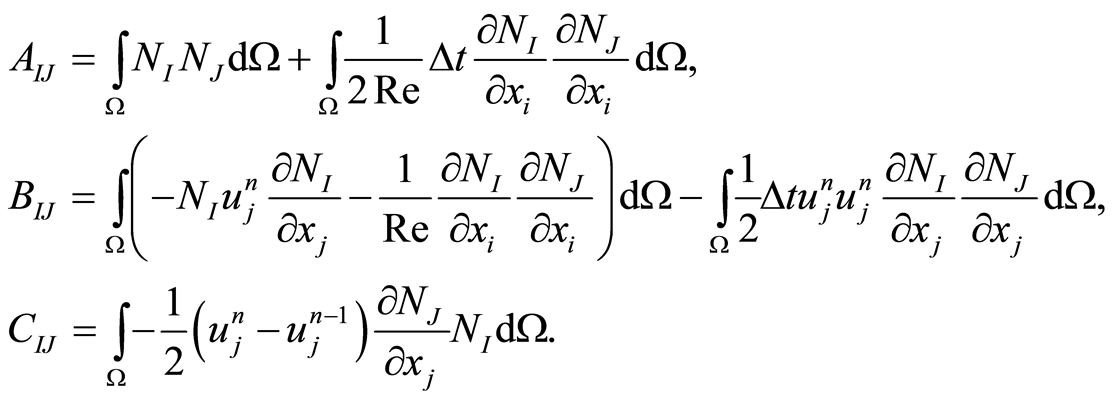
在计算域内将每个单元的有限元方程相加,合成总体有限元方程:
 (3.9)
(3.9)
此处,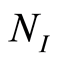 和
和 都取为有限谱插值基函数。
都取为有限谱插值基函数。
4. 计算结果与分析
方腔剪切流是一个有着典型流动现象和典型边界条件的流动问题。许多学者对它的流动规律做了包括实验和数值模拟在内的大量研究。因此它常常作为一个标准算例被用来检验数值方法的有效性。方腔流的上边界是以给定的速度运动,其余三个边界为固壁,上边界的运动带动腔内流体的流动。流动初始时刻,腔内的流体处于静止状态,开始流动后,由于流体有粘性,相邻的流体层之间相互作用,用快速液层带动慢速液层,慢速液层阻碍快速液层。
方腔流的形状和边界条件如图5所示。
4.1. 涡量的边界条件处理:(图6)
平板处的涡量: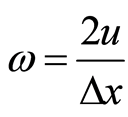
固体壁面处的涡量: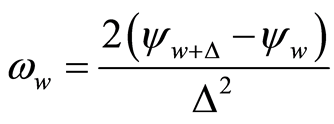 ,
,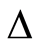 这里为
这里为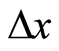 或
或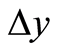
内凹角点D的涡量: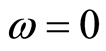
外凸角点C的涡量:取相邻点的涡量的平均值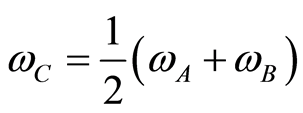
4.2. 计算结果分析
使用均匀网格,网格数为30 × 30,节点数为31 × 31,改变网格数对计算精度有较大的影响。利用上述边界条件对式(3.1)和(3.2)进行计算,时间步长为0.01 s,计算时方程的精度为 。
。
图7,8,9分别是雷诺数为100,1000和5000时的流线图,可以看出,雷诺数较小的时候,方腔的主涡涡心位于右上方,在底部的两角处各产生了一个较小的二次涡,两个二次涡的大小不等,右边的二次涡大一些。随雷诺数增加,底部的两个二次涡也随着增大,并且主涡涡心向方腔中心靠近。当雷诺数增大到5000时,左上角又产生了一个二次涡。
为了进一步与已有的结果进行对比,选用雷诺数100和1000两种情况的中线速度和已有的经典结果[8] 进行比较。通过对比,可以看出结果吻合比较好(图10,图11)。
5. 结束语
本文使用的有限谱基函数有以下优点:

Figure 5. Shape and boundary conditions of cavity flow
图5. 方腔流的形状和边界条件
Figure 6. Boundry handle for voticity
图6. 涡量的边界处理
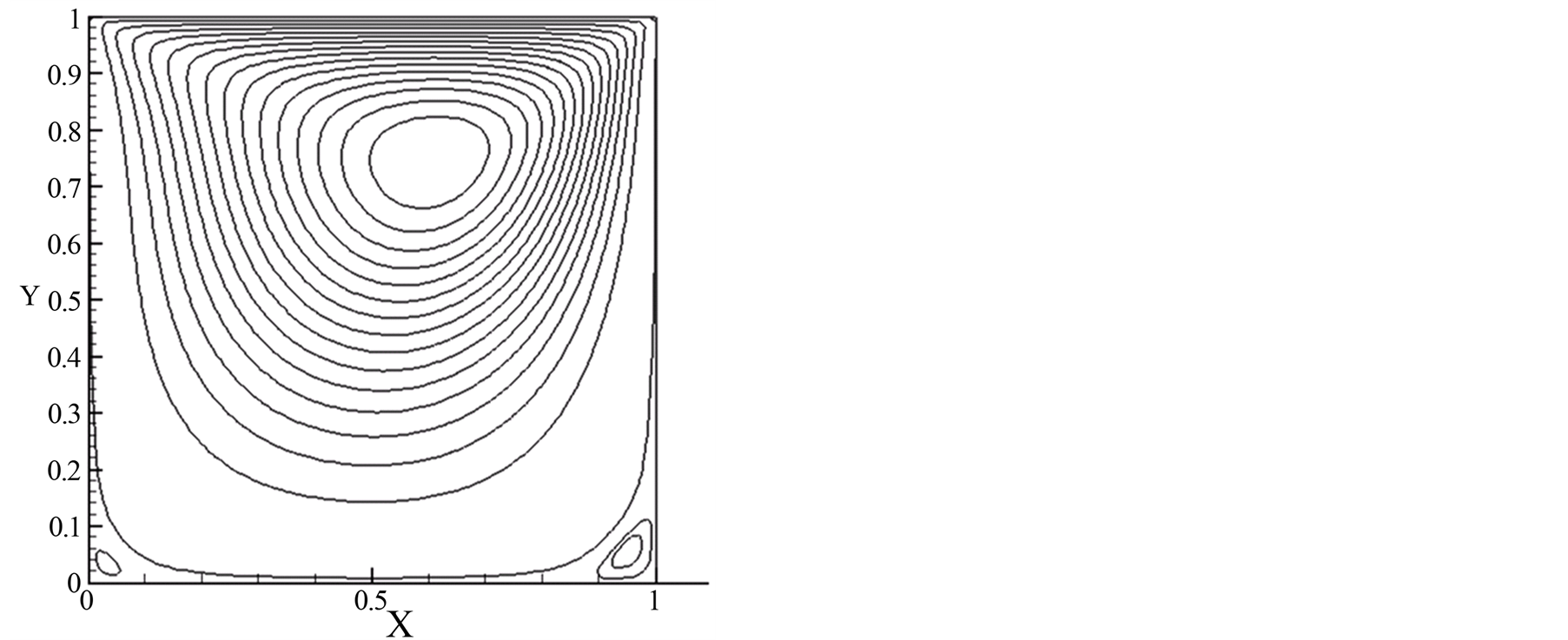
Figure 7. Streamlines, Re = 100
图7. Re = 100时的流线图
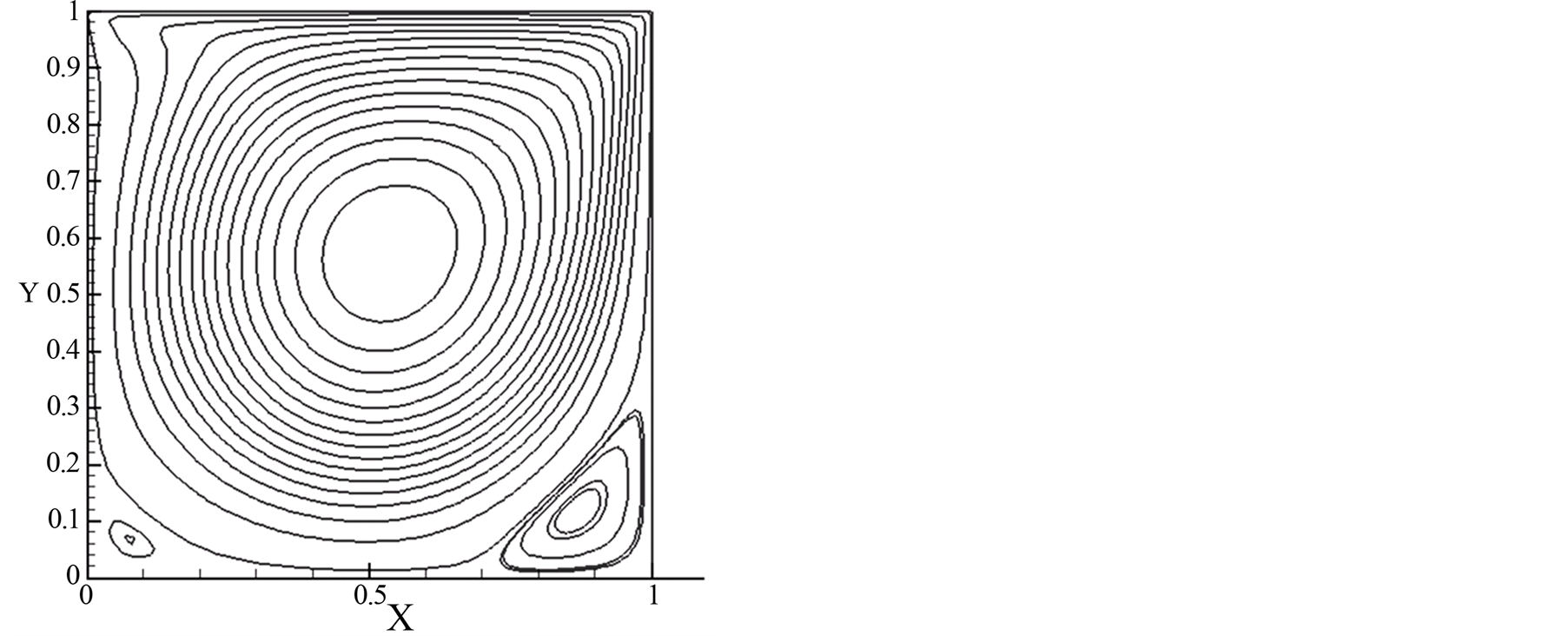
Figure 8. Streamlines, Re = 1000
图8. Re = 1000时的流线图
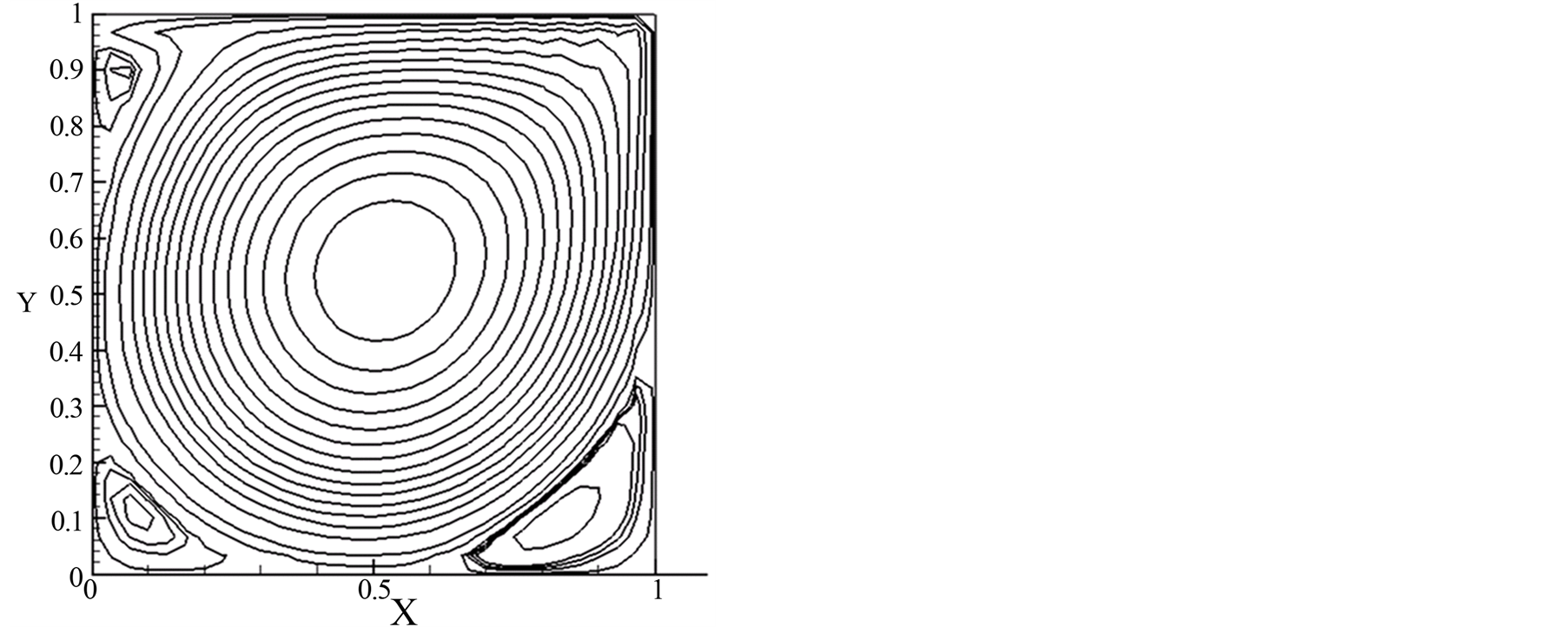
Figure 9. Streamlines, Re = 5000
图9. Re = 5000时的流线图
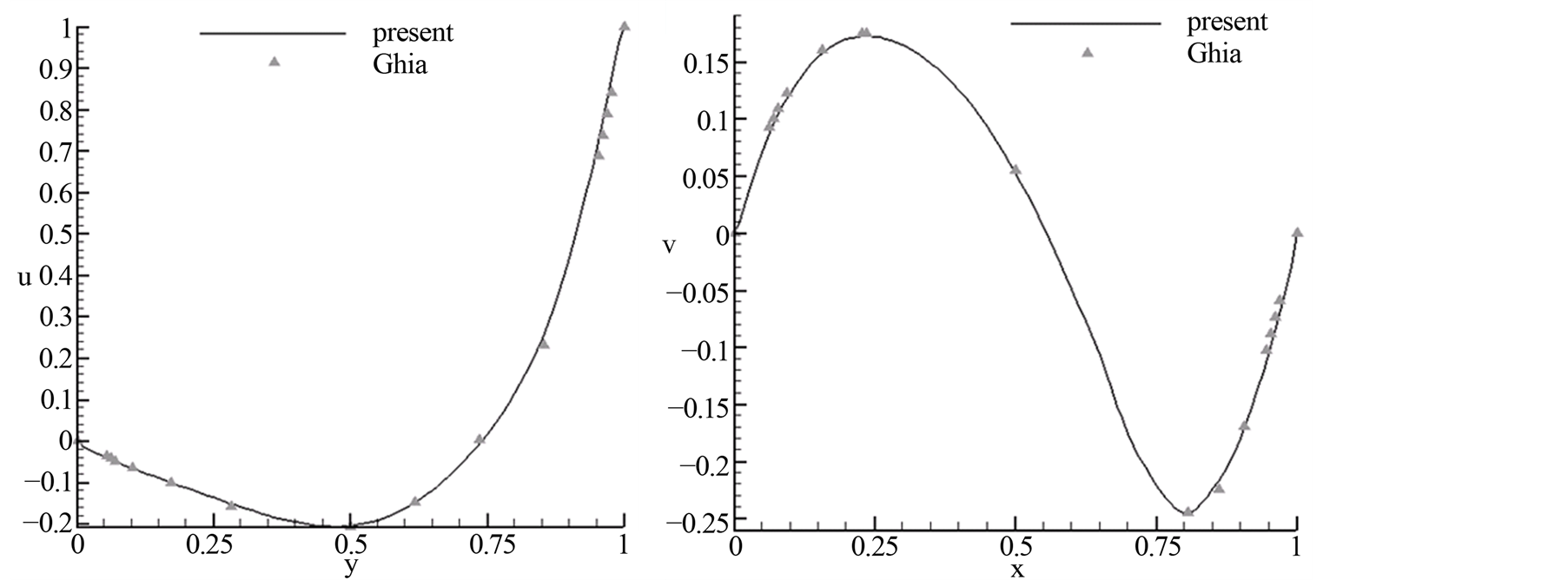
Figure 10. Center-line velocity (Re = 100)
图10. 中线速度(Re = 100)
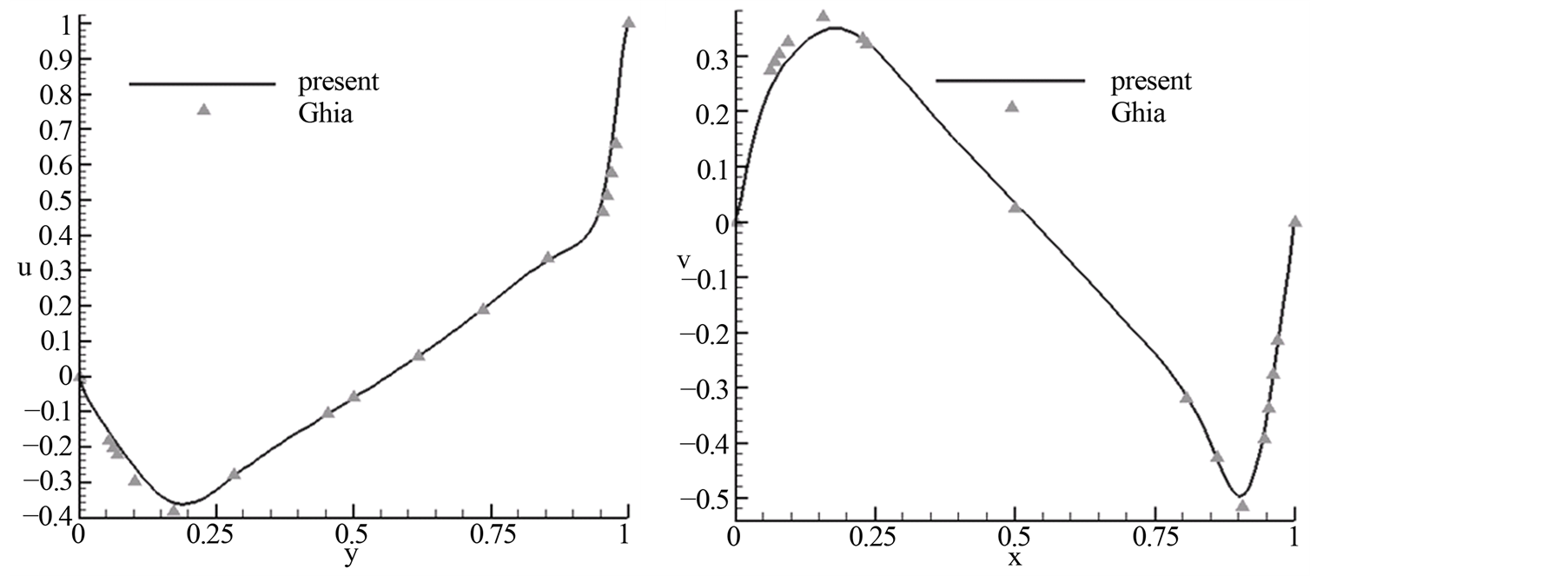
Figure 11. Center-line velocity (Re = 1000)
图11. 中线速度(Re = 1000)
1) 对于具有波动性质的函数,插值精度比拉格朗日插值基函数高,只需要很少的点就能够很好地模拟出原函数。
2) 基函数是无限光滑的三角函数的组合,无限可微,适用于湍流的高精度计算。
3) 形式简单,与待插函数形式无关。
本文使用有限谱基函数,推导出求解N-S方程的Galerkin积分表达式并通过计算方腔流来进行验算,得到了较好的结果,证实了此格式的适用性。