1. 引言
科学计算可视化、计算机动画和虚拟现实技术是现在计算机图形学领域研究的三大热点话题，而三维真实渲染技术是其中的一个核心技术[1] 。它被广泛的运用于卡通、游戏、电影、虚拟现实等工程领域[2] 。在当代社会中，电子书因为其相较于纸质书更加易于携带和保存，并且能够在黑暗的环境中阅读，越来越得到读者的青睐。常常可以见到这样的场景，在公交车上，许多乘客紧抓着他们的电子设备，不停的敲击触摸屏，看电子书。但是依然有很多狂热读者怀念纸张翻页时手指尖的触觉[3] 。
为了满足读者们的该项需求，计算机图形学界在纸张翻页仿真领域做了很多研究[4] 。大英图书馆发起了名为“大英图书馆的翻页”的先锋项目，旨在为读者提供更接近纸质书的电子阅读体验[5] 。他们拍下了图书馆所有书的每一页翻页时的照片，当读者阅读电子书要翻页时，则播放这些照片[6] 。这种方法的主要缺陷在与拍下图书的每页纸所费的时间是难以估量的。这种方法对于规模较大的在线图书管而言显然是不太现实的[5] 。
前人提出了几种其他的纸张翻页动作仿真建模方法。它们可以分成两类，基于几何的方法和基于物理的方法[7] 。
基于几何的方法忽略纸张实际的物理特性，通过指定一组几何方程来拟合纸张的外观，它们中的每一个都与一个特定的翻页动作相关。例如，一种动作是从底角翻起一张纸，而另一种则模拟纸张被折叠。当然，这样的用户动作的选择都有无限种，对于每一种做逐一定义外观方程是不可实现的。实际运用中，仿真应用可以对用户的选择做相应的限制。Beaudouin-Lafon提出了剥皮模型来解决二维纸张翻页仿真问题[7] 。将剥皮模型推广到三维，则形成了两种基于几何的三维仿真技术。一种是将纸张沿着圆筒卷曲，另一种是沿着圆锥卷曲。可惜的是，这两种方法的仿真效果看起来很僵硬。但是对于专心的看书的读者来说，这样的结果可以忍受。
基于物理的仿真方法能够得到比起几何方法更真实的效果。但是基于物理方法计算量也大得多。一种方法是质点弹簧系统。这种方法将纸看成一张由很多均匀分布的质点相互连接的网格。质点由理想化的没有质量的弹簧相互连接。遍历每根弹簧求出每个质点的受力情况后，通过一定的积分方法来得到质点的速度与加速度，由此得到翻页的仿真效果。设置的质点数量越多，则仿真效果越真实，但是会带来更高的计算量。另一种基于物理的方法是有限元方法[7] 。这种方法将纸张分割成相互连接的元素，进而计算每个元素的力、速度和加速度，按时间积分，得到翻页仿真效果。有限元方法是一种应用更加广泛的技术，这种技术的缺点在于比其他所有方法都要更耗时。因此对于实时仿真而言，有限元方法是不适用的。
本文的主要目标在与提高基于质点弹簧模型的纸张翻页仿真效果的表现。在本文中，我们将基于几何的方法与质点弹簧模型相结合，使得质点弹簧模型的仿真效果更加真实。曲面拟合技术被融入到模型中来减少计算量。之后我们记录下仿真过程中的关键帧信息，由此得到一个可重复而又快速的仿真效果。
本文的结构如下：第二章介绍纸张翻页仿真的框架与改进；第三章通过实验验证了这种新方法的有效性。第四章提出本文的结论与研究展望。
2. 纸张翻页仿真建模
在本文中，我们应用质点弹簧模型来对纸张建模。在本章，我们首先对经典的质点弹簧模型进行介绍，然后提出三项主要的改进。
2.1. 质点弹簧模型
质点弹簧模型(见图1)被广泛地运用于可形变软体的行为仿真。在这种方法中，一个软体被看作一些由理想化的无质量弹簧所连接的质点集。不同的弹簧可以设定不同的参数，并统一服从胡克定律。弹簧可以按照需要连接在任意两个质点间，而弹簧的受力原理也可以按需求设定。在仿真过程当中，遍历每一根弹簧并考虑阻尼力、重力和风力，得到每一个质点的受力情况。质点的运动服从牛顿第二定律，由此通过求解一系列的微分方程来解得质点的运动轨迹。欧拉法和龙格库塔法被用来求解这些微分方程。
阻尼力在振动系统中是一种能够限制、阻止减少振动的影响力。在质点弹簧系统中，阻尼力对与振动的质点施加与质点运动方向相反的作用力。阻尼力的大小与运动速度成正比。
在一个简单的软体仿真当中，由Provot提出的方法[8] ，质点由三种不同的弹簧相互连接，如图2。拉力、剪力和弯力弹簧。这些弹簧都可以设定相应的静止长度和弹性系数。这些弹簧可以用来分别模拟纸张的拉力、剪力和弯力。这些弹簧的弹性系数都可以根据需求来设置来得到理想的效果。
Figure 1. Mass-spring system
图1. 质点弹簧模型
Figure 2. The three types of spring
图2. 三种弹簧
在一个简单的质点弹簧系统仿真中，要得到质点的运动有三个步奏[8] 。第一步是遍历每一个弹簧并考虑风力、阻尼、重力，得到每一个质点的受力情况；第二步是应用牛顿第二定律得到每一个弹簧的加速度；第三步是通过选定的时间积分方法，得到每个点的新位置。重复以上的三个步奏，一个软体的仿真就得到了。
2.2. 改进
尽管简单的质点弹簧模型可以得到较好的仿真效果，但它是也忽略了纸张的材料特性。另一方面，当质点较多时，计算量消耗将会变得不可容忍。另外，当我们要一页接一页的重复翻页效果时，会产生一些不必要的计算量消耗。由以上三个方面的考虑，我们对基本的质点弹簧模型做了三项主要改进。
2.2.1. 同步
作为一种软体材料，纸张具有与布料等其他软体材料不同的特殊性质。想象一个纸筒，从纸筒的边缘来改变纸筒的形状比从上面改变要简单得多。当一片纸被弯曲时，它的形状看起来就想是一个圆筒，如图3所示。
因此我们假设从纸的底角处翻起并停在半空中时，翻起的纸张会显现出一种像“狗耳”的形状，狗耳的另外一面则是纸张的反面[7] 。如图4中所示，当纸张未被翻起时平行于狗耳线的其他线段，在纸张翻起之后，依然会保持平行的状态。而原本在一条平行线上的点，依然会保持在一条平行线上。例如，如图4所示，线段BE平行与线段SR。当纸张被翻起时，点B移动到点Q，点E移动到点T。因此线段QT应该仍然与线段SR平行。原本在线段BE上的点应该会移动到线段QT上。因此，线段BQ的长度和线段TE的长度应该一样，而与线段QT与线段BE的距离相等。基于以上的观察，我们在简单的质点弹簧模型中加入了一个新的步奏，同步。新的流程如下：
1) 遍历弹簧，计算质点的受力情况；
2) 应用牛顿第二定律，得到质点的加速度；
3) 基于用户选择的积分方法按时间步长积分，得到每个质点在下一个时刻的位置。
4) 根据每个质点在未翻页时的初始位置与狗耳线的距离分组，计算每个点现在位置与初始位置间的长度矢量；对于每一个同一组别的质点，平均这些矢量；最后得到同步后质点位置。
2.2.2. 插值
考虑到简单质点弹簧模型加入同步后，时间消耗增加了，因此减少质点的数量是有必要的。但是更少的质点也会时代仿真效果的真实性降低。为了平衡速度和真实性，我们运用了插值的办法。插值方法是将一定数量的点均匀的分布在质点旁边，然后通过运用合适的插值算法得到这些点的位置。
本文的模型中运用了拉格朗日插值方法[9] 。拉格朗日插值法的主要思想是基于一组数据点，建立插值函数，然后通过这个函数来求得空缺数据点的值。
在拉格朗日插值法中，假定[10] 是一组点集包含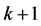
个数据的点集
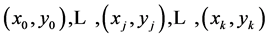，其中任意两个
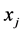不相等，其中拉格朗日形式的插值多项式是线性和
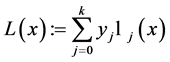，其中
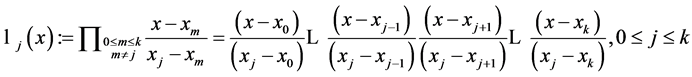
注意到，因为最初假定任意两个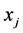
不相等，所以以上表达式是有意义的。若当存在
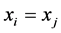时，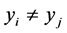
，则不会有插值函数
满足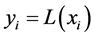
存在。对于每一个自变量
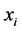，函数只能给出一个函数值。而如果存在
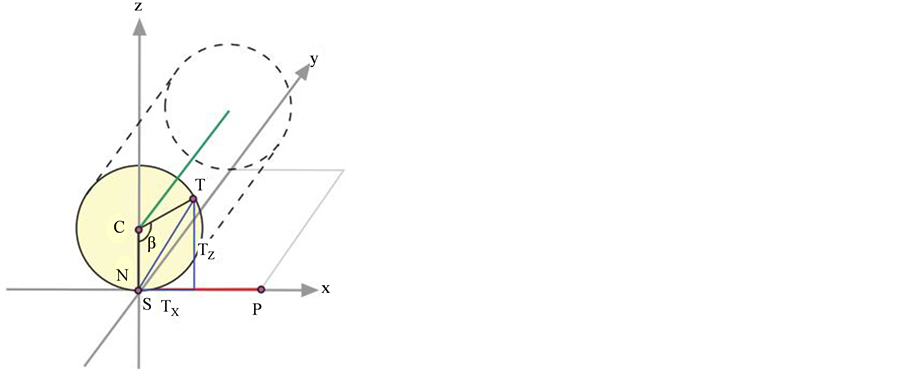
Figure 3. Curled paper 1
图3. 纸张弯曲示意图1
Figure 4. Curled paper 2
图4. 纸张弯曲示意图2
两个点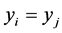
，则这两个点重合。对于任意的
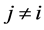，包含了算式
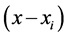，因此当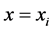
时整个算式将会等于零，而
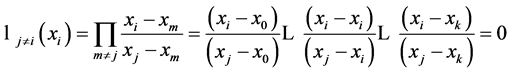
所以
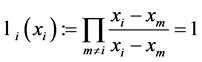
换句话说，其他的基多项式当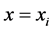
时都等于零，而
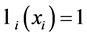，因为只有
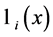中没有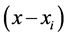
项。由此得出
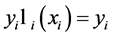，因此对于每一个点，
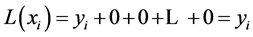，因此是准确的插值函数。我们只要将点的编号代入
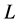函数中，就可以得到点在三维空间中的位置。
拉格朗日插值方法可以拟合出光滑的曲面。而因为本文中的质点数量相对来说比较小，所以我们并不用考虑龙格现象。同时拉格朗日插值方法是非常容易实施的。
2.2.3. 关键帧
有时，我们需要对于不同纸张重复进行同样一个纸张翻页的效果。因此，我们没有必要一次接一次的重复整个计算。考虑到这种情况，关键帧动画技术被应用到我们仿真方法中来减少不必要的计算消耗。
关键帧动画技术是一种经常应用于复杂模型动画的技术。它的基本思想是记录下一系列的动画关键帧信息，然后用合适的插值算法来得到在关键帧之间模型运动的运动状态。
3. 实验
本文的实验在32位Windows7操作系统下运行。计算机内存4 GB，CPU为i5-3230，主频2.6 Hz，显卡为GeForce GT 750 M。程序用C++写成，基于OpenGL，在Visual Studio 2008下运行。
3.1. 实验流程
实验流程如图5中所示。
1) 初始化模型：如图6所示，本实验的纸张由简单质点弹簧模型建模。在模型中，有36个平均分布的质点(红色打球)，这些质点由三种不同的无质量弹簧(拉力、剪力和弯力)相互连接。两个相邻的点之间的距离为5。在质点周围有676个平均分布无质量的点组成，这些点之间没有弹簧相互连接。每个质点所受的重力是0.00981。拉力、剪力和弯力弹簧的弹性系数均为1.0，阻尼系数为−0.7125。
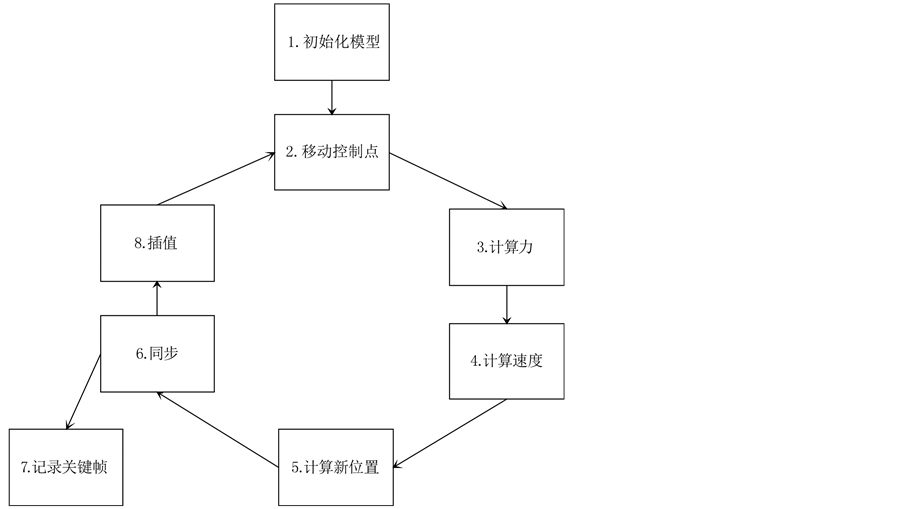
Figure 5. The flow diagram of our new page turning method
图5. 改进后纸张翻页仿真方法流程图
Figure 6. Model of page turning method
图6. 改进后纸张翻页仿真方法流程图
2) 移动控制点：选取页面的左边的6个点为控制点，持续移动这些控制点。页面右边的点为固定点；
3) 计算力：遍历每个弹簧，考虑重力和阻尼力，求得每个质点的受力。
4) 计算速度：应用半隐式欧拉法得到每个质点的速度。
5) 计算新位置：得到每一个质点新位置。
6) 同步：取得每个狗耳线的端点，将每个质点按照他们初始位置与狗耳线的距离分组；接下来，对于每一组质点，计算它们现在位置到原有初始位置的位移矢量，同步这些矢量，得到每一个质点新的位置。
7) 记录关键帧：每0.1秒记录下每个质点的位置。当要重复一个翻页仿真效果时，我们可以运用简单的插入算法得到同样的仿真效果，由此节省了时间消耗。
8) 插值：用拉格朗日插值算法，得到每个在质点周围的插入点的位置。
3.2. 实验结论
仿真的效果如图7所示。
由图可知，仿真的视觉效果是令人满意的。而仿真的速度也较快。我们重复进行了10次实验，并记录下每一次的时间消耗，如表1所示，通过应用关键帧技术，平均的时间消耗可以减少18%。
4. 结论与展望
在本文中，我们通过对传统的质点弹簧模型进行了3项改进，提出了新的三维纸张翻页仿真方法。三项主要的改进分别是：同步、插值和关键帧。通过在实验中实施这些改进，得到了比原有的传统的质点弹簧模型更加真实的仿真效果。另一方面，我们的仿真方法因为采用插值算法减少了质点的数量提升了运行的速度。另外，通过运用关键帧技术，我们可以更有效的重复一个翻页仿真的效果，避免了重复的计算。
在未来的研究中，更加快速的插值算法可以更好的减少运算量并得到更真实的仿真效果。更加具有挑战性的仿真项目是纸张折叠和纸张撕裂。这些研究方向对于计算机图形学界依然是不小的挑战。
Figure 7. The results of the experiment
图7. 翻页仿真实验效果图
Table 1. The time consumption (Unit of time in milliseconds)
表1. 纸张翻页仿真实验时间消耗(单位：毫秒)
致 谢
感谢曾亮老师对该论文研究的指导。