1. 引言
联合国气候变化政府间专门委员会IPCC (International Panel on Climate Change)第五次发布的特别报告指出,大量观测资料表明,最近60年无论是在全球尺度还是区域尺度上,降水、气温还有极端事件发生频率等方面都发生了显著变化[1] 。张利平等把极值定义为在给定的时期内,或该时期的一定月份或季节内观测到的水文要素的最高值或最低值[2] 。但在现代极值理论研究中,不同的建模方法对可以作为极值的观测数据有不同要求[3] 。目前,极端水文事件是国内外研究的一个热点问题,而作为重要影响因子之一的降雨量的极值变化特征研究也在相关领域得到关注和重视。翟盘茂等利用中国296个分布均匀的测站的逐日降水资料,研究了中国过去45年中降水量、降水频率、降水强度等方面的极值变化趋势[4] ;黄琰等从极值概率角度研究了中国极端气温和降水的空间分布随时间变化的情况[5] ;姜彤等运用广义极值分布、广义帕累托分布、广义逻辑分布和韦克比分布等4种分布函数定量拟合了长江流域降水极值的概率分布[6] ,都促进了极值理论在降水极值变化趋势分析方面的应用,但这些研究多采用最大值系列作为样本进行分析,而忽略了时段内发生的其他独立极值样本。本文拟基于超定量系列建立降雨极值分析模型,并以汉江流域为例,通过探讨汉江流域降雨极值的时空分布规律和统计概率特征,为进一步深入研究气候变化对汉江流域极端事件的影响提供一些思路和参考。
2. 研究区概况
汉江是长江中游最大的支流,流域面积约15.9万km2,干流全长1577 km,流经陕西、湖北两省,于武汉市注入长江。汉江干流根据其河道特点,分为上、中、下三个河段,丹江口以上为上游,河段长925 km,占汉江全长的59%,控制流域面积9.52万km2;丹江口至钟祥碾盘山为中游,全长270 km,占汉江全长的17%,区间流域面积4.68万km2;碾盘山以下为下游,长382 km,占汉江总长的24%,集水面积1.7万km2。
汉江流域处于东亚副热带季风区,其降水主要来源于东南和西南两股暖湿气流。汉江流域多年平均降水量为904 mm,折合降水总量为1399.5亿m3,占长江流域降水量的比重约为7%。由于纬度和地形条件的差异,年降水量呈现南岸大于北岸,上、下游大,中游小的地区分布规律,流域内多年平均降水量为700 mm~1800 mm。汉江上游年内降水有三个集中时段:4月下旬至5月下旬为春汛,6月下旬至7月下旬为夏汛,8月下旬至10月为秋汛,其中夏汛时段雨量最大,秋汛次之,但遇降雨天气有异时,秋汛雨量也会超过夏汛。相比而言,下游地区春汛、秋汛主峰不如上游明显。流域降水年内分配不均匀,5~10月降水占全年的70%~80%,7月、8月、9月这三个月的降水量占年降水量的40%~60%,年降水量系列Cv值上游地区为0.20,中、下游地区为0.25 [7] 。
本次采用汉江流域15个气象站1961~2010年共50年的逐月降水系列进行降雨极值特征分析,站点分布见图1。
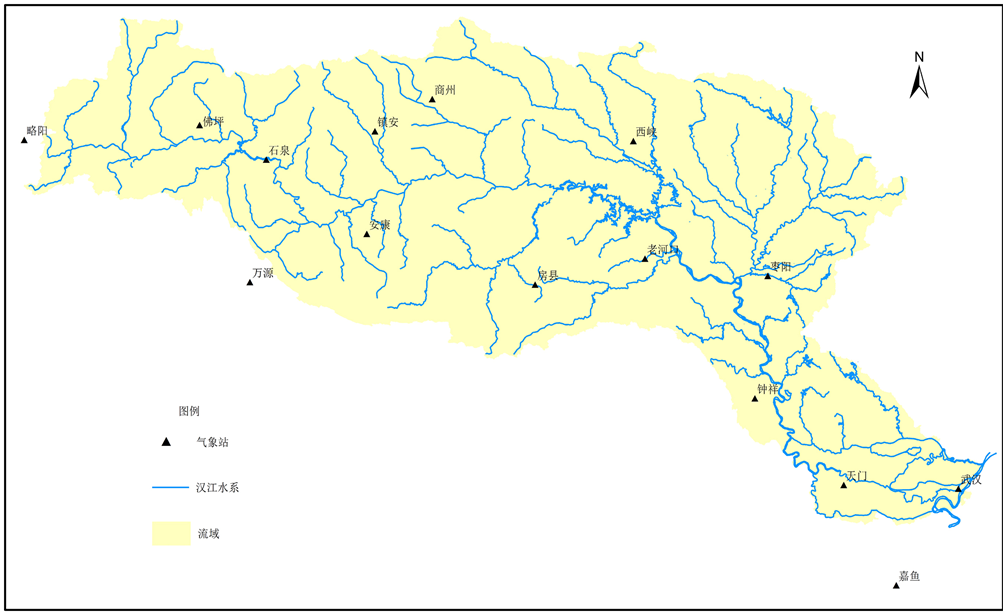
Figure 1. Spatial distribution of the meteorological stations in Han River basin
图1. 汉江流域气象站点分布示意图
3. 模型与方法
3.1. PDS/GP模型
PDS (Partial Duration Series)在水文上也称为超定量POT (Peak Over Threshold)系列[8] ,超定量系列样本数为超定量发生次数[9] 。经典的PDS模型假定:① 超定量发生次数服从Poisson分布;② 超定量样本独立;③ 超定量样本服从指数分布(EXP)。但是,近十几年的研究表明,PDS超定量样本符合GP (General Pareto)分布,指数分布只是其特例。因此,本文采用PDS/GP模型[10] 分析汉江流域降雨极值特征。由于本次所用资料系列的时间尺度为月,根据Willems等的研究[11] -[13] ,可认为样本满足独立性条件。
按照基本假定1,单位时间t内发生n次超定量的概率服从Poisson分布,即有:
 (1)
(1)
式中,λ为单位时间内超定量平均发生次数。
符合GP分布的PDS模型表达为[14] :
 (2)
(2)
式中,σ为尺度参数,ξ为形状参数,u为选定的阈值。
3.2. 阈值选取
由于阈值选取的重要性,已经有很多文献对此进行了讨论[15] -[17] 。但最常用的方法仍然是平均超出量函数(或称平均剩余寿命函数)法,即确定一个关于u的线性函数e(u):
 (3)
(3)
对于给定的样本 ,定义样本的超出量函数为:
,定义样本的超出量函数为:
 (4)
(4)
式中,Nu为超出量的个数, 表示超过阈值u的观测值的下标集合。如果u0是适当的阈值,则对大于u0的u,en(u)的斜率将保持不变。
表示超过阈值u的观测值的下标集合。如果u0是适当的阈值,则对大于u0的u,en(u)的斜率将保持不变。
另外一种选取u的常用方法是判断u值改变引起的参数估计量的变化,即在一个u值取值范围内,利用超出量估计σ和ξ。由于σ的估计值是u的函数,有必要对其进行修正,令σ*为修正的尺度参数,并有:
 (5)
(5)
当u > u0时, ,带入式(5)可以得到:
,带入式(5)可以得到:
 (6)
(6)
此时可以发现,修正的尺度参数σ*已经与u无关。因此,如果u0是适当的阈值,相应的超出量服从GP分布,则对大于u0的u,相应的σ*和ξ的估计量将保持不变。
本次将上述两种方法结合使用来选定合适的阈值,并通过拟合残差平方和最小的方法来减小主观定性判断选取阈值的不确定性。此外,为了充分体现PDS/GP模型预测极值的优越性,在阈值选取时确保每年至少有一个数据。
3.3. 参数估计
GP分布常用的参数估计方法有矩法(MOM)、极大似然法(ML)、概率权重矩法(PWM)、线性矩法(L-M)等。综合比较各种方法的适用性和优劣后,本次选用ML方法进行参数估计。
对于满足GP分布的超定量样本分布函数,其对数似然函数为:
 (7)
(7)
式中符号意义同上。使函数L达到最大的σ和ξ即为参数的极大似然估计 和
和 。
。
4. 结果和讨论
4.1. 统计特征初步分析
分析近50年的资料,汉江流域15个站点的最大月降雨量除了嘉鱼站出现在1964年,其它均出现在80年代以后,直方图显示样本序列均为非正态分布。从图2可以看出,有11个站点的峰度系数大于3,表明所采用的资料系列具有明显的尖峰厚尾特征;在所有站点中,武汉站具有最大的极差值,万源站次之。(受篇幅限制,本次仅在上、中、下游各取一个代表站显示结果)。
4.2. 降雨极值分析
根据式(4)计算各站降雨系列在不同阈值下的平均超出量,并绘制平均剩余寿命图(图3,红线标注可能合理
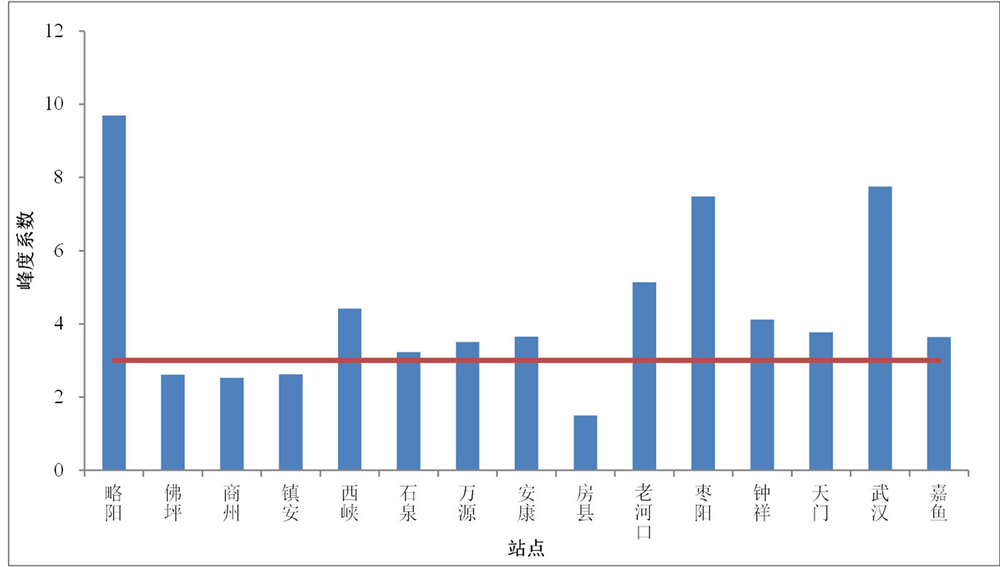
Figure 2. Kurtosis of monthly rainfall series at each station in Han River basin
图2. 汉江流域各站点降雨系列峰度系数比较图
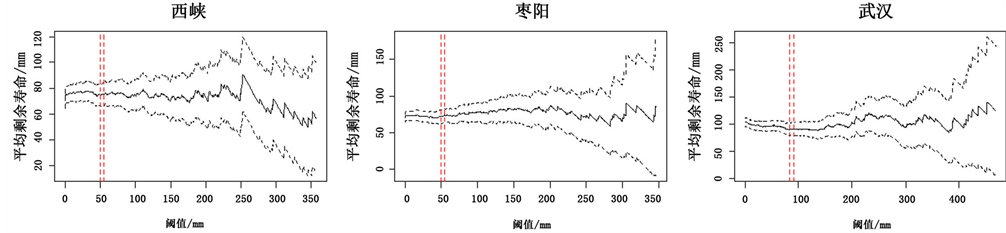
Figure 3. Average residual life plot of monthly rainfall at representation stations in Han River basin
图3. 汉江流域代表站月降雨平均剩余寿命图
阈值区间,黑色虚线为95%置信区间)。根据15个站点的平均剩余寿命图,进一步确定平均超出量与阈值大致呈线性关系的区间。由于近似线性为定性判断,存在一定误差,本次通过取残差平方和最小的方法进一步缩小阈值的取值范围,提高阈值选取的稳定性。以武汉站为例,当阈值在[83, 112]区间时,平均超出量与阈值大致呈线性关系,进一步将该区间内的数据升序排列后划分为3个子区间,分别为[83, 92]、[93, 102]和[103, 112],并求出每一组数据中的第一点和最后一个点连成的直线的斜率,然后求出每一组数据对该直线的拟合残差平方和,最后选取拟合残差值最小的[83, 92]区间为可能合理阈值区间。用同样的方法可确定其它站点的可能合理阈值区间,结果详见表1。
在平均剩余寿命图确定的可能合理阈值区间基础上,根据模型的尺度参数和形状参数估计值随阈值的变化情况,找出参数估计值稳定不变的区间。最后利用每个可能的合理阈值计算得到相应的参数估计值,并通过模拟检验找出模拟效果最好的阈值及相应阈值下的 和
和 。
。
以武汉站为例,在第一种方法确定的[83, 92]区间内, 和
和 值在[85.5, 92]区间内基本保持不变(图4,蓝线
值在[85.5, 92]区间内基本保持不变(图4,蓝线

Table 1. Reasonable threshold and corresponding parameters
表1. 最终确定的合理阈值及相应参数估计值
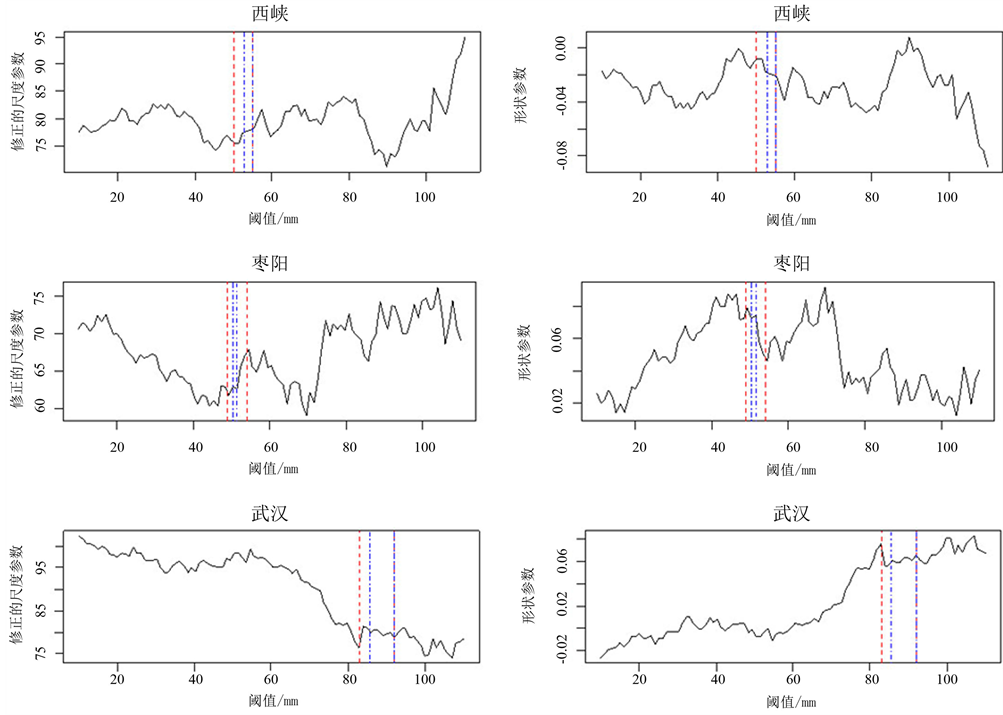
Figure 4. Change of modified scale and shape parameters with the threshold at representative stations
图4. 汉江流域代表站模型参数随阈值变化情况图
标注可能合理阈值区间),此时可确定19个可能成为合理阈值的月降雨量。通过比较发现,当阈值为85.5时,模型模拟效果最好(图5),相应的 和
和 分别为85.741和0.058,标准误分别为7.378和0.062。尺度参数估计值的标准误较大表明超过阈值的月降雨量波动较大。由实测资料分析,武汉站超阈值样本的最大值与最小值之比为8.83,说明参数估计值符合实际情况。用同样的方法可确定其它站点的合理阈值以及相应的参数估计值,结果详见表1。
分别为85.741和0.058,标准误分别为7.378和0.062。尺度参数估计值的标准误较大表明超过阈值的月降雨量波动较大。由实测资料分析,武汉站超阈值样本的最大值与最小值之比为8.83,说明参数估计值符合实际情况。用同样的方法可确定其它站点的合理阈值以及相应的参数估计值,结果详见表1。
4.3. 重现水平估计
随机变量x的T年重现水平为:
 (8)
(8)
式中,u0为选定的阈值,T为重现期,其他符号意义同上。
根据式(8)计算了各站点不同重现期的月降雨极大值,并利用Kriging方法进行空间插值(图6),从图中可以看出,汉江流域月降雨极值分布的空间差异性较大,总体看来呈下游大、上游其次、中游最小的分布趋势。受极大值影响,相同重现期下万源、武汉、嘉鱼站的月降雨极值预测结果远远大于其他站点。由于本次所采用的资料系列较短,随着重现期的增大,模型预测的不确定性逐渐增加。通过将15个站的计算结果取平均求得汉江流域20年、50年、100年和200年一遇的月降雨极值分别为403.3 mm、462.4 mm、506.0 mm和548.8 mm。
4.4. 与AM/PIII模型的对比分析
为了分析PDS/GP模型的可靠性,本文将模型估计结果与采用年最大月降雨量系列的PIII型分布(AM/PIII)的计算结果进行了对比(见图7)。分析发现,相同重现期下AM/PIII模型的计算结果普遍大于PDS/GP模型预测值。以武汉站为例,PDS/GP模型预测的20年、50年、100年和200年一遇月降雨量分别为550.3 mm、656.5 mm、740.7 mm和828.4 mm;AM/PIII模型预测的20年、50年、100年和200年一遇月降雨量分别为562.3 mm、671.3 mm、752.7 mm和833.5 mm,比前者增大12.0 mm、14.8 mm、12.0 mm和5.1 mm。但总体看来,差别不是特别明显,这一方面是因为研究流域内各站点的月降雨极值年际变化和空间差异较大,另一方面则与本次研究所采用的资料序列过短有关。
5. 结论
(1) 汉江流域15个站点的50年逐月降雨量系列统计参数表明,资料系列具有明显的尖峰厚尾特征,选用合
 (a) 西峡站 (b) 枣阳站 (c) 武汉站
(a) 西峡站 (b) 枣阳站 (c) 武汉站
Figure 5. Change of modified scale and shape parameters with the threshold at representative stations
图5. 汉江流域代表站模型参数随阈值变化情况图
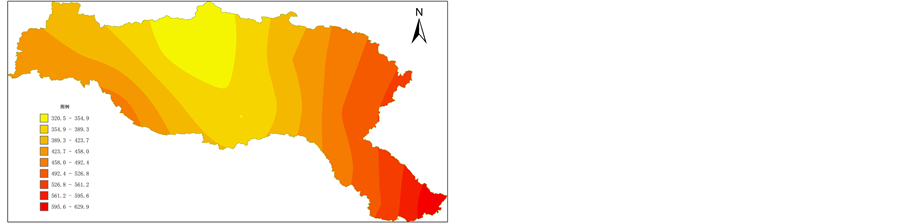
 (a) 20年一遇月降雨量(单位:mm) (b) 50年一遇月降雨量(单位:mm)
(a) 20年一遇月降雨量(单位:mm) (b) 50年一遇月降雨量(单位:mm)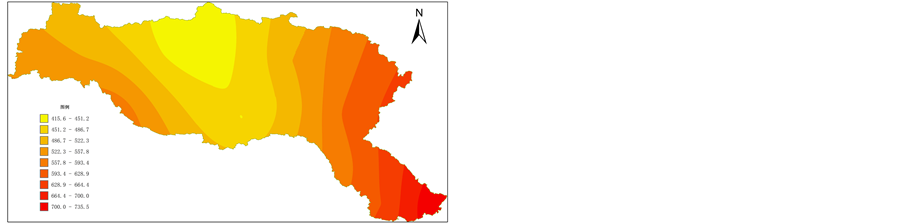
 (c) 100年一遇月降雨量(单位:mm) (d) 200年一遇月降雨量(单位:mm)
(c) 100年一遇月降雨量(单位:mm) (d) 200年一遇月降雨量(单位:mm)
Figure 6. Spatial distribution of monthly rainfall extremes for different return periods in Han River basin
图6. 汉江流域不同重现期月降雨量空间分布图
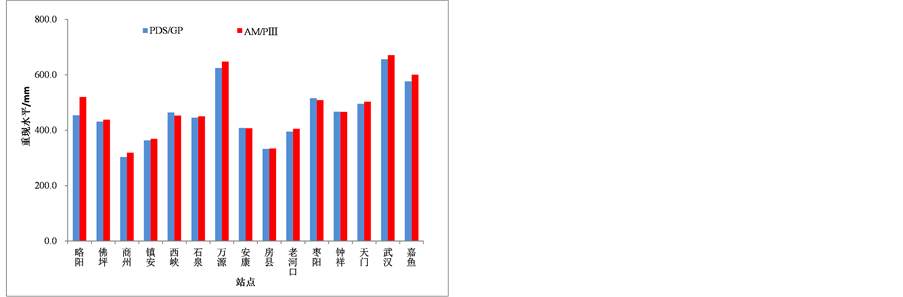
 (a) 20年 (b) 50年
(a) 20年 (b) 50年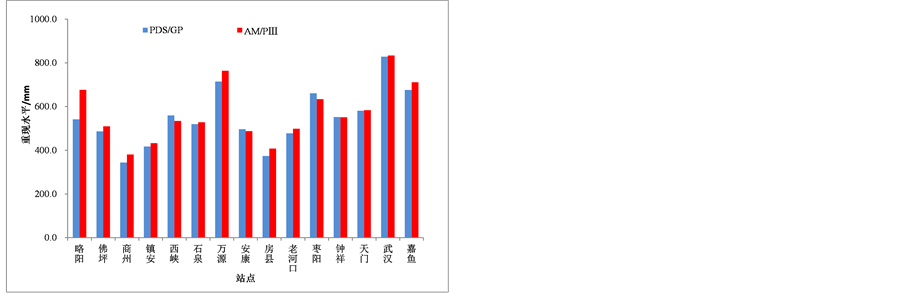
 (c) 100年 (d) 200年
(c) 100年 (d) 200年
Figure 7. Results and comparison between PDS/GP model and AM/PIII model in Han River basin
图7. 汉江流域各站PDS/GP模型和AM/PIII模型计算结果对比图
适的极值模型估计降雨极值重现水平优于传统的频率分析模型。
(2) PDS/GP模型采用了超定量样本,较常规的年最大值系列样本数多,能更充分地利用数据中的极值信息。将PDS/GP模型计算的不同重现期月降雨量与年最大值系列拟合PIII型曲线所得的结果对比分析,前者的估计值受样本最大值影响相对较小,预测结果普遍小于后者。
(3) 要建立合理的PDS/GP模型,很重要的一步是阈值确定,本文将平均超出量函数和参数估计量变化两种阈值确定方法结合使用,大大缩小了可能合理阈值范围,能在一定程度上减少计算工作量;同时采用拟合残差法减小阈值选取的不确定性。
(4) 汉江流域20年、50年、100年和200年一遇的月降雨极值分别为403.3 mm、462.4 mm、506.0 mm和548.8 mm。15个站点中,除了略阳和房县,其它站点的月降雨量极大值50年一遇的95%置信区间都包含了50年实测资料系列的最大值,PDS/GP模型拟合度较高。