1. 引言
随着技术的进步，智能车应用系统的开发也越来越受到重视。它不仅能够提供智能车行驶过程中的各种状态指标，而且能够利用车载设备所获得的各种信息实现对整车的智能控制，减少人为因素的影响，并给驾驶带来方便。在智能车的应用系统中，由车载设备所拍摄的图像占据着重要的地位。图像不仅能够提供感官的直觉信息，而且能够被利用来实现对整车的智能控制。系统在利用图像时，一个基本的要求是高质量的清晰图像，以保证图像所提供的信息的完整性和准确性。然而，由于成像设备的硬件问题，以及在图像的成像、传输等环节出现的图像失真问题，不可避免的会造成获取图像出现模糊等问题。为了去除图像中的模糊问题，很多研究学者和研究机构提出了多种去模糊的方法。
图像去模糊的目的就是根据图像的获取模型从模糊的图像复原得到原始的清晰图像。显然，从模糊图像复原得到清晰的图像是一个逆过程。由于图像的模糊退化函数本身的不可逆性，这就导致了图像的去模糊过程就是一个病态的过程。所以，在图像的去模糊过程中，就需要在这些方法中引入合适的图像正则化约束，从而使得图像的复原尽可能的实现。但是，构造的不同的正则化的约束，在求解的过程中会使得图像的复原效果明显的有差别，因此，基于正则化方法的一个主要研究领域就是构造合适的正则化约束项。除此之外，针对正则化方法的研究，还集中在对模型的最优化求解和正则化参数的选择上[1] 。最具有代表性的正则化的方法就是Tikhonov正则化方法[2] 。这种方法假设清晰的未模糊的原始图像是平滑的，这就使得计算过程简单而有效，但是一个明显的缺点是，所设立的假设条件是单一而理想的，这就使得复原方法所复原的图像在边缘处会出现模糊的情况，对于其他的一些图像还会出现振铃效应和瑕疵[3] 。在传统的Tikhonov模型基础上，Barakat等增加一个关于图像局部信息的约束项，提出了一种改进的Tikhonov正则化图像非盲去模糊方法，从而使得算法获得了更好的复原效果[4] 。Vogel等人在全变差模型的基础上，提出了图像的去模糊方法[5] 。Oliveira等人利用一种上界最小化策略，提出了一种基于全变差的自适应的图像去模糊方法。但是这种方法在处理中心对称的模糊退化函数上有较好的效果，而在其他的情况下，其处理效果并没有那么好[6] 。Beck等在图像梯度的基础上提出了一种梯度约束的全变差的快速图像去模糊方法[7] 。Afonso等提出一种针对不同模糊情况以及计算速度更快的方法[8] 。这种方法在基于全变差模型的图像去模糊方法的基础上，利用变量分裂的约束优化策略来实现图像的去模糊。Li等在Chan等[9] 的基础上，利用分裂布雷格曼迭代策略，提出一种扩展的分裂布雷格曼图像去模糊方法[10] 。在全变差模型的基础上，Gilboa等[11] 提出了图像的非局部全变差模型，并利用此模型来达到图像的去噪处理。在非局部全变差模型提出后，Lou等提出基于这种非局部全变差模型的图像去模糊方法[12] 。Zhang等则提出更有效率的非局部全变差模型的图像去模糊方法[13] 。这种方法利用布雷格曼操作符分裂的最优化迭代策略实现对非局部全变差模型的求解。
虽然非局部全变差模型能够较好地复原出图像的纹理细节，但是在处理图像的边缘成分上时，没有兼顾到图像边缘的影响，这就必将导致复原的图像出现边缘不够锐化等现象。为了解决这个问题，本文提出一种基于非局部全变差模型和全局非零局部秩惩罚的图像去模糊方法。非局部全变差模型主要用于恢复图像中的纹理细节，而非零局部秩惩罚则主要用于约束图像的边缘，达到锐化边缘的目的。实验表明，无论是在模拟模糊图像上，还是在真实的模糊图像上，本文所提出的方法与一些有代表性的方法相比都能达到较好的复原效果。
2. 基于非局部全变差模型的图像去模糊
2.1. 非局部全变差模型
图像的非局部全变差模型是一个用于图像去噪的经典模型。对于一幅大小为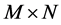
的图像I，那么图像I的非局部全变差模型被定义为[12] ：
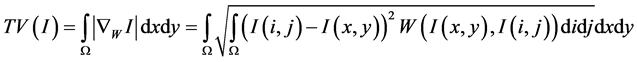(1)
式中，此公式是定义在有界域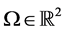
上的一个去噪模型，x，y，i，j表示图像中像素点的坐标，
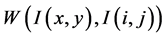是图像中非局部权值，这种非局部的权值计算公式为：
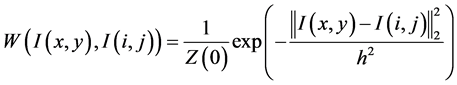(2)
式中：
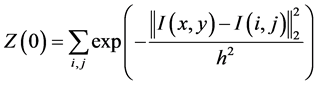(3)
式中，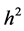
为滤波参数。
2.2. 基于非局部全变差模型的图像去模糊
基于非局部全变差模型的模糊图像复原方法主要是将图像的模糊退化模型与图像的非局部全变差模型相结合，实现去模糊的效果。假设一幅模糊降质图像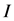
，则基于非局部全变差模型的模糊图像复原方法的数学模型为：
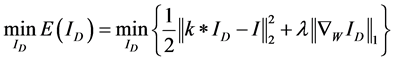(4)
式中，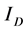
表示复原的图像，
表示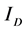
的正则化参数，
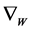表示非局部的梯度算子，
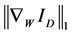为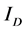
的离散形式的非局部全变差模型，即：
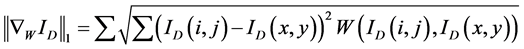(5)
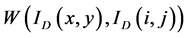为非局部相似性的权值。
由上面的复原公式可以看到，这种方法主要的作用还是在恢复图像的细节纹理上，所以就有一定的局限性。使得边缘部分的复原效果不理想。
3. 局部秩
对于图像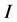
中的某个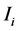像素
，像素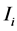
的局部秩定义为在像素
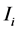的邻域
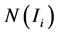内比像素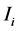
小的像素个数[14] ，即：
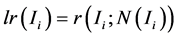(6)
那么整个图像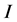
的局部秩变换就表示为：
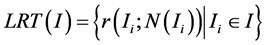(7)
图像的局部秩能够很好的用到图像的边缘提取上。
4. 所提出的方法
4.1. 非零局部秩惩罚约束项
在第三节中已经说明，图像的局部秩能够很好的用到边缘提取上，所以，为了能够在模糊图像复原的过程中，实现对边缘的约束和处理，本文提出图像的非零局部秩惩罚约束。因为图像的局部秩能够体现出图像的边缘，也就意味着，当利用这种边缘特征对图像做边缘约束时，复原图像的边缘将会更锐化。图像的局部秩图像由于其本身的特点，在边缘处，其局部秩是有数值的，但是在非边缘的部分，其数值则表现为零。那么为了实现对边缘的约束，提出如下所示的统计特征：
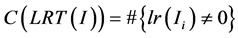(8)
此公式主要统计边缘出现的局部秩信息，则非零局部秩惩罚约束项就表示为：
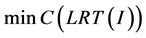(9)
通过这样的惩罚，就可以实现对边缘的约束。
4.2. 基于非局部全变差和非零局部秩惩罚的去模糊模型
传统的基于非局部全变差模型的去模糊方法，虽然能够使得复原的图像的细节和纹理部分更丰富和清晰，但是，这种复原方法没有考虑到图像边缘成分的影响，必然导致重建的结果边缘不够锐化，而且会存在一些瑕疵。为了能实现在复原的过程中对边缘进行约束，达到锐化边缘的目的，本文提出一种基于非局部全变差和非零局部秩惩罚的去模糊模型，这种去模糊的模型表示为：
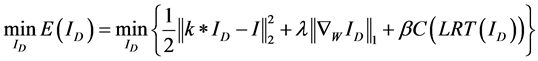(10)
从这个公式中，可以明显的看到，第一项主要用来约束图像的复原过程与图像的观测模型相一致，中间的一个项用来实现图像纹理细节的复原，而最后一项的惩罚项，则主要用来实现对边缘的约束。这样，所提出的模型不仅能够复原较多的纹理和细节，而且能锐化复原图像的边缘。
5. 实验验证分析
5.1. 实验设置
所有的实验都是在CPU为2.80 GHz和2.90 GB内存的台式电脑上实现。如图1所示为本次实验中所用到的模拟模糊图像和真实的模糊图像。模拟模糊图像被加入了噪声水平为0.002的高斯白噪声。实验对比的算法主要有文献[13] 的方法。
5.2. 实验结果
为了测试本文所提方法的效果，将本文的方法分别利用到模拟模糊图像和真实模糊图像的复原上。图2显示了在不同方法下，对模拟图像的去模糊效果。在图中，右下角为对应的模糊核。从图1中可以明显的看到，文献[13] 的方法虽然能够较好的复原出图像，但是，在边缘处和图像的其他地方，有较多的瑕疵，而且边缘处也有较大的振铃效应。本文所提出的方法，不仅能够较好复原出清晰的图像，而且所复原的图像，其边缘更锐化，瑕疵更少。
图3显示了在不同方法下，对真实模糊图像的去模糊效果，黑色部分为图像的模糊核。为了展示不
同算法的视觉效果，将复原结果的一部分局部放大图也显示出来。从图3中可以看到，文献[13] 的方法能够复原出较为清晰的图像，但是在一些细节处和图像的边缘处出现明显的不清晰和瑕疵，而且重建图像的边缘也不够锐化。与此相比，本文所提的方法，所复原的图像更加清晰，细节更丰富，而且边缘也更锐化。
上述的两个实验说明，本文所提的方法不仅能较好的复原模糊图像，而且所复原的图像更清晰，细
Figure 1. Test images. Left is real clean image and right is real blur image
图1. 测试图像。左边为真实清晰图像，右边为真实模糊图像
(a) (b) (c)
Figure 2. Recovery results of analog image: (a) Blur image; (b) Result of [13] ; (c) The proposed method
图2. 模拟图像复原效果：(a) 模拟模糊图像；(b) 文献[13] 的方法；(c) 本文方法
(a) (b) (c)
Figure 3. Recovery result of real blur image: (a) Real blur image; (b) Result of [13] ; (c) The proposed method
图3. 真实模糊图像的复原效果：(a) 真实模糊图像；(b) 文献[13] 方法；(c) 本文方法
节也更锐化，这是因为，本文的方法不仅利用了图像的非局部特征，而且引入了图像的边缘约束特征，使得复原效果更佳。
4. 结论
本文面向未来汽车功能模块发展趋势，针对图像模糊问题，在传统的基于非局部全变差图像去模糊模型的基础上，提出一种基于非局部全变差模型和非零局部秩惩罚的模糊图像复原方法。非局部全变差模型主要是为了实现纹理细节的复原，而非零局部秩惩罚则主要是为了锐化复原图像的边缘。实验结果表明，所提的方法不仅能够较好的复原模拟模糊图像，而且对真实的模糊图像也有较好的复原效果。
基金项目
重庆市应用开发计划项目(cstc2013yykfC60006)，重庆市应用开发计划项目(cstc2013yykfB60006)。