1. 引言
在计算流体力学(CFD)应用中，采用混合网格方法不但对复杂构型具有强大的几何适应能力，网格生成的人工工作量少，而且易于通过采用不同的单元类型及调整网格的疏密来适应不同的流场特征，并容易生成整体网格、整体求解。但是，在实际应用中，混合网格方法也遇到了一些困难，比如对于多体相对运动问题，就需要对网格进行再生，处理非常复杂。
为了解决这一问题，Nakahashi [1] 首先提出了非结构网格重叠方法。该方法吸收了结构网格重叠方法[2] 的优点，后来又被推广到混合网格重叠及动态重叠应用中[3] -[6] ，得到了较大的发展。尽管如此，混合网格重叠方法目前仍然面临诸多难题，其中，网格间边界的定义及其插值方法就是其中一个重要方面。已有研究均基于多层网格节点的流场变量进行插值计算，该思路实现较为繁琐，且容易在高速流动强间断附近产生较大的耗散。
本文在优化网格间边界定义的基础上，给出一种适用于任意单元类型的插值策略。该方法应用简洁方便且能够保证二阶空间的离散精度，非常适用于亚跨超全速域流场的数值计算。
2. 数值方法
本文算法构造基于任意多面体混合网格单元。算法不考虑具体的网格拓扑，对不同的单元类型统一处理。空间离散采用格心有限体积法，控制体取网格单元，控制面取单元表面，流场变量存储在单元中心。
2.1. 控制方程
舍去源项的三维非定常可压缩NS方程组在直角坐标系下的守恒积分形式可表示为
(1)
式中：
为控制体；
为控制面；
为守恒变矢量；
为对流通量；
为粘性通量。各项的具体描述详见文献[7] 。
2.2. 数值离散方法
对流通量离散采用Roe [8] 格式近似求解Riemann问题。假设控制面
的左右单元分别为
和
,则对流通量可表示为
(2)
式中：
为Roe平均矩阵；
和
分别为控制面的左右状态。如果
和
分别取左右单元中心的平均值，则空间离散只有一阶精度，为了达到二阶精度，就需要对其进行重构。
Barth [9] 提出的线性重构方法假定解在控制体内呈线性分布，面左右两侧的值可表示为
(3)
式中：
为任意流场变量值；
为单元
体心的梯度；
为限制器函数；
为从体心到面心的矢量。
采用最小二乘法[7] 计算，
采用收敛特性非常好的Venkatakrishnan [10] 限制器。
另外，粘性通量采用中心格式离散，湍流模型采用Spalart-Allmaras [11] -方程模型，时间离散采用LU-SGS格式[7] 。
3. 混合网格重叠方法
与现存的基于格点[3] -[6] 的混合网格重叠方法不同，本文基于格心展开，通过网格间边界定义后，初始网格单元被分为三类：活动单元、插值单元和非活动单元。活动单元在计算区域内部参与流场计算，插值单元分布在网格边界用于子网格间的信息交换，非活动单元作为非计算单元被挖去。另外，本文定义包围插值单元网格中心点的单元为其宿主单元。图1给出了一个网格边界定义示例。其中，子网格G2中单元B(1-2-3)是子网格G1中单元A(a-b-c)的宿主单元，这是因为单元A的格心落在了单元B的内部。
3.1. 插值方法
在本文混合网格重叠系统的流场计算中，子网格间的信息交换需要插值单元通过其宿主单元来获取其它子网格的相应边界信息，这一信息交换过程称为插值。与传统的完全依赖于格点流场变量进行插值的方法不同，下面给出一种新型的插值策略。
该方法依赖于插值单元的格心流场变量值、单元梯度值和限制器函数值的计算来完成。比如图1，
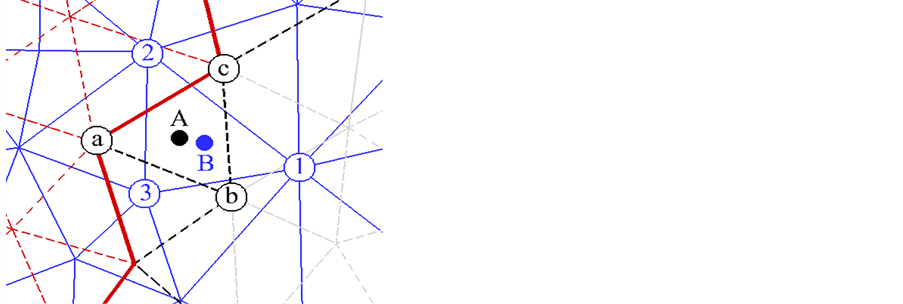
Figure 1. Intergrid-boundary definition between two subgrids: G1 and G2 图 1. 两子网格间边界定义示例
插值单元A的状态可以通过下式确定
(4)
通过上式计算，插值单元A可以充分利用宿主单元B的所有相邻单元的信息。这是因为式(4)与式(3)相类似，
和
都是通过单元B的所有相邻单元构造得来。显然，这里要求宿主单元B在流场重构时能够构造出足够多的模板。
当网格间边界重叠区附近流动梯度变化较小时，该插值方法与线性重构一样，可使空间离散精度达到二阶。当边界附近流动变化剧烈时，也可以通过调整重叠区网格的分辨率来提高插值精度，并且这时满足插值单元与其宿主单元的尺寸匹配尤为重要。
因此，上述插值方法应用简洁方便并且能够保证计算精度。它只需要一层插值单元，就可以充分利用其宿主及所有相邻单元的信息。并且，因为借助了上一时间步已经确定的梯度值，所以同梯度计算方法一样，该插值方法适用于任意网格单元类型间的插值计算。
另外，应用本文插值方法，插值边界可以同其它边界条件一样，在复杂求解器中可以做到透明处理。即迭代计算中，插值单元与其它边界虚网格单元功能类似。
3.2. 网格间边界定义方法
本文中网格间边界定义过程可归纳为两步：网格分类和边界优化。首先通过以物面距离作为网格分类参数，将网格单元分为活动单元和非活动单元，形成初始分类边界。然后在初始分类的基础上，对边界进行优化，将网格单元分为活动单元、插值单元和非活动单元，最终形成插值边界。边界优化过程主要考虑如下几点因素：
1) 保证插值单元必须存在宿主单元。因为插值单元的流场信息是从它在其它网格的宿主单元获得的，所以只有保证存在宿主单元，流场计算才能正确进行。
2) 保证插值单元只存在一个宿主单元。因为实际应用中可能是任意多个子网格的任意单元类型重叠在一起，所以对一给定插值单元可能存在多个宿主单元。
3) 清除孤点。所谓孤点就是与周围单元的类别不相同的局部小部分网格单元，它可能是活动单元，也可能是非活动单元。在流场计算中，孤点的存在不但会损害计算精度而且还会降低收敛效率。
4) 适当把插值边界外移，即保证适当的重叠区域，以保证流场计算中宿主单元重构时足够的模板需求，从而有利于提高流场重构精度。
5) 光滑插值边界，且尽量保持插值单元和宿主单元的网格尺寸一致，从而有利于提高插值精度。
图2给出了五球体不同单元类型的边界定义结果。可见，本文方法定义的网格间边界光滑，网格尺寸大小匹配，网格重叠区域大小适当，说明本文给出的网格间边界定义方法是优秀可靠的。
4. 算例验证
4.1. 三段翼(亚声速)
本节选取三段翼亚声速绕流算例来测试上述插值方法的计算精度。来流马赫数取为0.2，雷诺数为
，攻角为10˚。具体实验模型和实验数据详见文献[12] ，另外，文献[13] 中也给出了一个数值计算结果。图3是单区计算网格。图4给出了多区重叠计算装配后的网格，包括分别绕前缘缝翼、主翼和襟翼的三个子网格。从图4可见，网格装配后的插值边界十分光滑，且重叠区附近网格尺寸匹配性很好。
Figure 2. Examples of intergrid-boundary definition of a five-sphere set 图 2. 五球体重叠网格边界定义示例
Figure 3. Single grid over 3-element airfoil 图 3. 三段翼单区计算网格
图5给出了等马赫线的计算结果对比，可见单区计算与多区重叠计算的结果十分一致，且重叠区附近的等值线非常光滑。图6对比了压力分布，发现数值计算结果与实验结果非常吻合，且两个数值计算结果的差别十分小。本算例说明本文发展的插值方法在亚声速计算中是准确可靠的。
4.2. RAE2822翼型(跨声速)
本节选取RAE2822翼型跨声速绕流算例进行测试。来流马赫数取为0.75，雷诺数为
，攻角为2.81˚。具体实验模型和实验数据详见文献[13] 。
同样分别采用单区网格和多区重叠网格进行计算。图7(a)给出了单区计算网格，其中壁面附近采用四边形，其它外围区域采用三角形填充。图7(b)给出了多区重叠计算装配后的网格，包括背景网格和绕
Figure 4. Overset grid over 3-element airfoil. 图 4. 三段翼多区重叠计算网格
(a) (b)
Figure 5. Comparison of Mach contours of 3-element airfoil. (a) Result of single grid; (b) Result of overset grid 图5. 三段翼等马赫线图对比。(a)单区计算结果；(b) 重叠计算结果
翼型的子网格，其中绕翼型的子网格的网格分布与单区计算网格完全一致。
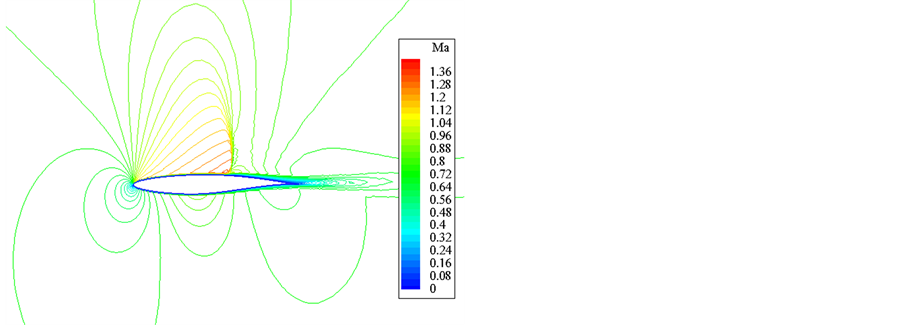
图8给出了等马赫线的计算结果对比，可见单区计算与多区重叠计算的流场结构几乎完全一致，且穿越重叠区的等值线过度光滑。图9对比了压力分布，可见数值计算结果与实验结果非常吻合，且两个数值计算结果的差别非常小。本算例说明本文发展的插值方法在跨声速计算中能够准确捕捉激波位置。
4.3. 轴对称压缩拐角(超/高超声速)
本节选取轴对称压缩拐角算例来测试本文方法对于超/高超声速流动的计算精度。计算模型详见参考文献[14] ，来流马赫数取为5，以前段圆柱长为特征长度，雷诺数取为
，壁面为等温壁，取值为290 K。由于本算例存在大分离区和强激波，所以对于考察算法的间断捕捉能力十分有效。
图10分别给出了单区计算网格和多区重叠计算网格。多区重叠计算网格的疏密分布和网格总量与单区计算网格基本一致。为考验算法的可靠性，单区网格的不同单元接触面以及多区网格的重叠区均取在分离区边缘附近，且穿越所有激波结构。
图11等马赫线的计算结果对比，可见单区计算与多区重叠计算的流场结构相同，且前缘激波、分离激波、再附激波、分离区和膨胀扇区的位置都十分一致。并且，从放大图11(c)中可以看出分离强激波在
Figure 7. Computational grid over RAE2822. (a) Single grid; (b) Overset grid 图 7. RAE2822翼型计算网格。(a)单区网格；(b)重叠网格
穿越重叠区时能够光滑过度，说明本文发展的插值方法能够在不同单元类型子网格重叠时准确捕捉强间断。
图12对比了计算的摩擦阻力系数分布，从图可见多区重叠计算的分离位置和再附位置分别在X/L =
(a) (b)
Figure 8. Comparison of Mach contours of RAE2822 airfoil. (a) Result of single grid; (b) Result of overset grid 图 8. RAE2822翼型等马赫线图对比。(a)单区网格结果；(b)重叠网格结果
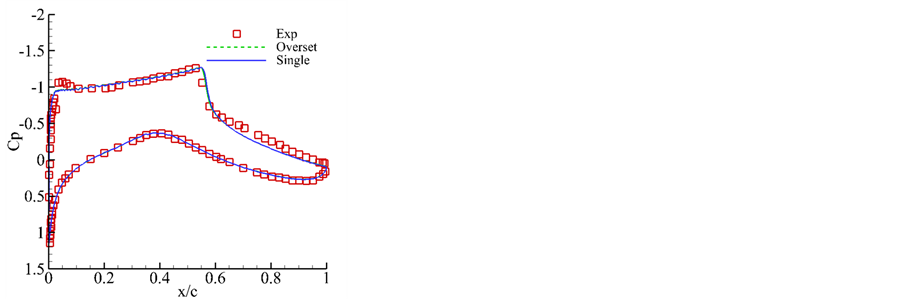
Figure 9. Comparison of pressure coefficient of RAE2822 图 9. RAE2822翼型壁面压力分布对比
(a) (b)
Figure 10. Computational grid over symmetric compress corner. (a) Single grid; (b) Overset grid 图10. 轴对称压缩拐角计算网格。(a)单区网格；(b)重叠网格
0.68和X/L = 1.22附近，单区计算比多区重叠计算的分离区略大一点。文献[14] 中给出实验分离位置和再附位置分别为X/L = 0.7和X/L = 1.15，说明两个数值计算对分离区的预测结果是可靠的。
(a)
(b) (c)
Figure 11. Comparison of Mach contours of symmetric compress corner. (a) Single grid; (b) Overset grid; (c) Amplificatory show of overset grid simulation 图 11. 对称压缩拐角等马赫线图对比。(a)单区网格；(b)重叠网格；(c)重叠计算结果局部放大图
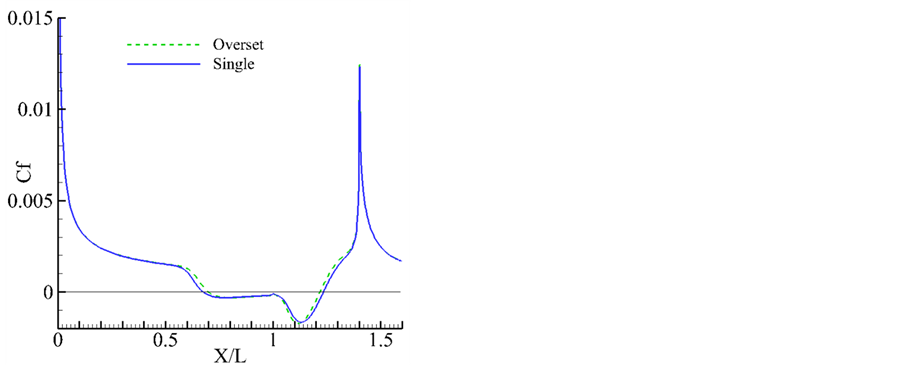
Figure 12. Comparison of resistance coefficient of axisymmetric compress corner. 图 12. 轴对称压缩拐角摩擦阻力系数分布对比
5. 结论
1) 本文插值方法依赖于插值单元的格心流场变量值、单元梯度值和限制器函数值的计算来完成，只需要一层插值单元，就可以充分利用其宿主及所有相邻单元的信息。
2) 本文给出的网格间边界定义方法是优秀可靠的，所定义的网格间边界光滑，网格尺寸大小匹配，网格重叠区域大小适当。
3) 通过亚声速三段翼、跨声速RAE2822翼型和超/高超声速轴对称压缩拐角算例验证表明，单区计算与多区重叠计算结果差别非常小，且均与实验结果吻合较好，说明本文方法适用于亚跨超全速域流场的数值模拟。