1. 引言
压电材料不仅具有正、逆压电效应，并且具有频响范围宽、比重小、成本低、技术成熟、应用方便等优点，目前，已被广泛应用于航空航天、机械制造、交通运输和土木建筑等领域，且其应用领域仍在不断扩大，但压电材料在制造或使用过程中不可避免地存在脱层损伤缺陷，这将对结构的动力学特性产生一定的影响。另外，压电结构常使用在航空航天领域，经常处于恶劣的湿热环境中，温度和湿度的增加会引起严重的湿热残余应变和残余应力,使得结构的动力学特性发生改变，因此湿热环境成为不可忽略的影响因素。
为此，人们对考虑湿热效应的具脱层压电结构的非线性动力学行为予以密切地关注，但由于该问题的研究涉及湿热效应，压电效应，脱层损伤，几何非线性，且分析当中还需考虑脱层间的接触效应，这样势必使问题的建模和求解十分复杂。所以，现有的研究成果中，大多是关于复合材料脱层梁板振动方面的研究。Ramazan-Ali Jafari-Talookolaei [1] 研究了具脱层旋转复合材料梁自由振动的解析解。D. Garcia [2] 等在自由振动复合材料层合板中进行了脱层损伤探测方面的研究。Yin W.L.和Jane K.C. [3] 研究了屈曲状态下具对称脱层梁–板的振动，给出了轴力和脱层长度对梁固有频率的影响。Chang T.P.和Ling J.Y. [4] 研究了后屈曲状态下对称脱层梁–板的振动问题，给出了不同轴力和不同脱层长度下结构的固有频率。Luo H.和Hanagud S. [5] 以及Wang J.和Tong L. [6] 考虑了脱层区的接触效应，在脱层区引入假想弹簧，对脱层梁的动力问题进行了探讨。考虑剪切变形及转动惯量，Mohammad H. [7] 等给出了一种新的脱层层合梁自由振动问题的半解析解，探讨了各种参数对脱层梁动力响应的影响。A. Rama Mohan Rao [8] 等提出了一种用于复合材料层合结构中脱层检测的新技术。Chattopadhyay和Radu [9] [10] 运用高阶剪切变形理论并采用有限元方法，分析了复合材料脱层板在动载荷作用下的动力稳定问题。Yang和Dong [11] 采用Timoshenko梁理论及脱层振动问题中“自由”、“限制”两种模型分析了多处脱层旋转梁的自由振动。Y. Liu和D.W. Shu [12] 欧拉–伯努利梁理论首次分析了具单一脱层功能梯度梁的自由振动。至于对湿热条件下具脱层压电结构非线性动力问题的研究还鲜见报道。
本文考虑脱层区的接触影响，分析了湿热条件下具脱层压电梁的非线性动力响应问题。在求解中，空间上采用差分法离散，时间上采用Newton-Newmark方法离散，整个问题采用迭代法进行求解。算例中，详细讨论了电压、温度、湿度、脱层的长度、深度及外载荷幅值等因素对具脱层压电梁非线性动力响应的影响。
2. 基本控制方程
考虑图1所示的含贯穿脱层的压电梁，其长度和高度分别为L和h，质量密度为
。脱层将梁分为四部分，分别记为
。每部分的x坐标原点取在各部分的最左端。 各部分子 壳的长度分别为L1、L2、L3和 L4 (L2 = L3)，子壳2的厚度为h2，子壳3的厚度为h3，且h2 + h3 = h。
设
分别为脱层压电梁内任一点在x和z方向的位移，它们在中面上的值分别为
，则压电梁的位移分量可表示为：
(1)
其中，下标(，)表示对坐标变量求偏导。
压电梁内任一点非线性应变–位移关系可表示为
(2)
且
(3)
对考虑湿热效应的压电梁而言，其本构关系为
(4)
上式中，
,
及
分别代表湿热系数以及电场强度，
，
分别为材料的弹性常数及压电常数。
且
(5)
上式中，
，
为压电材料的材料常数，
为压电应变常数。
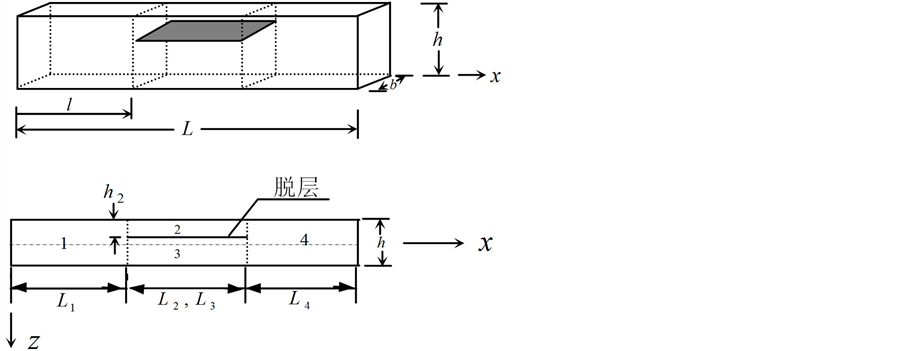
Figure 1. Geometry of piezoelectric beam with delamination
图1. 脱层压电梁几何示意图
若电场仅有沿梁厚度方向的分量
，则电场强度
和外部所加电压
之间的关系如下：
(6)
设脱层压电梁各部分承受的横向载荷为
，忽略体力和面内惯性力的影响，则由最小势能原理可得其非线性运动控制方程为
(7)
上式中，
为接触效应系数，且有
。
为子壳2、3之间沿垂直于x方向每单位长度的接触力，且
应当满足如下的条件：
(8)
为简化问题，可选取式(8)中的函数
为线弹簧函数，即
(9)
在式(9)中，弹性系数k的值待确定。而且，由于预先无法知道w2，w3的值，即判断不出
还是
，故式(8)中的接触力
也待确定。
首先，确定k值。k值可以用两串联弹簧的等效弹性系数来近似，将脱层的上下两部分，即2区和3区分别视为一个弹簧，当脱层面接触时，其中一部分，例如2区将承受力
，于是2区在力
作用下，其接触处的厚度改变量为
(10)
同样，力
也作用于3区，则相应有
(11)
因此，2、3区中面的相对位移为
(12)
将式(10)、(11)代入式(12)后，再与式(9)联立求解，可得
(13)
然后，确定
。注意到不管
取何值，式(8)等价于
(14)
其中
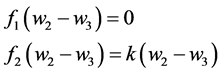
式(14)又可与下列表达式近似等价
(15)
其中
是
和
的函数，且满足如下的条件：
(16)
满足上述条件的函数
可取为
(17)
其中A为某一给定的大数，它可根据问题所要求的精度来取值(算例中取A=1015)。因此，当
时，接触力
可近似地表示为
(18)
将
代入上式，得
(19)
式(19)即为脱层间接触力的计算式。
利用压电梁的几何、本构关系及式(7)，并引入如下无量纲参数
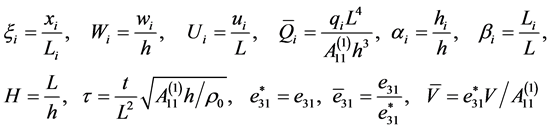
可得湿热条件下用位移表示的脱层压电梁的无量纲非线性运动控制方程为
(20)
上式中，
.
假定梁两端的支承为夹支可动，则其无量纲边界条件、位移和力的连续条件分别为
无量纲边界条件：
(21)
无量纲位移连续条件：
(22)
无量纲力连接条件：
(23)
其中：
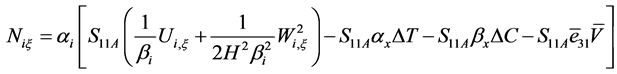
圆柱壳的初始条件为：
(24)
3. 求解方法
为了寻求满足初始条件(24)、边界条件(21)、位移连续条件(22)以及力连接条件(23)的非线性运动微分方程组(20)的解，我们将无量纲位移函数
在空间和时域内离散，以求其近似解。
在空间上采用差分法离散。对于线性项的处理，型如
等各阶偏导数项，以
为例采用差分格式，有
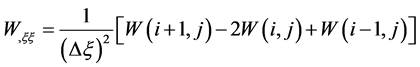
对照差分格式，可以容易的求得控制方程中其余各线性项的各阶偏导数的差分表达式。
在时间上将外载荷的作用时间
等分为
等份，记每一等份为
，整个问题采用迭代法求解。在任一迭代步
中，控制方程(20)和定解条件(21)~(23)中的非线性项被线性化，且写为如下的形式[13]
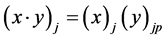
式中
是前二次的迭代值的均值。对于初始迭代步，可以应用二次外推法求解，即
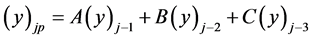
对于不同的迭代步，系数
可以分别取如下的数值
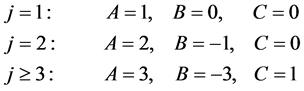
对于三次非线性项的处理方法与二次非线性项的处理方法相同，经过线性化处理以后，最后保留一次线性。
然后，应用平均加速度法，方程组(20)中的加速度可表示为
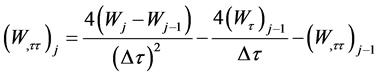
其中：
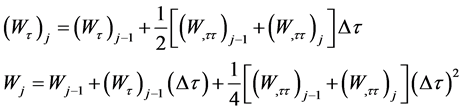
经过差分处理和线性化以后，控制方程和定解条件由最初的偏微分方程组转化为差分格式的线性代数方程组。联立求解方程组，对每一时间步采用迭代法求解，迭代过程持续到相邻两次所得计算结果的误差小于0.1%，在第
步取得收敛解后，该迭代步终止，再进行第
步的计算。
4. 计算结果
考虑一由压电陶瓷PZT-5构成的具脱层压电梁，其材料参数为
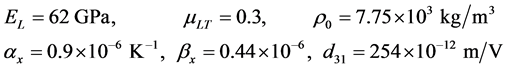
脱层压电梁壳的几何参数为
，横向外载荷
，本文算例中
，
，外激励频率
。图中纵坐标为脱层2、3区中点的无量纲挠度
，横坐标为无量纲时间
。
图2给出了几何非线性对脱层压电壳2、3区中点非线性时程响应曲线的影响。压电梁脱层参数为
，外载荷幅值
，电压
，湿热条件
，
。通过比较可以看出，几何线性和几何非线性的解相差非常显著。线性解高估了脱层压电梁的振动幅值，从而低估了结构的刚度。可见，考虑梁的几何非线性因素是很有必要的。
图3给出了电压对脱层压电梁2、3区中点非线性时程响应曲线的影响，压电梁脱层参数、外载荷幅值及湿热条件与图2中的相同。从图中可以看出，负的控制电压会使压电梁内2、3区中点的振动幅值减小，而正的控制电压使压电梁2、3区中点的振动幅值增加。
图4为湿热条件对脱层压电梁2、3区中点非线性时程响应曲线的影响。压电梁脱层参数、外载荷幅值及电压与图2中的相同。从图中可以看出，随着温度和湿度的增加，压电梁振动幅值增大。
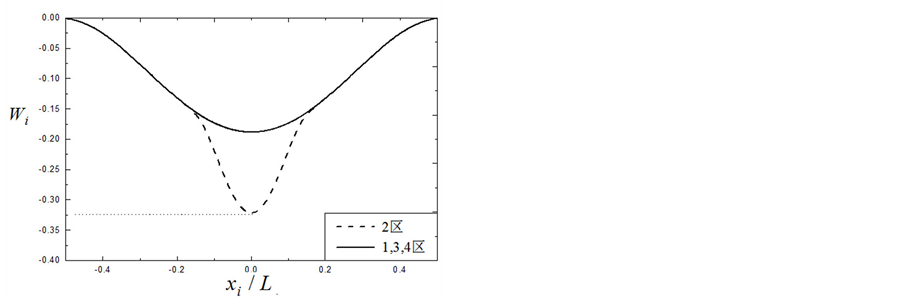
图5给出了当脱层梁2区中点的振动幅值
达到最大值的瞬时，同一时刻脱层梁沿轴向(x方向)其上各点的幅值
。从图中可以看出，在外激励作用下，脱层压电梁发生了较大的局部振动，即2区在振动过程中达到的幅值明显大于其它各区。此外，比较图(5a)与图5(b)可知，当脱层位置固定时，脱层压电梁承受的外载荷幅值越大，其在振动过程中达到的幅值也越大。比较图(5a)与图5(c)可知，当脱层深度
和外载荷幅值Q相同时，脱层的尺寸越大，其在振动过程中达到的幅值也越大。比较图(5a)与图5(d)可知，当脱层长度
和外载荷幅值Q相同时，脱层越靠近梁外表面，其在振动过程中达到的幅值越大。
Figure 2. Effect of geometric nonlinear on the time-displacement curves of piezoelectric beam with delamination
图2. 几何非线性对脱层压电梁时程响应曲线的影响
(a) 负电压影响 (b) 正电压影响
Figure 3. Effect of voltage on the nonlinear time-displacement curves of piezoelectric beam with delamination
图3. 电压对脱层压电梁非线性时程响应曲线的影响
(a) ΔT = 0, ΔC = 0 (b) ΔT = 300, ΔC = 0.03
Figure 4. Effect of hygrothermal condition on the nonlinear time-displacement curves of piezoelectric beam with delamination
图4. 湿热对脱层压电梁非线性时程响应曲线的影响
(a) α2 = 0.2, β2 = 0.3, Q = 100 (b) α2 = 0.2, β2 = 0.3, Q = 80
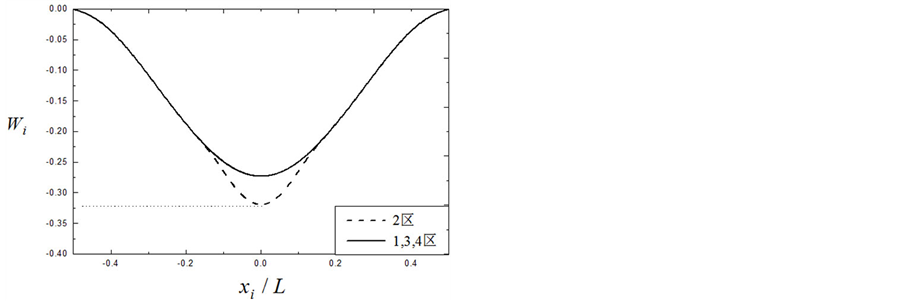
(c) α2 = 0.2, β2 = 0.2, Q = 100 (d) α2 = 0.3, β2 = 0.3, Q = 100
Figure 5. Deflection of each point along x of piezoelectric beam with delamination
图5. 脱层压电梁沿轴向各点的响应幅值
5. 结论
本文基于压电理论及非线性梁理论，建立了考虑湿热及接触效应的具脱层压电梁的运动控制方程。通过引入假想弹簧所算得的接触力对系统的横向振动控制方程进行修正，从而有效地避免了脱层之间的相互贯穿。算例中，讨论了电压、温度、湿度、脱层的长度、深度及外载荷幅值等因素对具脱层压电梁非线性动力响应的影响。主要结论如下：
(1) 几何线性高估了结构的振动幅值，进而低估了结构的刚度。
(2) 正的控制电压可使脱层压电梁的振动幅值增大，而负的控制电压可使脱层压电梁的振动幅值减小。
随着温度和湿度的增加，压电梁振动幅值增大。
(3) 当脱层越长、越靠近梁外表面以及横向外载荷越大时，脱层压电梁在振动过程中达到的幅值也越大。
基金项目
国家自然科学基金资助项目(No: 11102028)。