1. 引言
自发现孤立波以来,求解非线性偏微分方程的方法层出不穷。传统的方法有:Bäcklund变换[1] 、Hirota双线性变换法[2] 、Darboux变换法[3] 、Painlevé展开法[4] 等。随着计算机技术的发展,结合非线性科学和机械化数学的深入研究,人们又发现了很多求解非线性发展方程的新方法:Jacobi椭圆方程展开法[5] 、齐次平衡法[6] 、Riccati方程展开法[7] 、辅助方程法[8] 、Wronsk形式展开法[9] 、 -展开法[10] 等。前面提到的求解非线性偏微分方程的方法中:Jacobi椭圆函数展开法、齐次平衡法、Riccati函数法、
-展开法[10] 等。前面提到的求解非线性偏微分方程的方法中:Jacobi椭圆函数展开法、齐次平衡法、Riccati函数法、 -展开法都可以归类为辅助方程法[11] [12] 。辅助方程法是一种非常直接也有效的求解方程的方法。求解非线性偏微分方程,目前没有统一的求解方法,而且获得的精确解通常是单孤子解、双周期解、多孤子解,很少获得同时包含有理函数、双曲函数、三角函数、指数函数、雅克比椭圆函数的相互作用解。
-展开法都可以归类为辅助方程法[11] [12] 。辅助方程法是一种非常直接也有效的求解方程的方法。求解非线性偏微分方程,目前没有统一的求解方法,而且获得的精确解通常是单孤子解、双周期解、多孤子解,很少获得同时包含有理函数、双曲函数、三角函数、指数函数、雅克比椭圆函数的相互作用解。
本文中我们对新辅助方程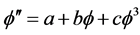 进行四类函数的求解,成功获得了三角函数、双曲函数、指数函数、Jacobi椭圆函数,并将其成功应用于带有扰动项的非线性Schrödinger方程中。
进行四类函数的求解,成功获得了三角函数、双曲函数、指数函数、Jacobi椭圆函数,并将其成功应用于带有扰动项的非线性Schrödinger方程中。
2. 新辅助方程四类函数解
新辅助方程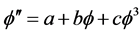 进行解的新的构造:
进行解的新的构造:
情况1: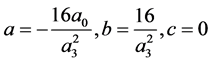
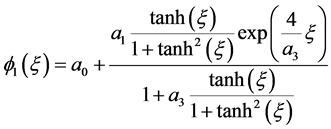
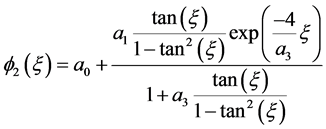 (1)
(1)
情况2: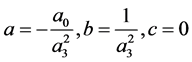

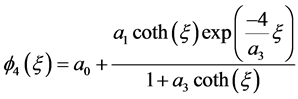
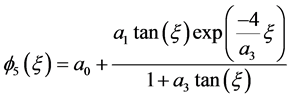 (2)
(2)
情况3: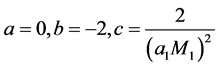
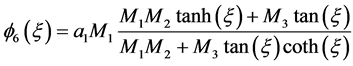
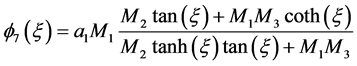
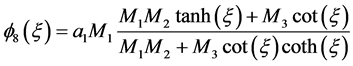

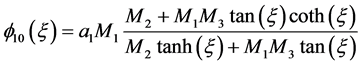
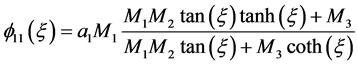
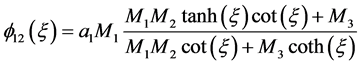
 (3)
(3)
情况4: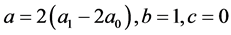
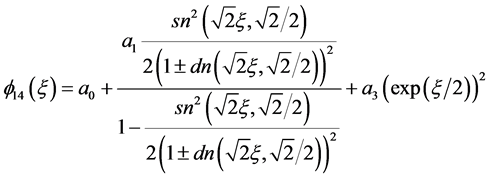
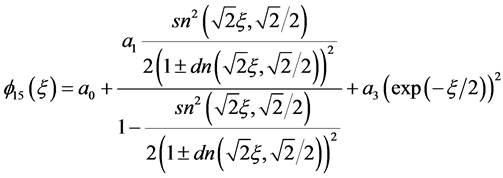 (4)
(4)
其中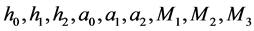 为任意常数。
为任意常数。
新辅助方程方法步骤如下:
第一步:非线性偏微分方程的一般形式:
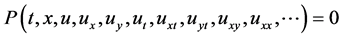 (5)
(5)
第二步:作行波变换:
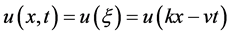 (6)
(6)
其中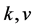 是任意常数。
是任意常数。
第三步:把(6)代入方程(5),得到一个常微分方程:
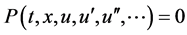 (7)
(7)
第四步:假设方程(5)的精确解有如下形式:
 (8)
(8)
其中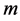 是正整数,可由齐次平衡方程(5)中的最高次项和非线性项确定其值。
是正整数,可由齐次平衡方程(5)中的最高次项和非线性项确定其值。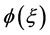 满足新辅助方程。将方程(8)代入方程(7),得到关于
满足新辅助方程。将方程(8)代入方程(7),得到关于 的多项式,合并同类型进行化简使
的多项式,合并同类型进行化简使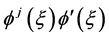 的每项系数为零,得到一系列关于
的每项系数为零,得到一系列关于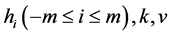 的超定方程组,借助科学工具Maple求解。
的超定方程组,借助科学工具Maple求解。
3. 扰动项的非线性 Schrödinger方程的四类函数解
带有扰动项的非线性Schrödinger方程[13] :
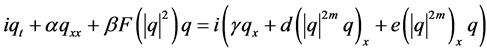 (9)
(9)
该方程作为光脉冲的传播的一个数学模型,可以广泛应用于非线性光学领域中。其中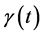 为模型内部的色散系数,
为模型内部的色散系数,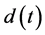 表示短脉冲的自陡峭系数,
表示短脉冲的自陡峭系数,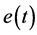 为高阶的色散系数。本文主要考虑带有扰动项方程非线性特征的Kerr律:
为高阶的色散系数。本文主要考虑带有扰动项方程非线性特征的Kerr律:
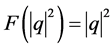 (10)
(10)
根据Kerr律方程(9),不失一般性当 :
:
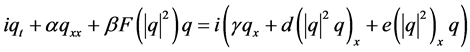 (11)
(11)
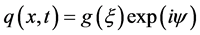 (12)
(12)
其中 ,代入方程(11)使其虚数部分为零,我们得到一个关系式:
,代入方程(11)使其虚数部分为零,我们得到一个关系式:
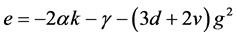
方程(11)简化成:
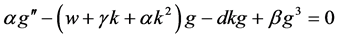 (13)
(13)
应用新辅助方程,求解方程:
1) 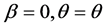
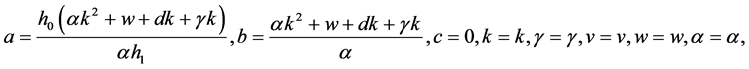
方程(11)的相互作用解:
情况1: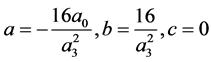
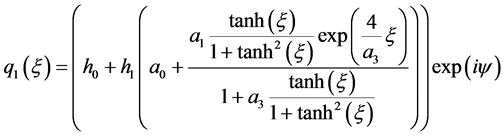
 (14)
(14)
情况2: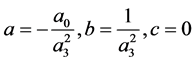
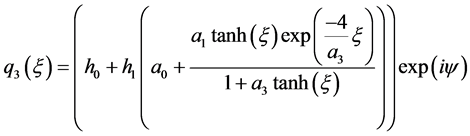
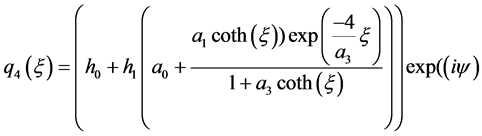
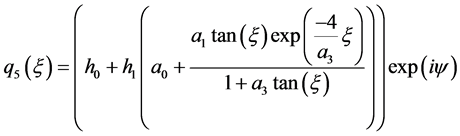 (15)
(15)
情况4: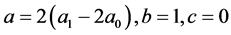
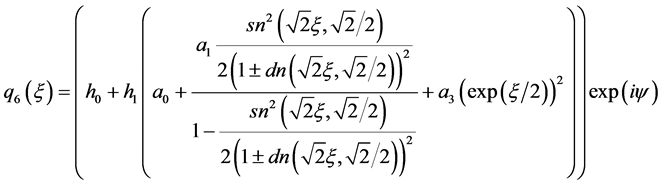
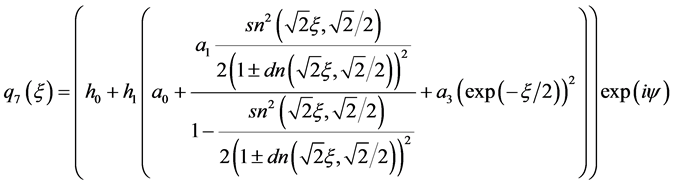 (16)
(16)
2) 当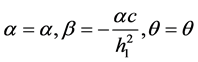
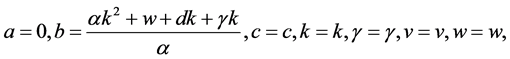
方程(11)的相互作用解:
情况3: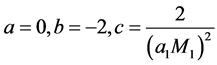
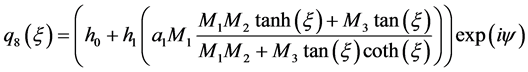
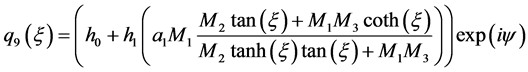


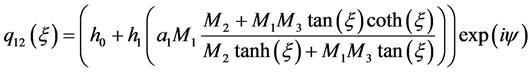

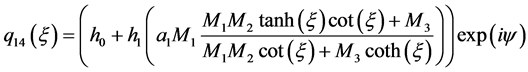
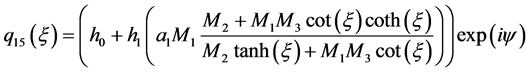 (17)
(17)
其中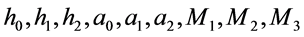 为任意常数。
为任意常数。
4. 主要结论
本文中我们对新辅助方程 进行四类函数的求解,成功获得了三角函数、双曲函数、指数函数、Jacobi椭圆函数,将其应用于带有扰动项的非线性Schrödinger方程中,获得非线性偏微分方程的相互作用解。研究非线性偏微分方程的相互作用解具有非常重要的现实依据,例如地震波、飓风波、海啸波同时作用时,我们可以通过研究其作用形式可以减弱其破坏程度。获得非线性偏微分方程相互作用解可以使我们更好的描述复杂的非线性物理现象。
进行四类函数的求解,成功获得了三角函数、双曲函数、指数函数、Jacobi椭圆函数,将其应用于带有扰动项的非线性Schrödinger方程中,获得非线性偏微分方程的相互作用解。研究非线性偏微分方程的相互作用解具有非常重要的现实依据,例如地震波、飓风波、海啸波同时作用时,我们可以通过研究其作用形式可以减弱其破坏程度。获得非线性偏微分方程相互作用解可以使我们更好的描述复杂的非线性物理现象。
基金项目
山东省自然科学基金(ZR2010AM014);临沂大学应用数学提高项目。