1. 引言
由于现代智能化发展进程的加快致使各部件在工作量增加,为了不影响系统的正常工作,因此各个系统的可靠性和耐用性理应得到人们的广泛重视。
在文献[1] 中,作者运用Laplace变换分析了一类由常规故障和临界人为错误引起系统故障的可修复系统的平均故障时间,文献[2] 中作者主要讨论了此系统主算子的谱的特征,分析了系统的稳定性,文献[3] 在[1] [2] [4] 结论的基础上,以泛函理论作为测定描述系统可控性的标准,利用Banach空间相关知识对此系统的稳态解是否可以到达期望概率分布的最优控制问题进行分析。
本文在文献 [2] 的基础上进行进一步分析,结合C0半群理论的内容,得到了系统算子是稠定的预解正算子的结论,并且在假设系统算子的共轭算子及其定义域存在的前提下,得到系统算子的增长界为0的结论。进而根据预解正算子的共尾性质以及相关内容,证明了系统算子的谱上界也为0。
2. 系统介绍
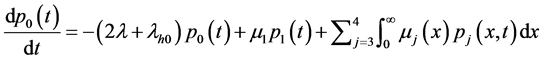

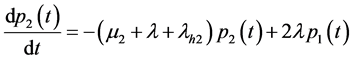

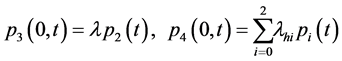
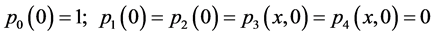
为了方便,记: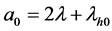 ,
,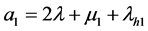 ,
,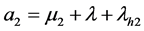 。
。
系统中相关符号的物理意义定义如下:
状态0:两个部件工一个部件储备;
状态1:一个部件故障,储备部件进入工作状态;
状态2:一个部件由于常规和非严重的人为错误引起的故障状态;
状态3:常规错误引起部件故障状态;
状态4:临界人为错误引起的系统故障状态;
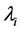 表示运行部件的常数修复率;i = 1,2;
表示运行部件的常数修复率;i = 1,2;
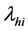 表示从i状态到4状态的常规损坏率;i = 0,1,2;
表示从i状态到4状态的常规损坏率;i = 0,1,2;
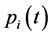 表示t时刻系统处于状态i的概率(i = 0,1,2);
表示t时刻系统处于状态i的概率(i = 0,1,2);
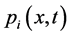 表示t时刻系统处于状态i且已修复时间为x的概率;
表示t时刻系统处于状态i且已修复时间为x的概率;
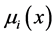 表示状态i到状态0的修复率;
表示状态i到状态0的修复率;
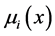 是有界函数(i = 3,4)。
是有界函数(i = 3,4)。
本文对修复率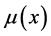 做如下假设:
做如下假设:
1)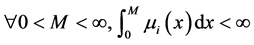 ;
;
2)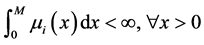 ;
;
3)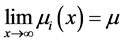 。
。
取状态空间: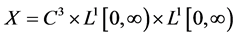 。
。
定义) 有:
有:
则显然X是Banach空间。引入算子:

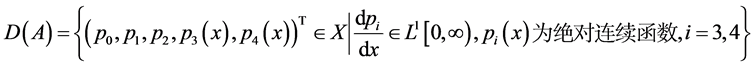
其中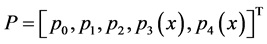 且
且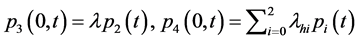
再引入算子:

则有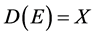 ,此时系统方程组可以改写成Banach空间X中的抽象Cauacy问题[5] :
,此时系统方程组可以改写成Banach空间X中的抽象Cauacy问题[5] :
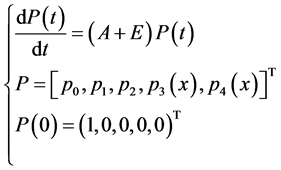
定义1:算子A + E的谱上界s(A + E)的定义为:
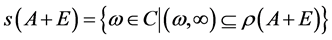
定义2:若算子A + E是半T(t)的无穷小生成元,则增长界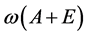 定义为;
定义为;

定义3:E的子集C称为在E中共尾(cofinal),若满足对每个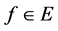 ,存在
,存在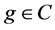 ,使得
,使得 [6] 。
[6] 。
定理1:D(A + E)在X中稠密。
证明:设L={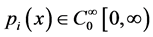
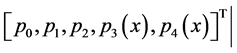 且存在常数
且存在常数 ,使得
,使得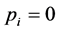 ,
,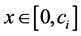 ,
,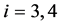 },显然L在X中稠密[7] ,故只需要D(A)在L中稠密。
},显然L在X中稠密[7] ,故只需要D(A)在L中稠密。
取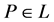 ,则存在
,则存在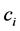 使
使 ,
, ,
, 。令
。令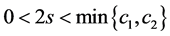 ,显然
,显然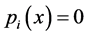 。
。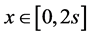 (i=3,4)。根据文献[8] 知:
(i=3,4)。根据文献[8] 知:
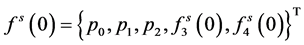
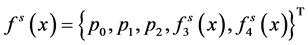
其中:
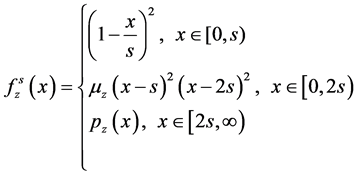
此处:
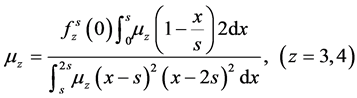
易证: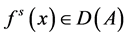 )且:
)且:
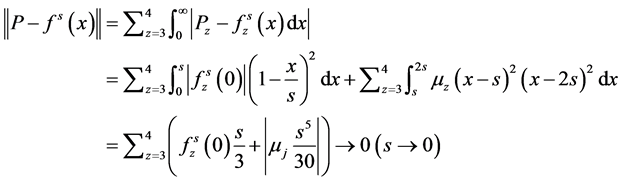
故D(A)在L中稠密,故D(A)在X中稠密。又由于D(E)=X,故D(A)在X中稠密。
定理2:A + E是预解正算子。
证明:对任意给定的y Î X,考虑方程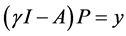 ,等价于如下方程组:
,等价于如下方程组:

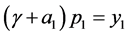
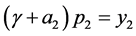
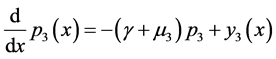

得:
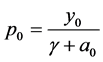
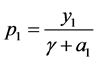
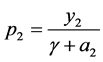
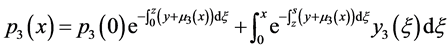
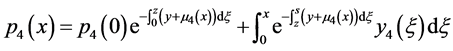
所以:
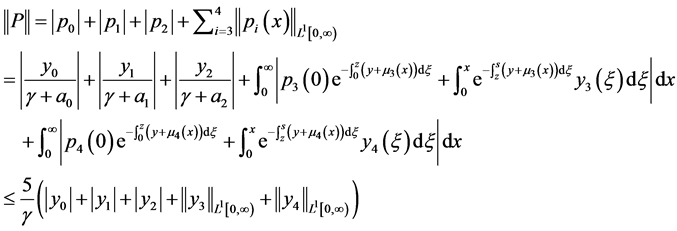
设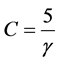 ,因
,因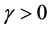 ,故
,故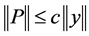 ,所以当
,所以当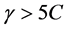 时,
时,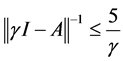 。
。
观察E的表达式,显然E是有界正算子,且设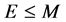 ,有方程
,有方程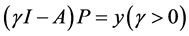 的形式可知,当
的形式可知,当 时,若y为非负向量,则p为非负向量。故
时,若y为非负向量,则p为非负向量。故 为正算子,又
为正算子,又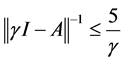 ,故当
,故当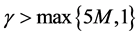 时,
时, 。
。
故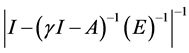 存在且有界。
存在且有界。
因此A + E为预解正算子。
X的共轭空间为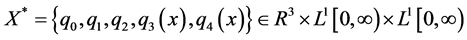 ,其中
,其中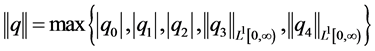 ,显然
,显然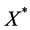 为Banach空间(文献[7] )。因为A + E为X的子空间,X存在共轭空间
为Banach空间(文献[7] )。因为A + E为X的子空间,X存在共轭空间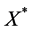 ,则不妨假设
,则不妨假设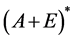 为
为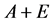 的共轭空间且
的共轭空间且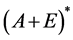 为
为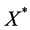 的子空间。
的子空间。
定理3:若算子A是半群T(t)的无穷小生成元,则系统算子所生成的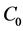 半群的增长界
半群的增长界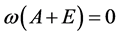 。
。
证明:将系统方程整理为:
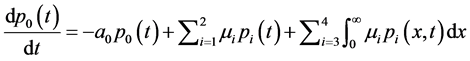
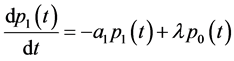
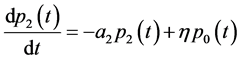
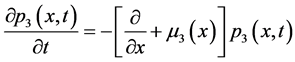

将上式对x从零到正无穷积分,代入边值条件,并将各式左右两端相加,最终可得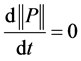 。故系统方程组所对应的半群是非扩张半群,根据初值条件知
。故系统方程组所对应的半群是非扩张半群,根据初值条件知 。故系统算子所生成的
。故系统算子所生成的 半群的增长界
半群的增长界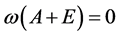 。
。
定理4: 。
。
证明:由前文知,

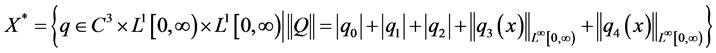
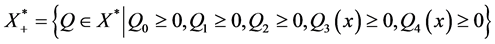
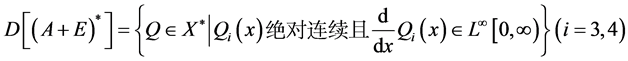
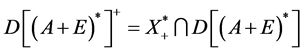
任取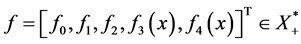 ,则
,则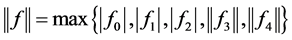 。
。
因此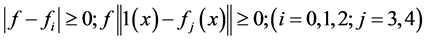 故
故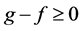 ,所以在
,所以在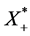 中任取一个元素
中任取一个元素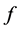 ,
,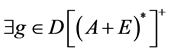 ,使得
,使得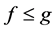 ,则
,则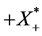 中共尾,又根据定理2可知AE为预解正算子,再由文献[8] ,知:
中共尾,又根据定理2可知AE为预解正算子,再由文献[8] ,知:
基金项目
黑龙江省自然科学基金项目(A201305)。