1. 引言
爆轰[1] -[6] 是一种超声速燃烧。爆轰波以超声速或者高超声速传播, 波后压力和密度明显升高。爆轰波前沿是预压缩冲击波。该冲击波传向炸药并引发剧烈的化学反应,释放出大量化学能[1] 。爆轰波借助迅速释放的化学反应放热实现自持传播。爆轰在工业生产、航空航天、国防建设等方面具有重要应用,比如脉冲爆轰发动机、旋转爆轰发动机、斜爆轰冲压推进和爆轰助推系统的研发已经取得了一系列进展。另外,研究爆轰对于各类爆炸事故的预防和处理等具有重要的现实意义。
本文使用离散玻尔兹曼方法(Discrete Boltzmann Method)研究爆轰问题。离散玻尔兹曼方法与传统的格子玻尔兹曼方法(Lattice Boltzmann Method) [7] 不同。传统的格子玻尔兹曼方法只是偏微分方程组(如Euler方程组、Navier-Stokes方程组等)的一种数值逼近解法。而我们构建和使用的离散玻尔兹曼模型等价于一个Navier-Stokes (NS)模型外加一个关于热动非平衡效应的粗粒化模型。格子玻尔兹曼方法在燃烧模拟方面已有一系列工作[8] -[14] ,但这些工作都落脚于低马赫不可压问题,并且假设化学反应对流场没有影响。最近,我们课题组在燃烧(特别是爆轰)系统的离散玻尔兹曼建模与模拟方面取得一些突破性进展[15] -[18] 。
2. 离散玻尔兹曼模型
2.1. 演化方程
在文献[17] 中,我们构建了比热比和普朗特数可调的多松弛时间(Multiple-relaxation-time)离散玻尔兹曼模型模拟燃烧现象。在玻尔兹曼方程的右侧添加了一个化学项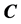 ,表示化学反应引起的分布函数的改变率。通过Chapman-Enskog分析可知,为了恢复带有化学反应的NS方程组,该模型至少需要满足24个独立的矩关系,与之对应,至少需要使用24个离散速度。现在,我们引入另一种化学项的计算形式。可以证明,本模型只需满足16个矩关系就可以恢复相同的NS方程组。这样,离散速度就可以从24个减少为16个,模型的计算效率大幅度提高。
,表示化学反应引起的分布函数的改变率。通过Chapman-Enskog分析可知,为了恢复带有化学反应的NS方程组,该模型至少需要满足24个独立的矩关系,与之对应,至少需要使用24个离散速度。现在,我们引入另一种化学项的计算形式。可以证明,本模型只需满足16个矩关系就可以恢复相同的NS方程组。这样,离散速度就可以从24个减少为16个,模型的计算效率大幅度提高。
离散玻尔兹曼方程的形式如下1
 (1)
(1)
这里,对角矩阵 表示离散速度,下标
表示离散速度,下标 表示离散速度总数,各个离散速度分别为
表示离散速度总数,各个离散速度分别为
 (2)
(2)
其中cyc表示循环排列, 是离散速度
是离散速度 的两个分量,
的两个分量,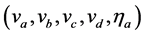 为可调参数。图1给出了离散速度的示意图。
为可调参数。图1给出了离散速度的示意图。
另外, 为离散分布函数,
为离散分布函数, 为离散化的平衡态分布函数,
为离散化的平衡态分布函数, 表示分布函数的矩,
表示分布函数的矩,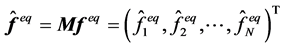 表示平衡态分布函数的矩,并且
表示平衡态分布函数的矩,并且 ,
, ,
, ,
, ,
, ,
, ,
,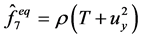 ,
,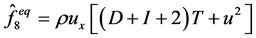 ,
, ,
, ,
, ,
, ,
, ,
,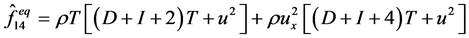 ,
, ,
, ;密度为
;密度为 ,速度为
,速度为 ,温度为
,温度为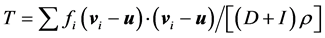 ;
; 是的
是的 逆矩阵,
逆矩阵, 是
是 的矩阵,其元素为
的矩阵,其元素为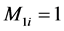 ,
, ,
, ,
,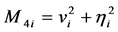 ,
, ,
,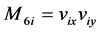 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,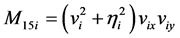 ,
,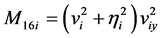 ;
;
 表示空间维度,
表示空间维度, 表示额外自由度数,
表示额外自由度数,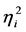 用来描述在额外自由度上的内能。当
用来描述在额外自由度上的内能。当 时,
时, ,否则
,否则 ;对角矩阵
;对角矩阵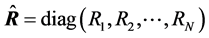 表示松弛因子,其中
表示松弛因子,其中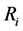 描述了物理量
描述了物理量 松弛到平衡态
松弛到平衡态 的速度;
的速度; 用来修正碰撞项,其中
用来修正碰撞项,其中
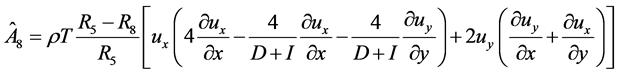 (3)
(3)
 (4)
(4)
化学项 ,其计算方式为
,其计算方式为
 (5)
(5)
图1. 离散速度示意图
式中上标 为随体导数,表示化学反应引起的物理量的变化率,即
为随体导数,表示化学反应引起的物理量的变化率,即 表示化学反应引起的温度的变化率。可以证明,
表示化学反应引起的温度的变化率。可以证明, ,其中
,其中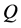 为单位质量的反应物完全反应后释放的化学能,
为单位质量的反应物完全反应后释放的化学能, 为产物的质量分数,
为产物的质量分数,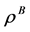 为产物的密度。产物用用符号B表示,反应物用A表示。在化学反应过程,反应物A变成产物B。化学反应进程使用科克伦(Cochran)函数描述,
为产物的密度。产物用用符号B表示,反应物用A表示。在化学反应过程,反应物A变成产物B。化学反应进程使用科克伦(Cochran)函数描述,
 (6)
(6)
式中 为待定可调参数,
为待定可调参数, 为压强。另外,我们引入点火温度
为压强。另外,我们引入点火温度 。当温度
。当温度 大于点火温度
大于点火温度 时,化学反应进行,否则停止。
时,化学反应进行,否则停止。
本模型与文献[17] 的相同点:
本模型的假设条件和应用范围与文献[17] 一致;
演化方程的时间偏微分和空间偏微分的计算方式与文献[17] 一样;
通过Chapman-Enskog分析,本模型可以恢复带有化学反应的可压NS方程组,结果与文献[17] 相同;
可以证明,在一阶精度下,公式(5)给出的化学项与文献[17] 中的化学项一致。
本模型与文献[17] 的不同点:
本模型满足的独立的矩关系只有16个,对应的离散速度为16个,而文献[17] 使用了24个矩关系和24个离散速度;
化学项的计算方法不同;
数值测试表明,在模拟高马赫物理系统时,本模型的数值稳定性要比文献[17] 中的高。
2.2. 非平衡表征
离散玻尔兹曼方程是玻尔兹曼方程在速度空间的特殊离散化形式。玻尔兹曼方程具有描述非平衡系统的本质属性。离散玻尔兹曼方法继承了这一特点。本文引入非平衡表征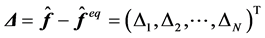 ,并将
,并将
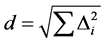 (7)
(7)
作为评估系统偏离平衡态的程度[17] 。因此,当系统处于平衡态时d = 0,否则d > 0。系统偏离平衡态的越远,d越大。可以看出,离散玻尔兹曼方法提供了一个简单有效的方法研究非平衡效应。另外,非平衡表征可用来捕获系统中的各类界面。这是因为,非平衡效应与物理量的梯度密切关联。在界面处,物理量梯度的模急剧增加,非平衡表征随之增强。读者可参考文献[15] -[18] 关于非平衡表征更加详细的叙述。
3. 数值模拟
本文的数值模拟有两部分。在第一部分,为了检测模型的正确性,我们模拟了一维稳定爆轰波,并将数值结果与解析解进行对比。在第二部分,我们模拟了爆轰波激发的RM不稳定性现象,并讨论了四种不同的情形。在下面的数值模拟中,我们使用参数 ,
,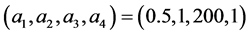 ,
, 控制化学反应。
控制化学反应。
3.1. 稳定爆轰
现在我们模拟一维稳定爆轰现象。初始的物理场为
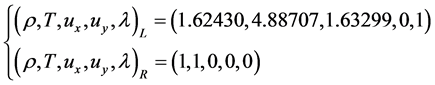 (8)
(8)
其中下标L和R分别代表左侧区域 和右侧区域
和右侧区域 。这里使用的参数为
。这里使用的参数为 ,
, ,
,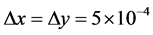 ,
, ,
, ,其它碰撞参数为
,其它碰撞参数为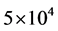 。
。
图2给出了一维稳定爆轰波在演化过程中压强沿x轴的分布情况。图2(a)给出了在时刻t = 0.07、0.08和0.09的DBM数值结果,图2(b)给出了在时刻t = 0.09的DBM数值结果、CJ理论解 [2] [3] 和ZND理论解 [4] - [6] 。根据图(a)的数值结果可知爆轰波的传播速度为4.2,这与解析解4.24870的相对误差为1%。在图2(b)中,爆轰波波后的数值结果为p = 7.91847,与解析解7.93809的相对误差为0.25%。图2(b)显示,在冯·诺依曼峰蜂后DBM的数值结果与与ZND解析解符合的较好。在峰前它们之间存在差异的原因是,ZND理论假设在冯·诺依曼峰处是一个强间断并忽略粘性和热传导的存在,而DBM的数值理论包含粘性和热传导效应。因此我们的数值结果更加真实。
3.2. RM不稳定性
当冲击波经过不同物质的界面时,会对界面产生一个加速度,界面将会获得速度。如果初始界面有扰动,那么在界面附件将会出现Richtmyer-Meshkov (RM)不稳定性现象[19] [20] 。爆轰波是带有化学反应的冲击波。当爆轰波冲击扰动界面时,就会产生RM不稳定性现象。RM不稳定性对爆轰过程有着非常重要的作用。现在模拟爆轰波激发的RM不稳定性现象。数值模拟区域是长 × 宽 = 0.3 × 0.05的长方形,

 (a) (b)
(a) (b)
Figure 2. The pressure versus x in the evolution of a steady detonation: (a) the DBM results at various instants t = 0.07, 0.08, and 0.09; (b) the DBM, CJ and ZND results at time t = 0.09
图2. 一维稳定爆轰波演化过程的压强轮廓图:(a) 在t = 0.07、0.08和0.09时刻的DBM数值结果;(b) 在t = 0.09时刻的DBM数值结果、CJ理论解和ZND理论解
沿x轴分为三个部分: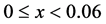 、
、 和
和 。左侧区域是向右传播的稳定爆轰波,中间区域充满了炸药。这两个区域的物理场分布与图2(b)的一样。右侧区域是另一种物质。通过更换右侧区域的物质,我们可以得到不同情形的数值模拟。本文模拟了四种情况。第一种情况,爆轰波由炸药传向较重介质,在重介质中化学反应不再进行;第二种情况,爆轰波由炸药传向较重介质,在重介质中化学反应仍然进行;第三种情况,爆轰波由炸药传向较轻介质,在轻介质中化学反应不再进行;第四种情况,爆轰波由炸药传向较轻介质,在轻介质中化学反应仍然进行。另外,为了激发出RM不稳定性现象,我们在中间区域和右侧区域之间的物质界面上施加了初始扰动
。左侧区域是向右传播的稳定爆轰波,中间区域充满了炸药。这两个区域的物理场分布与图2(b)的一样。右侧区域是另一种物质。通过更换右侧区域的物质,我们可以得到不同情形的数值模拟。本文模拟了四种情况。第一种情况,爆轰波由炸药传向较重介质,在重介质中化学反应不再进行;第二种情况,爆轰波由炸药传向较重介质,在重介质中化学反应仍然进行;第三种情况,爆轰波由炸药传向较轻介质,在轻介质中化学反应不再进行;第四种情况,爆轰波由炸药传向较轻介质,在轻介质中化学反应仍然进行。另外,为了激发出RM不稳定性现象,我们在中间区域和右侧区域之间的物质界面上施加了初始扰动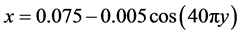 。
。
3.2.1. 第一种情况
我们首先考虑第一种情况:稳定爆轰波由炸药传向另一种不反应的较重介质。这种介质的初始物理量为 。其它数值参数与图2一样。
。其它数值参数与图2一样。
图3给出了RM不稳定性演化过程的密度场,从上到下依次对应时刻t = 0.00、0.01、0.03和0.13。图(a)给出了初始时刻爆轰波从左侧炸药传向右侧一种较重的物质。图(b)显示,由于爆轰波的压缩作用,扰动振幅大幅度减小。之后,振幅开始增长,见图(c)~(d)。在图(d)中可以清晰地看到轻介质中的泡状结构和重介质中的钉状结构。可以看出,RM不稳定性的发展能够促进流体系统中不同介质的相互混合渗透。
图4给出了非平衡表征d在时刻t = 0.00、0.01、0.02、0.03、 0.04、0.05、0.06和0.13的数值结果。图(a)显示,初始时刻在爆轰波附近非平衡表征非常明显。从图(b)~(g)可以清晰地辨认出反射冲击波、物质界面和透射冲击波的演化过程。当平面爆轰波与物质界面相撞后,该爆轰波转变成一个透射冲击波
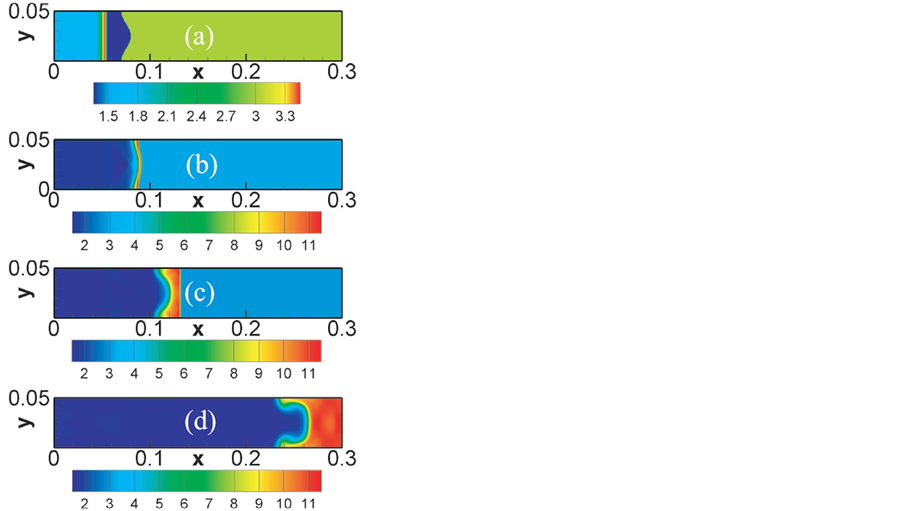
Figure 3. Snapshots of RM instability in the first case. Panels (a)-(d) show the density fields at the times, t = 0.00, 0.01, 0.03, and 0.13, respectively
图3. 第一种情况下的RM不稳定性。(a)~(d)给出了在时刻t = 0.00、0.01、0.03和0.13的密度场
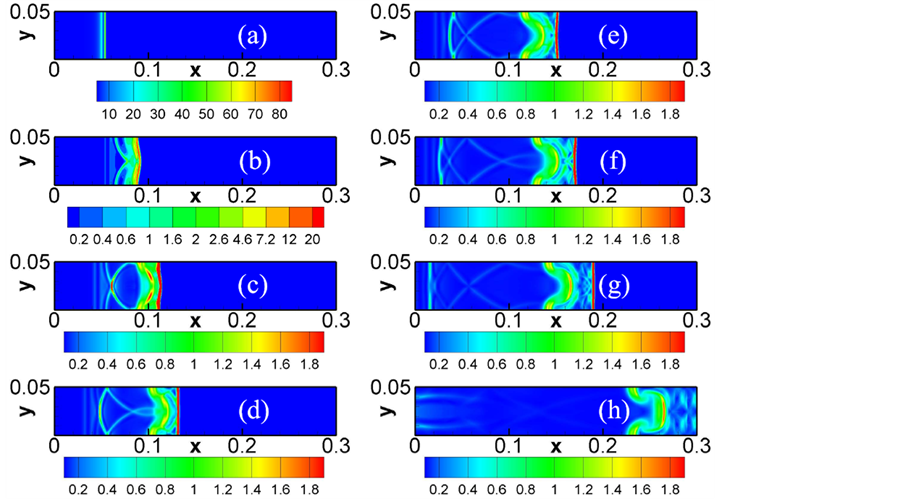
Figure 4. Contours of nonequilibrium manifestation d in the evolution of RM instability in the first case. Panels (a)-(h) are for the times, t = 0.00, 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.13, respectively
图4. 第一种RM不稳定性情况下非平衡表征d的演化图。(a)~(h)依次对应时刻t = 0.00、0.01、0.02、0.03、0.04、0.05、0.06和0.13
和一个反射冲击波。这两冲击波在初始阶段都是曲面波。现在分析反射冲击波的演化过程。如图(b)所示,在计算区域内反射波上下对称。上部分与下部分的反射波在传播过程相互叠加,产生出新的曲面冲击波,见图(b)~(d)。新生的曲面冲击波不断得到后面追来的冲击波的能量补充,其形状不断被矫正,很快变成一个平面冲击波,见图(e)~(g)。透射冲击波的演化机理类似。另外,可以从图(h)看出,在物质界面两侧具有明显的非对称特征。
3.2.2. 第二种情况
现在模拟第二种情况的RM不稳定性:爆轰波由炸药传向较重的介质后继续进行化学反应。在初始时刻,这种较重的介质内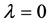 。计算参数
。计算参数 ,其它参数与第一种情况的数值模拟参数一样。在图5中从上到下依次给出了在时刻t = 0.00,0.01,0.03和0.13的密度场。这四个时刻与图3中的四个时刻一致。对比图3和图5可以发现明显的不同:一方面,图3中的透射冲击波传播速度比图5中的传播速度慢,但是图3中的物质界面速度改变量比图5中的大;另一方面,图3中轻介质内气泡体积大于图5中的,相应地,图3中重介质内钉状体积小于图5中的。也就说,与图5相比,图3中RM不稳定性更早地进入非线性阶段。
,其它参数与第一种情况的数值模拟参数一样。在图5中从上到下依次给出了在时刻t = 0.00,0.01,0.03和0.13的密度场。这四个时刻与图3中的四个时刻一致。对比图3和图5可以发现明显的不同:一方面,图3中的透射冲击波传播速度比图5中的传播速度慢,但是图3中的物质界面速度改变量比图5中的大;另一方面,图3中轻介质内气泡体积大于图5中的,相应地,图3中重介质内钉状体积小于图5中的。也就说,与图5相比,图3中RM不稳定性更早地进入非线性阶段。
3.2.3. 第三种情况
本部分模拟第三种情况的RM不稳定性:爆轰波透过物质界面后不再进行化学反应,且物质界面右侧的物质比界面左侧的物质轻。物质界面右侧的物理量为 。数值参数
。数值参数 ,其它参数与第一种情况的数值模拟参数一样。图6给出了在时刻t = 0.000、0.005、0.015、0.020、0.050和0.080的密度场。物理过程如下:当爆轰波扫过物质界面时,在界面两侧分别产生一个向左传播的反射稀疏波和一个向右传播的冲击波。由于在扰动界面波峰左侧的压强比右侧的压强低,所以在压强差的驱动下扰动界面的振幅减小,并导致初始界面的波峰和波谷发生反
,其它参数与第一种情况的数值模拟参数一样。图6给出了在时刻t = 0.000、0.005、0.015、0.020、0.050和0.080的密度场。物理过程如下:当爆轰波扫过物质界面时,在界面两侧分别产生一个向左传播的反射稀疏波和一个向右传播的冲击波。由于在扰动界面波峰左侧的压强比右侧的压强低,所以在压强差的驱动下扰动界面的振幅减小,并导致初始界面的波峰和波谷发生反
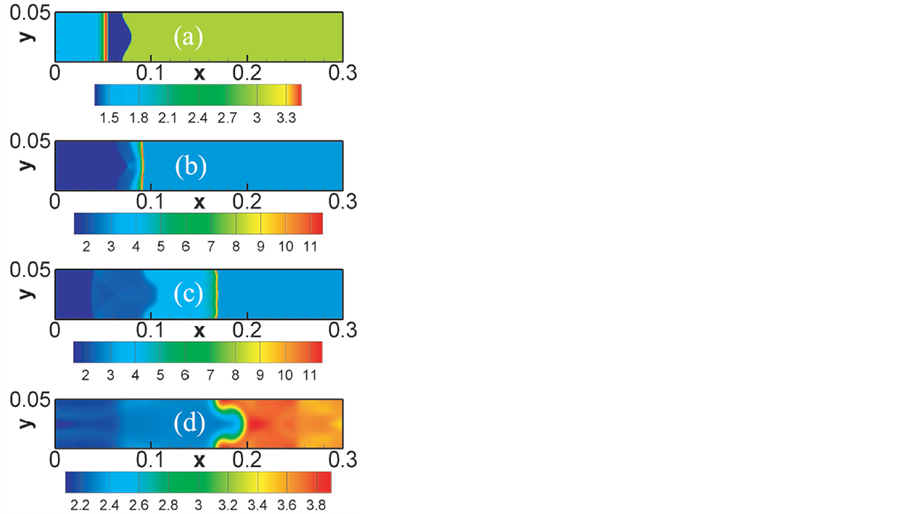
Figure 5. Snapshots of RM instability in the second case. Panels (a)-(d) show the density fields at the times, t = 0.00, 0.01, 0.03, and 0.13, respectively
图5. 第二种情况下的RM不稳定性。(a)~(d)给出了在时刻t = 0.00、0.01、0.03和 0.13的密度场
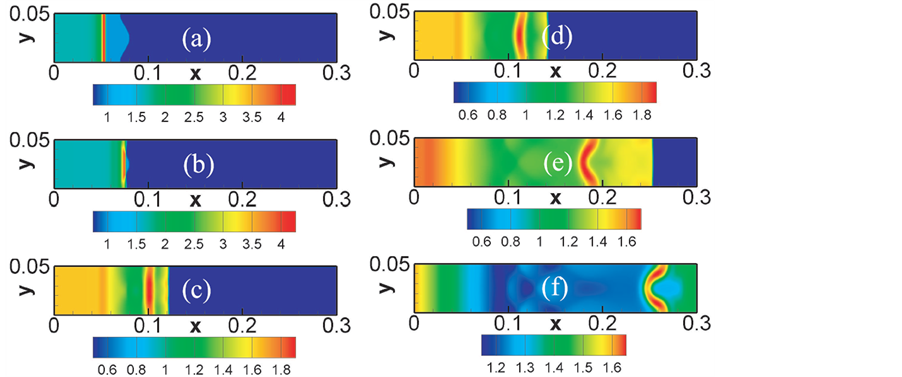
Figure 6. Snapshots of RM instability in the third case. Panels (a)-(f) show the density fields at the times, t = 0.000, 0.005, 0.015, 0.020, 0.050, and 0.080, respectively
图6. 第三种情况下的RM不稳定性。(a)~(f)给出了在时刻t = 0.000、0.005、0.015、0.020、0.050和0.080的密度场
转,见图(a)~(d)。之后,扰动振幅继续发展,经历线性阶段后再进入非线性阶段。从图(d)~(f)可以看出,在界面两侧的不同流体逐渐向彼此渗透。
3.2.4. 第四种情况
最后,我们模拟第四种情况:在物质界面右侧的物质比左侧的轻,并且在爆轰波的冲击压缩下会产生化学反应。图7绘制了密度场的演化过程。下面比较图6和图7的异同点。相同点:爆轰波与物质界面相遇后都会产生反射稀疏波和透射冲击波,并且反射波和透射波在远离物质界面过程逐渐变成平面波;物质界面都会发生反转过程,RM不稳定性现象明显。不同点:图6显示当爆轰波扫过物质界面后,在物质界面附近会出现一个高密度带,其密度明显高于两侧部分,而图7显示当爆轰波扫过物质界面后,从物质界面左侧向右侧系统的密度单调光滑递减。这是因为在图6中,当爆轰波经过物质界面后进入不反应的物质,能量突然降低,温度急剧下降,因而在物质界面形成一个低温区域,在与之相对应处形成一个高密区域。而在图7中,当爆轰波经过物质界面后进入另一种化学物质后,仍然有化学能释放,能量仍有部分补充,温度缓慢下降,密度单调分布。
4. 总结和讨论
本文构建了一个多松弛时间离散玻尔兹曼模型,并使用该模型模拟部分爆轰现象。本模型与文献[17] 的相同点:假设条件和应用范围一致;演化方程的时间偏微分和空间偏微分的计算方式一样;通过Chapman-Enskog分析,可以恢复同样带有化学反应的可压NS方程组,并且比热比和普朗特数可调;在一阶精度下,化学项的处理结果一致。本模型与文献[17] 的不同点:本模型基于16个独立的动理学矩关系,使用16个离散速度,而文献[17] 基于24个矩关系和24个离散速度;化学项的计算方法不同;数值测试表明,在模拟部分高马赫物理系统时,本模型的数值稳定性要比文献[17] 中的高。
使用该模型,本文分四种情况模拟对比了爆轰波在不同情况下激发的Richtmyer-Meshkov不稳定性问题。第一种情况,爆轰波由炸药传向较重介质,在重介质中化学反应不再进行;第二种情况,爆轰波由炸药传向较重介质,在重介质中化学反应仍然进行;第三种情况,爆轰波由炸药传向较轻介质,在轻介质中化学反应不再进行;第四种情况,爆轰波由炸药传向较轻介质,在轻介质中化学反应仍然进行。在第三种情况,由于突然失去能量补充,降温急剧下降,在物质界附近形成一层低温区域,相应地会出现一层高密区域。
需要强调的是,爆轰具有很重要的实际意义。目前,理论推导﹑数值模拟和实验方法已经成为研究爆轰[1] 等诸多学科的三大基本手段。这三大研究方法相互补充﹑相互验证。离散玻尔兹曼方法是介观层次上的数值模拟方法,在模拟研究爆轰现象中的非平衡问题方面具有本质优势。本文模拟了一维稳定爆轰波,并比较了数值结果﹑CJ理论解和ZND理论解。关于爆轰波激发的Richtmyer-Meshkov不稳定性问
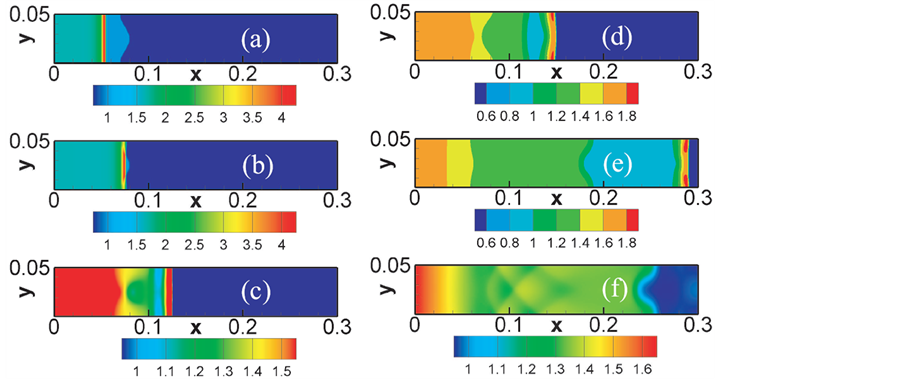
Figure 7. Snapshots of RM instability in the fourth case. Panels (a)-(f) show the density fields at the times, t = 0.000, 0.005, 0.015, 0.020, 0.050, and 0.080, respectively
图7. 第四种情况下的RM不稳定性。(a)~(f)给出了在时刻t = 0.000、0.005、0.015、0.020、0.050和0.080的密度场
题,同样可以将数值结果与理论解或实验结果进行比较。比如,在实验方案中,可以设定爆轰波在预混可燃气体中产生并传播,将惰性气体填充在不反应区域,可以用X光设备测量气体密度并追逐爆轰波界面和物质界面,以及在实验装置中预设压力和温度探测器测量系统的压力和温度。这方面的工作有待进一步研究。
基金项目
本研究得到了计算物理重点实验室基金、国家自然科学基金项目[批准号:11475028和11574390]、中国国家重点基础研究发展计划[批准号:2013 CBA01504]的资助。
NOTES
1在文献[17] 中,公式(1)内修正项 前的符号应为负号(排版错误),其余推导过程是正确的,特此声明。As for Ref. [17], there is a typo on the sign in front of the correction term
前的符号应为负号(排版错误),其余推导过程是正确的,特此声明。As for Ref. [17], there is a typo on the sign in front of the correction term  in Eq. (1). It should be “−”. The remaining derivations are correct.
in Eq. (1). It should be “−”. The remaining derivations are correct.