1. 引言
图像分割是计算机图像识别与理解领域非常活跃的一个分支,是图像处理,图像分析等领域最重要的研究领域[1] -[4] 。人们在对图像的研究和应用中,往往仅对图像中的某些部分感兴趣,为了识别这些具有特殊性质的区域,需要将他们呢分离提取出来,在此基础上才有可能对目标进行更深层次的处理。图像分割就是指把图像分成各具有特征的区域并提取出感兴趣目标的技术和过程。一方面,它是目标表达的基础,对特征的测量有重要的影响。另一方面,图像分割及其基于分割的目标表达,特征的测量有重要的影响;另一方面,图像分割及其基于分割的目标表达,特征提取和参数测量可以将原始图像信息转化为更抽象,更紧凑的形式,使得更高层次的图像分析和理解成为可能。因此图像分割是图像分析和图像识别前期处理的一个重要步骤。
今年来,活动轮廓模型在图像分割中得到广泛的研究与应用 [5] [6] ,该类模型在分割图像是以能量泛函的形式来反映分割区域的位置、大小、形状、等先验知识,确保了曲线在演化过程能够保持连续性和平滑性。
2000年,Chan和Vese提出了梯度无关活动轮廓模型(C-V方法) [7] ,该模型具有自动检测内部轮廓、初始曲线位置选择保持鲁棒形、与梯度无关等优点。C-V方法基于简化的Mumford-Shan模型(简称M-S模型) [8] [9] ,由于该模型是基于图像区域星系的,因此使用与边缘模糊或者是不连续的情况,且对曲线初始位置不敏感。但此方法适用于边缘模糊或者是不连续的情况,且假定图像中仅存在目标和背景两类同质区域。传统的单水平集函数只局限在描述两个相,而描述多相图像分割通常需要用多个水平集函数。多相分割始于1996年Zhao等关于多项运动的研究 [10] ,该方法用m个区域设定m个水平集函数,这样可以表达 相图像,并且可避免水平集函数覆盖区域的“重叠”和“真空(漏盖)”问题 [11] [12] 。
相图像,并且可避免水平集函数覆盖区域的“重叠”和“真空(漏盖)”问题 [11] [12] 。
本文将C-V方法以及Vese-Chan多相水平集法分别应用于多相医学图像的分割,通过对比数值试验结果,显示出多个水平集函数(本文取2个水平集函数)在图像分割中所具有的明显优势。本文主要研究以下几个方面:概述了水平集方法的基本原理及其应用;介绍了简化的C-V模型的基本原理,并且由单水平集函数推广到两个水平集函数,引入了改进的Vese-Chan变分多水平集模型。最后通过一系列的实验,表明两个水平集函数在处理多相图像时的明显优于单水平函数。本文是按照如下方式安排的。第2节主要介绍了水平集方法的基本原理以及C-V模型。第3节在研究多相图像分割的需求上介绍了Vese-Chan变分水平集模型。第4节通过一系列的实验,分别展示了C-V模型以及Vese-Chan变分水平集法处理图像的结果,并且对比了图像分割处理结果的优异。第5节展望了以后研究重点以及多相分割算法。
2. 水平集算法在图像分割中的应用原理
图像分割问题可以用多种数学方法来描述。我们下面介绍其中一种较为实用的方法(由Mumford以及Shah 1989年提出)。设一个观察到的电子图像可以用函数 来表示,并且该函数定义的区域是
来表示,并且该函数定义的区域是
 。我们并设
。我们并设 ,这里
,这里 是区域
是区域 的边界组成的曲线,
的边界组成的曲线, 是一个正整数。那么图像分割问
是一个正整数。那么图像分割问
题可以表述为下面一个最小值问题:我们要找到一个光滑函数 ,使得下面的函数
,使得下面的函数
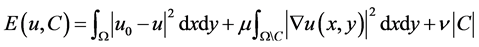
达到最小值。这里|C|表示曲线C的长度, 是给定的常数。上述问题还是难于求解,我们把图像分割问题可以表述为另外一个最小值问题:我们要找到一个分段单值函数,也就是,在
是给定的常数。上述问题还是难于求解,我们把图像分割问题可以表述为另外一个最小值问题:我们要找到一个分段单值函数,也就是,在 上
上 为常值
为常值 ,使得下面的函数
,使得下面的函数
 (2.1)
(2.1)
达到最小值。在下面2.1节讨论的C-V模型中n = 2,它是最简单的一种情形,此时图像函数的定义区域只分为两个区域;在下面2.2节讨论的Vese-Chan变分多水平集模型中我们只考虑了n = 4,此时假定图像函数的定义区域只分为四个区域。
2.1. C-V模型
C-V方法中,假设图像区域 上的演化曲线
上的演化曲线 是
是 的一个子集ω的边界,即
的一个子集ω的边界,即 。设原图像
。设原图像 被任意闭合主动轮廓线
被任意闭合主动轮廓线 划分为内部区域
划分为内部区域 (用inside (C)表示)和外部区域
(用inside (C)表示)和外部区域 (用outside (C)表示)两个同质区域,则能量泛函可写成:
(用outside (C)表示)两个同质区域,则能量泛函可写成:
 (2.2)
(2.2)
其中 为各个能量项权重参数,一般取
为各个能量项权重参数,一般取 。
。 ,
, 是常值,分别表示曲线
是常值,分别表示曲线 内部区域和外部区域的所有像素灰度的平均值。用水平集函数
内部区域和外部区域的所有像素灰度的平均值。用水平集函数 来表示闭合轮廓线
来表示闭合轮廓线 ,即
,即 为
为 的零水平集。关于水平集函数的详细介绍,参见文献 [13] 。
的零水平集。关于水平集函数的详细介绍,参见文献 [13] 。
考虑到Heaviside函数和Dirac函数的形式为:
 (2.3)
(2.3)
 (2.4)
(2.4)
则能量泛函中的各项可以改写成:
 (2.5)
(2.5)
 (2.6)
(2.6)
 (2.7)
(2.7)
 (2.8)
(2.8)
从而Mumford-Shah模型中的能量泛函(2.2)用水平集函数表示可改写为:
 (2.9)
(2.9)
为求出(2.9)中的能量泛函的最小值时,我们根据变分法发现函数必须满足方程
 (2.10)
(2.10)
这里函数写成:
 (2.11)
(2.11)
令 不变,最小化能量函数
不变,最小化能量函数 ,可得到
,可得到 的表达式:
的表达式:
 (2.12)
(2.12)
 (2.13)
(2.13)
其中, 为轮廓内像素的平均灰度值;
为轮廓内像素的平均灰度值; 为轮廓外像素的平均灰度值。在实际求解时,Heaviside函数
为轮廓外像素的平均灰度值。在实际求解时,Heaviside函数 通常用一个函数
通常用一个函数 来代替:
来代替:
 (2.14)
(2.14)
同样的,对Dirac函数也通常用一个函数来代替:
 (2.15)
(2.15)
因为一般较难直接求解静态的偏微分方程(2.10),我们转向求出下面动态的偏微分方程的稳态解:
 (2.16)
(2.16)
理论可以证明(2.16)的稳态解就是静态的偏微分方程2-(10)的解。
我们利用通常的有限差分法来离散(2.16),设空间步长为 ,时间步长为
,时间步长为 ,有如下方程:
,有如下方程:
 (2.17)
(2.17)
这里的 代表图像函数
代表图像函数 的值,在MATLAB中很容易得到它。
的值,在MATLAB中很容易得到它。
2.2. 计算步骤
1) 初始化:定义初始轮廓曲线 ,并根据
,并根据 计算初始的符号距离函数
计算初始的符号距离函数 ;
;
2) 根据当前的 ,计算
,计算 和
和 ,以及轮廓线曲率的值
,以及轮廓线曲率的值 ;
;
3) 根据方程(2.17),求得该点下一时刻的 值,并且更新轮廓线
值,并且更新轮廓线 ;
;
4) 检测迭代是否满足收敛条件,如果收敛,则停止计算,输出最终轮廓线。否则,重复步骤2);
2.3. 小结
本节首先介绍了C-V模型的基本理论以及数值实现方法。C-V模型将图像的分割为目标和背景两个部分,所有与目标平均灰度值接近的像素被划入目标中;而与背景平均灰度相接近的像素则被划入背景中。这样便忽略了目标或背景可能存在的内部亮度的变化,而现实中要处理的图像往往存在着复杂的亮度变化,导致分割失败。因此,接下来我们将引入Vese-Chan变分多水平集模型,该模型含有m个水平集函数,可以用来识别复杂的图像。
3. Vese-Chan变分多水平集模型
3.1. Vese-Chan变分多水平模型的提出
Vese -Chan对C-V模型进行了扩展 [6] ,提出了一种新的基于M-S模型的多相图像分割的Vese-Chan变分水平集模型。在该模型中,用个水平集函数划分图像为 个相,水平集函数的个数可以减少为
个相,水平集函数的个数可以减少为 。
。
对 个水平集函数
个水平集函数 ,引入水平集函数向量
,引入水平集函数向量 和Heaviside函数向量
和Heaviside函数向量 ,则相可以定义成:两像素点
,则相可以定义成:两像素点 和
和 属于同一相中,当且仅当
属于同一相中,当且仅当 。即决定了每一个分割部分或相。一幅图像的
。即决定了每一个分割部分或相。一幅图像的 有个可能值,在一个区域
有个可能值,在一个区域 中就可以定义个相。因此,被分成不相交的
中就可以定义个相。因此,被分成不相交的 的部分,每个像素
的部分,每个像素 都只属于其中一部分,从而避免了重叠(overlap)或真空(vacuum)问题。用I来表示图像的相,
都只属于其中一部分,从而避免了重叠(overlap)或真空(vacuum)问题。用I来表示图像的相, ,设
,设 ,这里
,这里 为第
为第 相中的平均值,设为
相中的平均值,设为 每一相的特征函数,则可以改写能量泛函数为:
每一相的特征函数,则可以改写能量泛函数为:
 (3.1)
(3.1)
如图1所示 [6] ,左边的图使用了两个水平集函数 实现了4-相分割,曲线
实现了4-相分割,曲线 和
和 将整个区域分为
将整个区域分为 ,
, ,
, ,
, 四个子区域。右边的图用三个
四个子区域。右边的图用三个

Figure 1. Vese-Chan variational level set region partition principle
图1. Vese-Chan变分水平集模型区域划分原理
水平集函数 实现了8-相分割,曲线
实现了8-相分割,曲线 ,
, 和
和 将整个区域分为
将整个区域分为 ,
, ,
, ,
, ,
, ,
, ,
, ,
, 八个子区域。
八个子区域。
这样,Vese-Chan变分水平集模型的能量泛函用水平集函数表示可写成:
 (3.2)
(3.2)
其中 是一个常向量,
是一个常向量, 。函数
。函数 可以写成:
可以写成:
 (3.3)
(3.3)
给定初始条件 ,
, ,于是能量泛函(3.2)的Euler-Lagrange方程写成:
,于是能量泛函(3.2)的Euler-Lagrange方程写成:
 (3.4)
(3.4)
 (3.5)
(3.5)
 (3.6)
(3.6)
 (3.7)
(3.7)
为求出(3.2)中的能量泛函的最小值时,我们根据变分法发现函数 必须满足方程
必须满足方程
 (3.8)
(3.8)
 (3.9)
(3.9)
为了求出上面的函数 ,我们转向求出下面动态的偏微分方程组的稳态解:
,我们转向求出下面动态的偏微分方程组的稳态解:
 (3.10)
(3.10)
 (3.11)
(3.11)
理论可以证明偏微分方程组(3.10)以及(3.11)的稳态解就是静态的偏微分方程(3.8)以及(3.9)的解。
3.2. Vese-Chan变分多水平集模型的数值算法步骤
1) 设定初始值 ,初始水平集
,初始水平集 ,
, 。
。
2) 按照公式(3.4),(3.5),(3.6),(3.7),计算 ,
, ,
, ,
, ;再计算
;再计算 ,
, ;
;
3) 若达到稳定的状态,停止迭代;否则,转到步骤2)。
3.3. Vese-Chan变分多水平集模型的差分格式
在3.2中步骤(2)计算时,采用以下有限差分格式来处理,设
 (3.12)
(3.12)
 (3.13)
(3.13)
 (3.14)
(3.14)
 (3.15)
(3.15)
 (3.16)
(3.16)
 (3.17)
(3.17)
则
 (3.18)
(3.18)
相似的,设
 (3.19)
(3.19)
 (3.20)
(3.20)
 (3.21)
(3.21)
 (3.22)
(3.22)
 (3.23)
(3.23)
 (3.24)
(3.24)
对于第二个水平集函数 :
:
 (3.25)
(3.25)
以上即为Vese-Chan变分多水平集模型的数值实现过程。这里我们采用标准的有限差分法,在下一节中,我们即通过数值试验分割的结果来具体的分析两种模型在分割复杂的多相图片,从而对比判别两种模型的优劣。
4. 数值实验结果与分析
4.1. 实验一
文中的实验平台为IBM Thinkpad T41:Intel Pentium M 1.6GHz,1GB内存,显卡为ATI 7500。运行环境为MatlAB7.0。
采用图像fourblock_gray.bmp,图像大小为 ,其中三个分割目标灰度值不同。首先采用传统的C-V模型。给定参数如下:
,其中三个分割目标灰度值不同。首先采用传统的C-V模型。给定参数如下: ,面积权系数
,面积权系数 ,轮廓线长度权系数
,轮廓线长度权系数 ,时间步长
,时间步长 ,空间离散步长
,空间离散步长 ,规整化Dirac函数和Heaviside函数所用参数
,规整化Dirac函数和Heaviside函数所用参数 。为了得到较好的分隔效果,我们循环1000次,由图2分割结果来看,分割效果很不理想,在只有一个水平集函数的条件下,只能识别出两相图像轮廓,而此次实验图片为四相图片,只能勾勒出黑色矩形的边框,效果不大好。
。为了得到较好的分隔效果,我们循环1000次,由图2分割结果来看,分割效果很不理想,在只有一个水平集函数的条件下,只能识别出两相图像轮廓,而此次实验图片为四相图片,只能勾勒出黑色矩形的边框,效果不大好。
而我们再次采用改进的Vese-Chan变分多水平集模型,参数设计如上,循环500次,由图3可以看到,该方法非常有效。
4.2. 实验二
采用的是图像knee1.jpg四相图片。图4为传统的C-V模型分割效果,实验参数: ,
, ,轮廓线长度权系数
,轮廓线长度权系数 ,时间步长
,时间步长 ,空间离散步长
,空间离散步长 ,
, 。循环次数为200次。
。循环次数为200次。
观察分割效果,可以看出C-V模型分割出来了膝关节外围的大体轮廓;但是在膝关节内侧,以及关节接触点没有被分割识别出来。为此我们采用改进的Vese-Chan变分水平集模型。参数同上,同样循环200次,得到结果图5可以看出,分割效果较好。
可以看出,内侧的轮廓以及膝关节接触处轮廓都被很好的识别分割出来。
 (a) 初始时刻 (b) 最终分割结果
(a) 初始时刻 (b) 最终分割结果
Figure 2. Pictures processing by C-V model
图2. C-V模型处理四相图片
 (a) 初始时刻(b) 最终分割结果
(a) 初始时刻(b) 最终分割结果
Figure 3. Pictures processing by two level sets model
图3. 两个水平集模型处理四相图片
 (a) 初始时刻(b) 最终分割结果
(a) 初始时刻(b) 最终分割结果
Figure 4. Pictures processing by C-V model
图4. C-V模型处理四相图片
 (a) 初始时刻(b) 最终分割结果
(a) 初始时刻(b) 最终分割结果
Figure 5. Pictures processing by two level set functions model
图5. 两个水平集函数模型处理四相图片
5. 总结与展望
本论文针对多相图像分割的变分水平集法及其相关数学模型进行了系统的研究,并以实例说明其优势。得出如下结论:
1) 简单的C-V方法只有一个水平集函数,在处理两相图像时,效果是很好的,甚至分割精度比多个水平集函数分割效果要好得多。但是多相(大于2相)图像分割中,单个水平集函数只能识别其中的两相,而自动忽略了其他的相。多个水平集函数由于计算量大,在试验中,耗费时间要大一些。
2) 实验参数的选取对于实验的时间以及结果有着决定性的作用。C-V模型参数的选取中,初始水平集函数为一个圆,当圆心的位置为图像的正中间的那个点时,效果最优。Vese-Chan多相水平集法的初始水平集函数为两个圆,圆的大小需要依照图像的大小作相应的调整,而且当实验图像格式比较大时,异常耗时。
3) 从Vese-Chan多水平集法的表达式可以看出,尽管只是使用两个水平集函数实现四相分割,其表达式的形式已经很复杂,若要实现大于四相的图像分割,单单是推导表达式就相当繁重,因而迫切的需要找出一个通用的表达式,以清晰明了的表达分割。这也将是下一步研究的重点。
致谢
本文从选题到完成,都是在王汉权老师的指导下完成的。倾注了老师大量的心血,再次致以衷心的感谢与真挚的敬意。同时感谢支持以及给予帮助的同学和朋友们,感恩,谢谢!
基金项目
本文受到云南省科技厅中青年学术带头人后备人才基金、国家自然科学基金(11261065)等资助。