1. 引言
量子Zeno效应是对一个不稳定的系统进行足够频繁的测量之后,这个系统始终处于初始状态,或者与不测量相比它的衰减速率会很慢的现象。量子Zeno效应(QZE)最先被Misra和Sudarshan提出来 [1] ,此后量子Zeno效应得到国内外广大研究者的关注,并对这种现象进行了不同方面的研究。Cook在理论上提出量子Zeno效应可以被观测到 [2] 。之后不久Itano等人根据Cook的理论在实验上观测到量子Zeno效应 [3] 。此后,在许多不同的物理系统中都证实了该效应的存在,如光子偏振 [4] 、腔量子电动力学 [5] 、玻色爱因斯坦凝聚态 [6] 、中子自旋 [7] 以及核磁共振系统 [8] 等等。在近几年对量子Zeno效应的研究取得了巨大进步,其中Francica等人提出在振荡腔中两原子的频率对称失谐,会产生量子Zeno效应和反Zeno效应 [9] ;David和MArtin-Martínez等人提出在有限频率中通过非投影测量而得出类-Zeno效应 [10] ;Peise和Lücke等人用激光束实现没有相互作用的测量,产生间接的量子Zeno效应,从而抑制超冷原子的衰减 [11] 等。随着量子信息技术的发展,可以相信量子Zeno效应会在更多方面得到应用。
另一方面,量子纠缠自从被Einstein,Podolsky,Rosen [12] 和SchrÖdinger [13] 提出以来,经过多年研究,它在量子信息和量子物理基本问题研究中扮演者重要角色。量子纠缠已被广泛应用于量子隐形传态,量子密码和量子通讯等量子信息处理过程 [14] 。可以说没有量子纠缠现象就没有今天的量子信息学。因此,研究两体纯态以及多体系之间的量子纠缠对量子信息处理具有重要的意义。这方面已经取得了一系列研究成果,比如:Cirac和Zoller提出基于囚禁离子的量子信息方案 [15] ;Yang和Li等人提出一个改进的两离子纠缠态并发度直接测量方案 [16] ;Maniscalco等得出量子Zeno效应保护量子纠缠 [17] ;Abanin和Demler在冷原子系统中用量子态交换测量一般多体系统的纠缠熵 [18] 。
本文针对原子-场相互作用系统,在JC模型下,考虑单模场处于Fock态下,研究了频繁测量与原子-场间纠缠度的关系。重点分析在不同的测量时间间隔下,改变失谐度的大小对原子-场纠缠度与初态存活几率变化趋势的影响。
2. 理论描述
为了讨论的完整性,我们下面对JC模型和相关概念做简要回顾。
2.1. 系统模型与能量本征态的纠缠度
JC模型假设在高Q腔中嵌入一个二能级原子,然后注入单模辐射场,使原子和光场通过光子共振产生相互作用。系统的哈密顿量在旋波近似(RWA)下可表示为(这里令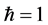 ):
):
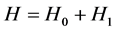 (1)
(1)
其中,
 (2)
(2)
 (3)
(3)
 是单模场与二能级原子的哈密顿量,
是单模场与二能级原子的哈密顿量, 表示单模场与二能级原子之间相互作用,
表示单模场与二能级原子之间相互作用,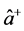 、
、 分别表示场中的产生算符和湮灭算符,
分别表示场中的产生算符和湮灭算符, 、
、 分别表示原子能级的频率间隔和场的频率,
分别表示原子能级的频率间隔和场的频率,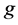 表示原子和场之间相互作用耦合系数,
表示原子和场之间相互作用耦合系数,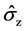 、
、 、
、 分别为原子的能级反转算符以及能级的升降算符。
分别为原子的能级反转算符以及能级的升降算符。
这里我们考虑单模场为Fock态,初始光子数为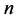 。假设在
。假设在 时,原子处于激发态,即
时,原子处于激发态,即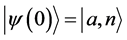 ,那么该系统在任意时刻的波函数可以表示为:
,那么该系统在任意时刻的波函数可以表示为:
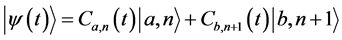 (4)
(4)
(4)式代入薛定谔方程,容易推出能量本征值是:
 (5)
(5)
 (6)
(6)
其中,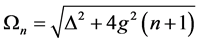 ,
, 。
。
(5)和(6)式对应的本征态分别为:
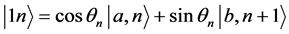 (7)
(7)
 (8)
(8)
其中,
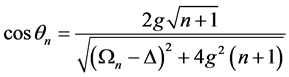 (9)
(9)
 (10)
(10)
为了研究原子与场间的纠缠度,需要计算原子和场的熵。由于本文讨论的原子和场构成的复合系统是纯态,纠缠度可以用Von Neumann熵来表示,其定义为:
 (11)
(11)
其中 是给定量子系统的密度算符,这里令玻尔兹曼常数为1。若量子系统的密度算符
是给定量子系统的密度算符,这里令玻尔兹曼常数为1。若量子系统的密度算符 本征值谱为
本征值谱为 ,因此熵可以写成:
,因此熵可以写成:
 (12)
(12)
因此,能量本征态(7)和(8)式的纠缠度为:
 (13)
(13)
2.2. 量子Zeno效应
上面我们给出了在给定情况下原子-场的纠缠度,现在我们来看此系统经过一系列测量后的变化。由该系统在任意时刻的波函数((4)式),利用薛定谔方程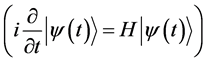 得到波函数随时间演化的概率幅
得到波函数随时间演化的概率幅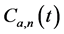 、
、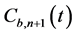 ,其表达式为:
,其表达式为:
 (14)
(14)
 (15)
(15)
因此可以得到经过时间 演化后,系统处在初态的概率为:
演化后,系统处在初态的概率为:
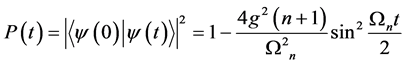 (16)
(16)
下面我们给出对系统经过频繁和连续测量后的结果。设瞬时的理想投影测量的时间间隔为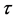 ,经过
,经过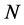 次测量后,处于初态为激发态
次测量后,处于初态为激发态 的初态存活概率为:
的初态存活概率为:
 (17)
(17)
当测量时间间隔 足够小且满足
足够小且满足 时,取近似得到处于激发态
时,取近似得到处于激发态 的初态存活概率为:
的初态存活概率为:
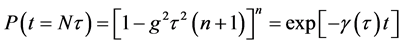 (18)
(18)
这里有效衰减率 。
。
3. 分析与讨论
通过上面的理论计算,现在我们分析原子和辐射场相互作用的JC模型下,单模场为Fock态,频繁测量与原子-场纠缠度的关系。
作为比较,我们做出图1,是对系统没有进行测量时,原子初态存活几率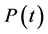 随时间
随时间 的变化,这
的变化,这
 (a) (b)
(a) (b)
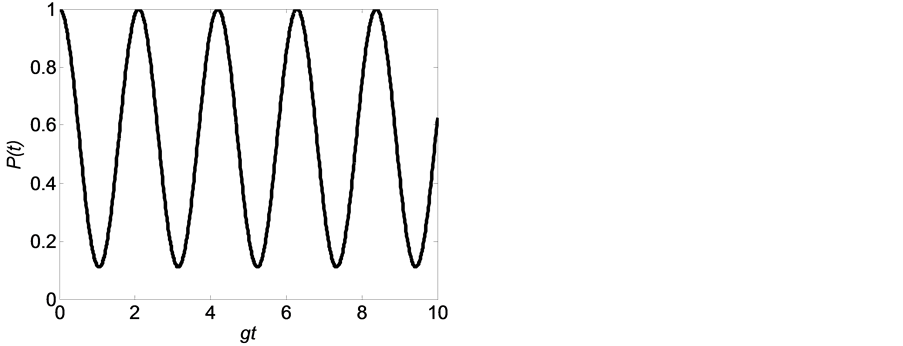
Figure 1. The change of survival probability P(t) with time gt in the case of no measurement for the system. Photon number n in the field is one; the detuning degree is Δ/g and the atom is in the excited state, (a) n = 1, Δ/g = 0; (b) n = 1, Δ/g = 1
图1. 对系统没有测量时,原子初态存活几率P(t)随时间gt的变化。场中的光子数n为1,Δ/g代表失谐度,原子的初始态是激发态,(a) n = 1,Δ/g = 0;(b) n = 1,Δ/g = 1
里我们仅考虑初始场中有一个光子(即n = 1)。从图1中可以看到原子的初态存活几率随时间作拉比震荡,具有周期性的回复和崩塌特性。比较图1(a)和(b)可以看出,随着失谐度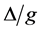 变大,初态存活几率的震荡频率变快。
变大,初态存活几率的震荡频率变快。
图2(a)与(b)是对系统进行多次测量,在不同测量时间间隔 与失谐度
与失谐度 时,原子的初态存活几率
时,原子的初态存活几率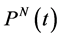 随时间
随时间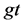 的演化。图2(c)是原子-场间的纠缠度
的演化。图2(c)是原子-场间的纠缠度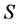 (见(13)式)随失谐度
(见(13)式)随失谐度 的变化趋势。由图2(a)可以看出当测量时间间隔较大时(如图
的变化趋势。由图2(a)可以看出当测量时间间隔较大时(如图 ),原子的初态存活几率具有很明显的衰减现象,并随着
),原子的初态存活几率具有很明显的衰减现象,并随着 的变化衰减为0,此时震荡现象消失。同时可以看出当失谐度
的变化衰减为0,此时震荡现象消失。同时可以看出当失谐度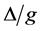 取不同值时,原子的初态存活几率衰减速率明显不同,
取不同值时,原子的初态存活几率衰减速率明显不同, 的取值越小衰减速率越快。图2(b)中显示,当测量时间间隔较小时(如图
的取值越小衰减速率越快。图2(b)中显示,当测量时间间隔较小时(如图 ),原子的初态存活几率衰减速率减缓,并趋近于1产生量子Zeno效应。当失谐度
),原子的初态存活几率衰减速率减缓,并趋近于1产生量子Zeno效应。当失谐度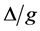 取不同值时,原子的初态存活几率衰减速率趋向相同。图2(c)中可以看出当失谐度
取不同值时,原子的初态存活几率衰减速率趋向相同。图2(c)中可以看出当失谐度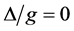 时纠缠度为1,纠缠度
时纠缠度为1,纠缠度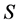 处于最大值。随着失谐度
处于最大值。随着失谐度 增大纠缠度逐渐减小。比较图2(a)与图2(b)可以证明当测量时间间隔很小时失谐度
增大纠缠度逐渐减小。比较图2(a)与图2(b)可以证明当测量时间间隔很小时失谐度

 (a) (b)
(a) (b)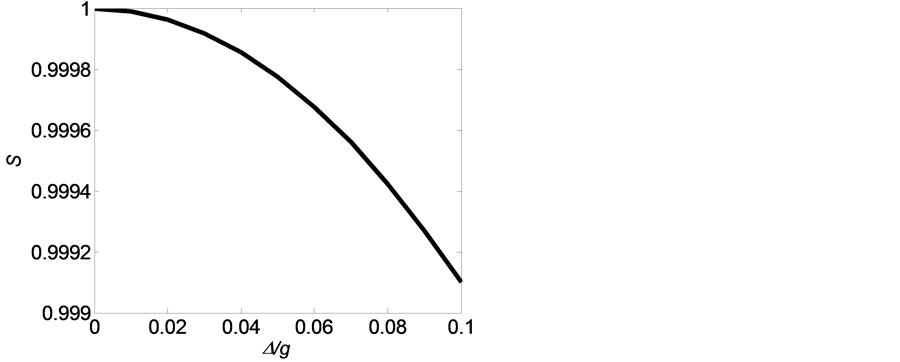 (c)
(c)
Figure 2. (a) and (b) represent the change of survival probability PN(t) with the time gt in different time-intervals gτ after measurements for the system ((a) gτ = 10;(b) gτ = 0.001). The detuning degree is Δ/g and the atom is in the excited state (n = 1, Δ/g = 0: solid line, n = 1, Δ/g = 0.05 dashed line, n = 1, Δ/g = 0 :dotted line). (c) represents the tendency of energy eigenstates of the entanglement S with the detuning degree Δ/g
图2. (a)与(b)是对系统进行测量后,在不同的测量时间间隔gτ时((a) gτ = 10; (b) gτ = 0.001),原子的初态存活几率PN(t)随gτ的变化。Δ/g代表失谐度,原子的初始态是激发态。(图中实线代表n = 1,Δ/g = 0.1,虚线代表n = 1,Δ/g = 0.05,点线代表n = 1,Δ/g = 0)。(c)中实线代表能量本征态纠缠S随失谐量Δ/g的变化趋势
 对初态存活几率的演化影响较小。只有在测量时间间隔很大时才会有明显的影响。比较图2(a)和图2(c)可以看出失谐度
对初态存活几率的演化影响较小。只有在测量时间间隔很大时才会有明显的影响。比较图2(a)和图2(c)可以看出失谐度 变大原子-场能量本征态的纠缠度与测量后的初态存活几率衰减率均变小。
变大原子-场能量本征态的纠缠度与测量后的初态存活几率衰减率均变小。
4. 结论
在原子和辐射场相互作用的JC模型下,单模场为Fock态,我们研究了频繁测量与原子-场间纠缠度的关系。从结果可以看出,在对系统没有进行测量时,原子的初态存活几率随时间作拉比震荡,具有周期性的回复和崩塌特征,失谐度越大初态存活几率的震荡频率越快,这是众所周知的结果。系统进行测量后,当测量时间间隔较大时,初态存活概率的衰减很快并衰减为零。随着测量的时间间隔的减小,初态存活几率的曲线越来越接近1,产生量子Zeno效应,初态存活几率的衰减速率接近零。失谐度变大,纠缠度与测量后的初态存活几率衰减率均变小,即改变失谐度的大小使原子-场纠缠度与初态存活几率的变化趋势一样。结果得出,频繁的测量可以抑制初态存活几率的衰减。原子-场纠缠度与初态存活几率存在一定的联系。
基金项目
国家自然基金资助项目(61271011)。