1. 引言
目前,超临界机翼已广泛使用于新型飞行器的设计中,为了提高飞行性能减少起飞重量,飞机结构大量采用碳纤维复合材料,在机翼布局上普遍采用大展弦比或超大展弦比机翼来提高飞机的升阻比,这种机翼在受到气动载荷时,往往会产生较大的静气动弹性变形,这些变形严重影响着飞机的飞行性能,对飞机的飞行安全造成极大的危害。但是采用超临界机翼后,机翼的静气动弹性特性有什么变化规律,目前尚没有仔细的研究和较多相关文献发表。因此,在新型飞机设计中必须对超临界机翼静气动弹性问题加以认真考虑,以往以刚性飞机为设计对象,辅之以弹性修正的设计方法已不能适应新型飞机的设计要求,需要以真实弹性飞机为研究对象直接进行飞行器气动弹性特性研究和载荷分析 [1] ,由于要求跨音速飞行,甚至大迎角飞行,以前采用的线性气动力理论计算结构弹性对载荷影响的方法不再适用,基于Euler/NS方程的气动力数值计算方法可以满足新型飞机载荷分析的要求,同时,以Euler/NS方程为基础的载荷分析方法,也是目前国内外气动弹性研究发展的热点之一 [2] 。
本文以Euler方程为控制方程,计算弹性机翼飞行时所受气动力载荷,再耦合结构静平衡方程,通过多次迭代计算,求解飞行状态下机翼结构弹性平衡时的真实形状和真实载荷,并以普通弹性机翼和超临界弹性机翼在总载荷保持不变的情况下比较它们的真实弹性变形,从而总结出超临界机翼静气动弹性变化规律。
2. 气动力数值计算方法
主控方程
本文所采用的控制方程是ALE(Arbitrary Lagrangian-Eulerian)描述下的三维可压缩积分形式的Euler方程 [3] [4] ,其在直角坐标系下积分形式为:
 (1)
(1)
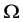 是控制体,
是控制体,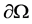 是控制体边界,n为控制体边界外法向单位向量,守恒项和对流项分别为:
是控制体边界,n为控制体边界外法向单位向量,守恒项和对流项分别为:
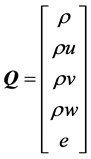 ,
, (2)
(2)
其中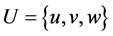 ,
,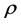 、
、 、
、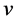 、
、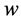 、
、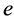 分别为流体的密度、x,y和z轴方向的流体速度和单位体积流体的总内能,nx,ny,nz是n的3个分量。
分别为流体的密度、x,y和z轴方向的流体速度和单位体积流体的总内能,nx,ny,nz是n的3个分量。
2.2.数值求解方法
采用中心有限体积法进行空间离散 [5] ,引入人工粘性后的离散表达式为:
 (3)
(3)
式中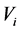 是网格单元体积,
是网格单元体积, 是网格单元内各物理量平均值,
是网格单元内各物理量平均值, 为网格单元通量项,
为网格单元通量项, 为人工粘性项。引入当地时间步长和隐式残值光顺的加速收敛措施后,采用四步龙格–库塔方法,对(3)式进行时间推进求解 [6] 。计算的物理空间生成非结构四面体网格,采用弹簧近似的动网格方法耦合机翼弹性变形 [7] [8] 。
为人工粘性项。引入当地时间步长和隐式残值光顺的加速收敛措施后,采用四步龙格–库塔方法,对(3)式进行时间推进求解 [6] 。计算的物理空间生成非结构四面体网格,采用弹簧近似的动网格方法耦合机翼弹性变形 [7] [8] 。
3. 机翼弹性变形的求解方法
本文采用结构影响系数法 [9] 求解机翼结构系统弹性变形。首先,通过结构有限元分析方法得到机翼的结构柔度影响系数。
在小变形的假设下,机翼表面结构上任一点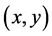 处的变形可写为:
处的变形可写为:
 (4)
(4)
其中 为
为 点处的法向变形,
点处的法向变形, 为结构柔度影响系数,
为结构柔度影响系数,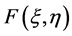 为作用于
为作用于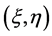 处的载荷,主要可分为气动力和惯性力。
处的载荷,主要可分为气动力和惯性力。
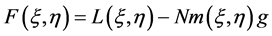 (5)
(5)
其中 为作用于
为作用于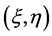 处的气动力,N是过载系数,
处的气动力,N是过载系数, 是
是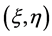 的质量,
的质量,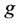 为重力加速度。
为重力加速度。
写成矩阵为:
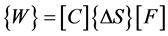 (6)
(6)
机翼表面的坐标加上相应位置的变形,就得到新的表面坐标。
静气动弹性变形的求解是一个耦合迭代过程 [10] ,本论文采用松耦合的方法,通过求解Euler方程得到气动力,再耦合结构静平衡方程计算变形,计算变形后再重新生成网格计算气动力,然后再计算变形,如此循环计算直到变形和气动力都收敛,则得到飞行器最后的弹性平衡状态。
4. 算例及结果分析
4.1. 中等展弦比后掠机翼的静气动弹性变形计算
为了验证本文发展的气动力计算的准确性及弹性变形的求解方法,对一中等展弦比后掠机翼进行了刚性时气动力、弹性时静气动变形的计算。计算状态为:Ma = 0.84,a = 3.06。
从图1本文计算的机翼刚性状态下的展向升力系数与文献 [11] 上风洞试验结果和全速势方程计算结果比较可以看出,本文方法计算结果好于全速势方程计算结果,更接近于风洞试验结果,表明本文发展的气动力计算方法是比较精确的。
从图2可以看出,弹性机翼附加力使机翼产生了负的扭转角,使机翼展向各剖面顺气流方向迎角减少了,从而使弹性机翼的剖面升力系数小于刚性机翼的剖面升力系数,这个结果可以从图3清楚的看到。这些计算结果表明,本文发展的弹性变形求解方法是可行的。
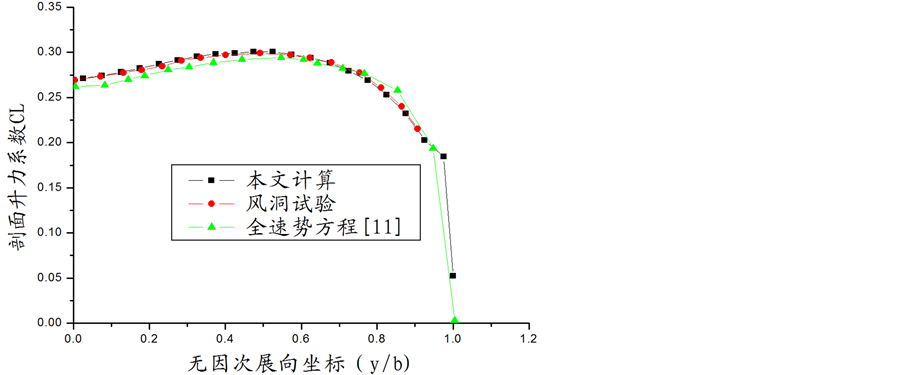
Figure 1. Spanwise lift coefficient curve of rigid wing
图1. 刚性机翼展向升力系数曲线

Figure 2. Elastic wing span wise section torsion angle
图2. 弹性机翼展向剖面扭转角变形
4.2. 超临界机翼的静气动弹性变形计算
为了研究超临界机翼的静气动弹性变形特性,本文研究了两个机翼(平直机翼、后掠机翼),其翼剖面均采用超临界翼型RAE2822,为了和普通翼型的机翼静气动弹性变形特性作比较,相应地计算了保持总升力不变条件下机翼采用普通翼型(NACA64A010, NACA0012)的静气动弹性变形,计算机翼的主要几何参数如表1,计算状态为:Ma = 0.80,a = 1.80。
超临界翼型、普通翼型的平直弹性机翼的扭转变形和刚轴挠度分别为图4、图5;超临界翼型、普通翼型的后掠弹性机翼的扭转变形和刚轴挠度分别为图6、图7。由图可见:带超临界翼型的平直机翼的扭转变形为负值,而普通翼型机翼为正值,且超临界翼型的平直机翼的刚轴挠度小于普通翼型机翼;超临界翼型的后掠机翼和普通翼型的后掠机翼扭转变形均为负值,且带超临界翼型的后掠机翼的扭转变形负值更大,即低头变形更大。
两个机翼各采用两种翼型(超临界翼型和普通翼型)的静气动弹性变形的计算结果表明:带超临界翼型

Table 1. Main geometric parameters of computer wing
表1. 计算机翼的主要几何参数
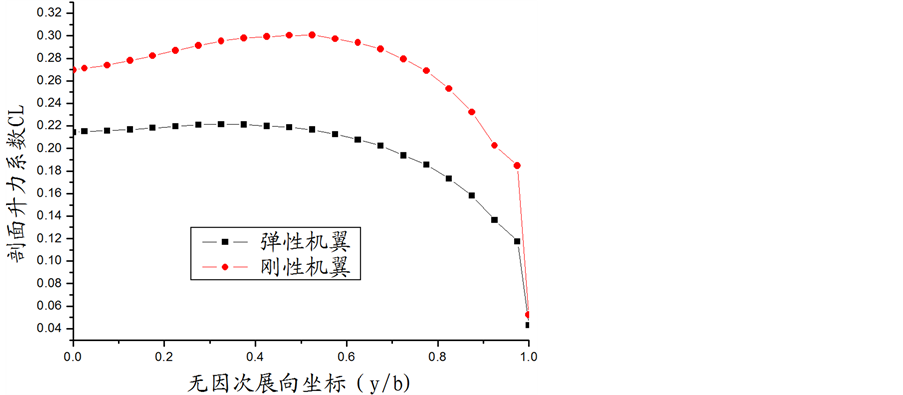
Figure 3. Spanwise distribution of wing lift coefficient
图3. 弹性机翼展向升力系数曲线
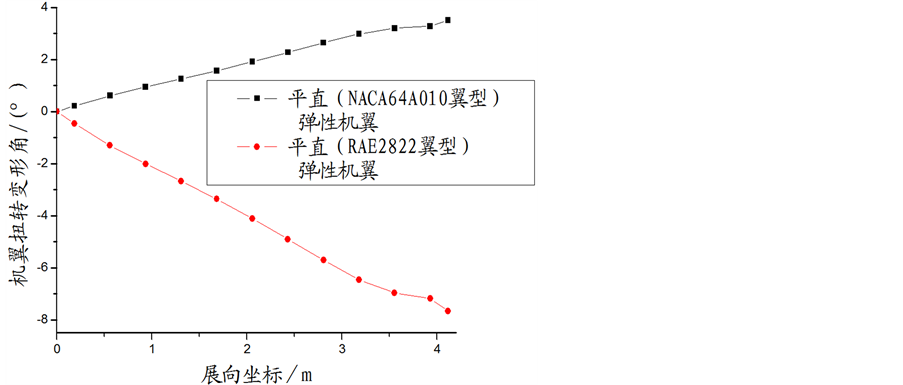
Figure 4. Twist angle distribution of straight elastic wing
图4. 平直弹性机翼展向各剖面的扭转角分布
的机翼抬头变形小于普通翼型机翼。这是因为静气动弹性变形的大小与压力、重心和刚心相对位置有密切关系,一般情况,普通翼型压心靠前,刚心居中,重心在最后,而超临界翼型压心后移,这是导致带超临界翼型的机翼抬头变形小于带普通翼型机翼的主要原因。
5. 结论
1) 中等展弦比后掠机翼气动力和静变形的计算结果与试验和文献对比表明,本文所发展的气动力计
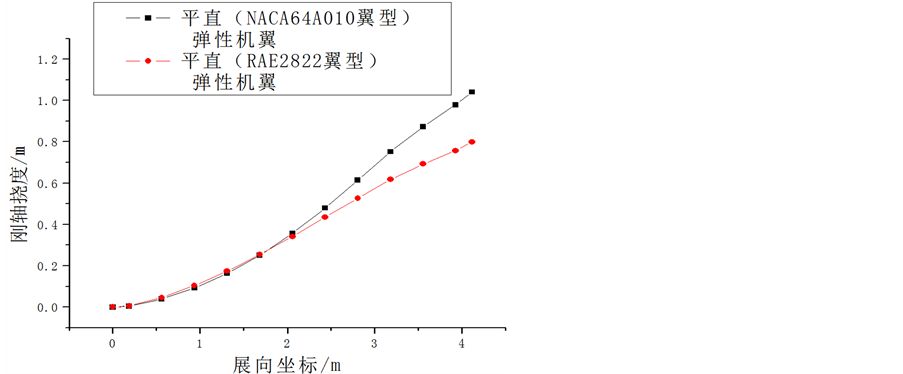
Figure 5. Spanwise deformation distribution of straight elastic in each section wing rigid axis
图5. 平直弹性机翼刚轴展向弹性变形
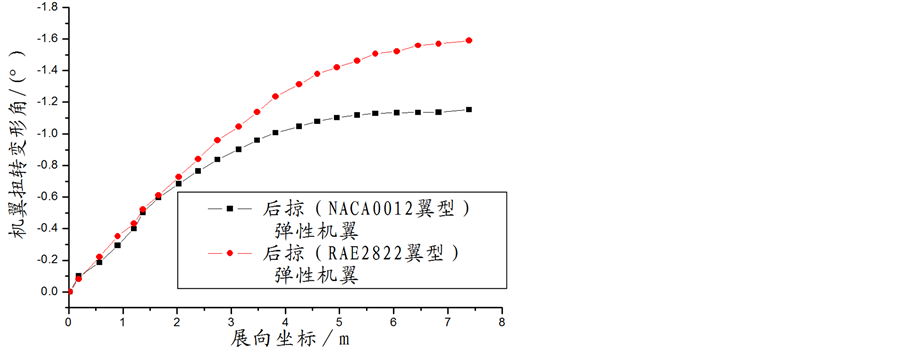
Figure 6. Twist angle distribution of swept elastic wing
图6. 后掠弹性机翼展向各剖面的扭转角分布
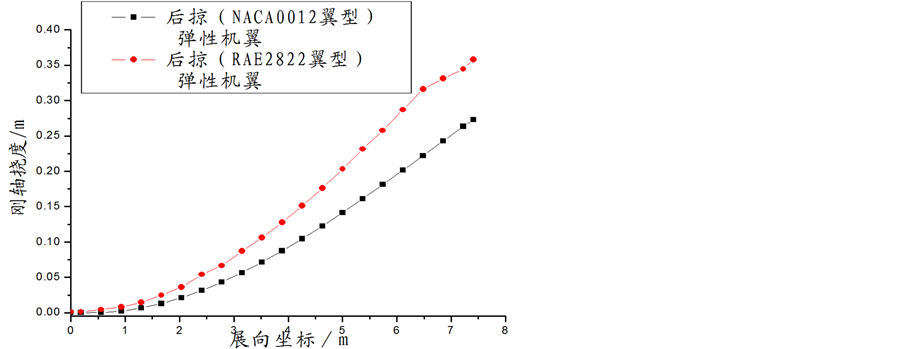
Figure 7. Spanwise deformation distribution of swept elastic in each section wing rigid axis
图7. 后掠弹性机翼刚轴展向弹性变形
算方法比较准确,静变形求解方法比较可靠、效率较高,可以应用到气动–结构一体化设计中。
2) 通过对比超临界机翼和普通机翼的真实弹性变形,总结出了一些超临界机翼静气动弹性变化规律,为超临界机翼的设计、避免静气动弹性的影响从而提高机翼的气动特性提供了理论依据。
基金项目
陕西省科技厅科学研究计划项目(2016JM1030)、陕西理工大学人才启动项目(SLGQD13(2)-21)联合资助。